第7章 特殊关系

等价关系

等价关系概念

等价关系定义：设R是定义在非空集合A上的关系，如果R是自反的、对称的、传递的，则称R为A上的等价关系
同余关系：对于正整数n，考虑整数集合Z上的整除关系\(R=\{<x.y>|x,y\in \textbf{Z}\and (n|(x-y))\}\)，这个关系称为Z上一以n为模的同余关系，一般记为\(x\equiv y(mod n)\)（同余式），同余关系也是等价关系

注意：
由于等价关系有自反性，所以关系内所有序偶的所有元素肯定包含集合A中的元素
这也说明由等价关系对集合A的划分，肯定能对A中的每个元素都指定一个等价类

集合的划分

划分的定义：

对同一个集合，根据不同的划分规则可以得到不同的划分

等价类与商集

等价类：

• 定义：
  
• 性质特点：
  

商集：

• 定义：
  
• 计算\(A/R\)的方法：
  

等价关系与划分

等价关系与集合的划分是一一对应的：

• 等价关系\(\to\)划分：非空集合A上的等价关系R的商集A/R是A的一个划分，该划分称为由R所导出的等价划分
• 划分\(\to\)等价关系：给定集合A的一个划分\(\pi =\{S_{1},S_{2},...,S_{n}\}\)，则由该划分确定的关系\(R=(S_{1}\times S_{1})\cup (S_{2}\times S_{2})\cup ...\cup (S_{n}\times S_{n})\)是A上的等价关系，称该关系由划分\(\pi\)所导出的等价关系

求集合A上的所有不同等价关系即是求集合A的所有不同划分

次序关系

拟序关系

拟序关系：

• 原定义：
  
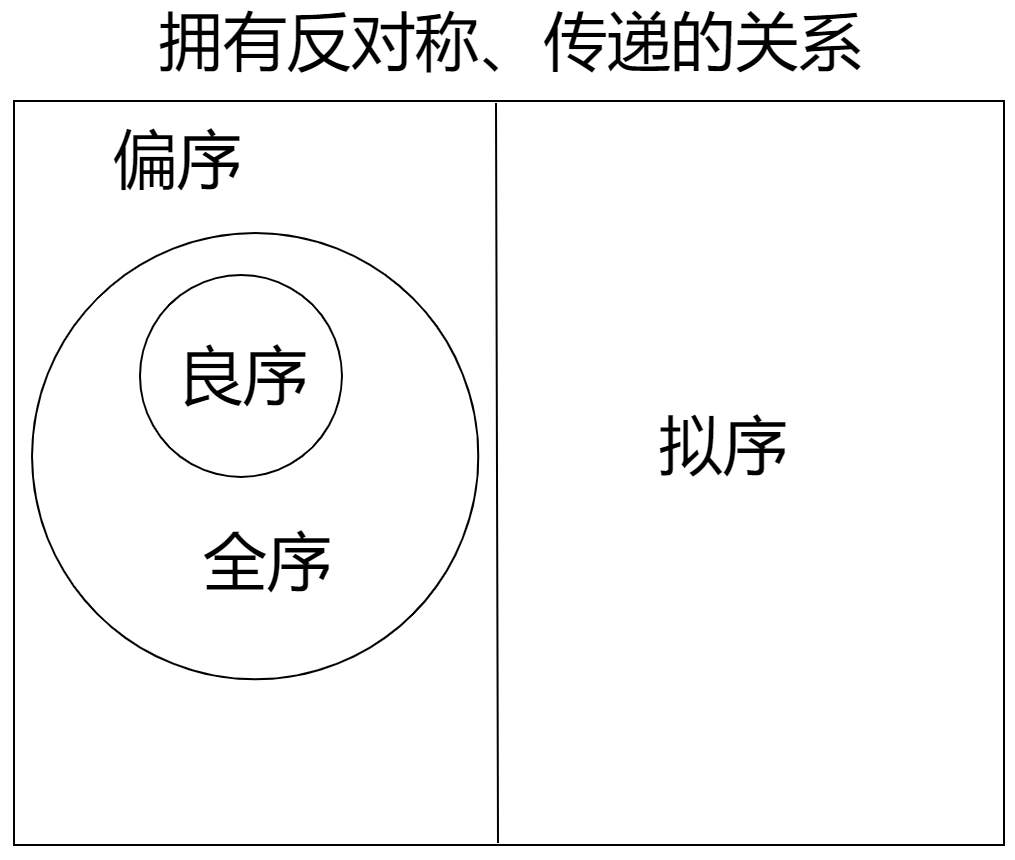
• 简化定义：设R是非空集合A上的关系，如果R是反自反和传递的，则称R是A上的拟序关系

偏序关系

偏序定义

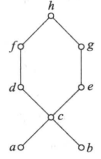
哈斯图定义

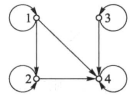
     （关系图）      （哈斯图）

特殊元素

包括有最大元、极大元、最小元、极小元、上界、上确界、下界、下确界

最大元、极大元、最小元、极小元：
设\(<A,\leq>\)是偏序集，\(B\)是\(A\)的一个子集，则有：

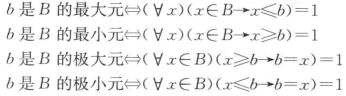
B的最大元，最小元、极大元和极小元如果存在，一定在B中
最大元与极大元的区别：
若\(R=\{<1,1>,<2,2>,<3,3>,<2,1>,<2,3>\}\)，则R的极大元和最大元都是2
若\(R=\{<1,1>,<2,2>,<3,3>,<2,1>,<3,1>\}\)，则R的极大元是2,3无最大元

上界、上确界、下界、下确界：

• 定义：
  
  
• 性质特点：
  

一些例子：

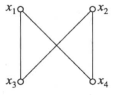
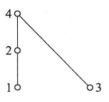
全序关系

全序关系：

• 定义：
  
• 重要性质：当一个偏序关系是全序时，其哈斯图将集合中的元素排成一条线链

例如：
实数集R上的小于或等于关系“\(\leq\)”，是偏序关系，也是全序关系
集合A的幂集\(P(A)\)上的包含关系“\(\subseteq\)”，是偏序关系，但不是全序关系，因为\(\left\{ a\right\}\nsubseteq \left\{ b\right\}\)且\(\left\{ b\right\}\nsubseteq \left\{ a\right\}\)

良序关系

良序关系：

• 定义：设\(<A,\leq>\)是一个偏序集，若A的任何一个非空子集都有最小元，则称“\(\leq\)”为良序关系,简称良序，此时\(<A,\leq>\)称为良序集
• 性质特点：
  • 全序不一定是良序，但良序一定是全序，例如：实数集上的小于等于关系\(\leq\)在(0,1)开区间上没有最小元，所以这个\(\leq\)关系是全序而不是良序
  • 有限全序集一定是良序集

拟序、偏序、全序、良序的关系：