机器学习：决策树

　　对于KNN分类算法，最大的缺点就是无法给出数据的内在含义；而决策树对于数据的划分是一个树状的形式，每次根据一个最能划分数据集的特征来划分数据集，它的主要优势就在于数据形式非常容易理解。

　　以一张图来看一下决策树的形式：

、

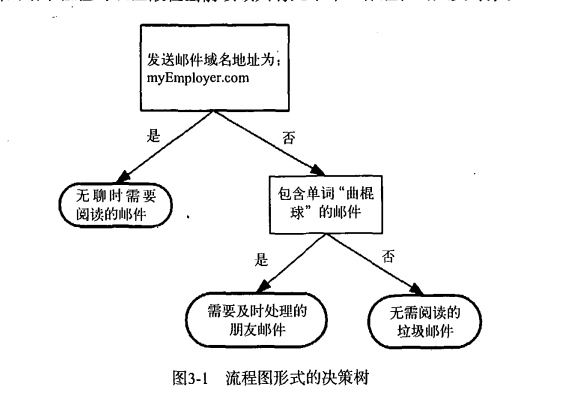
　　由图可以看出，对于每一次划分数据，都找到最能划分数据集的特征，划分之后的两个或几个数据子集，如果数据子集都为相同类的数据，则该子集成为叶子节点，如果数据子集中包含不同类的数据，则继续进行划分，直到达到了停止条件（划分成都为叶子节点或者设置相应的停止条件，后续再说）。

　　决策树很多任务都是为了数据中所蕴含的知识信息，因此决策树可以使用不熟悉的数据集合，并从中提取出一系列规则（数据中所隐含的知识信息），最终这些规则会拿来被使用到实际问题中。由图可以得到这样的规则“邮件域名地址不为myEmployer.com且包含单词‘曲棍球’则是需要及时处理的朋友邮件”。

　　从以上所得知的决策树的构建过程，其中的主要问题是：在每次划分数据集时，如何找到最能划分数据集的特征，这里就引入一个信息增益的概念，通过信息增益的比较来决定每次划分数据集用哪个特征进行划分。

　　信息增益：

　　划分数据集最大的原则就是：将无序的数据变得更加的有序。组织杂乱无章数据的一种方法就是使用信息论度量信息，信息论是量化处理信息的分支科学。可以在划分数据之前使用信息论来量化度量信息的内容。

　　在划分数据集之前之后信息发生的变化被称为信息增益。这样我们计算每个特征划分数据集时的信息增益，获得信息增益最高的特征即为每次划分数据集时最好的选择。

　　信息增益是划分数据集之前之后的信息的变化，对于数据集的当前状态的信息值，我们用信息熵来表示，信息熵的计算公式为：

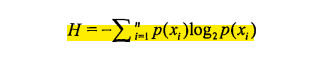
　　其中n表示总共的类别标签个数，xi表示每个类别，p(xi)表示类别xi的数据所占总数据的比例。有了信息熵的计算公式，则可以通过计算差值来得到每个特征划分数据集的信息增益。以下代码为计算信息熵的代码。对于计算信息熵的代码中数据的格式为：[特征1的值，特征2的值，特征3的值，...，特征n的值，类别标签]

from math import log

def calxinXiShang(dataSet):
    num = len(dataSet)
　　# labelCount字典用来存放分类标签和它所对应的数据量。
    lableCount = {}
    for i in range(num):
        currentLabel = dataSet[i][-1]
        if currentLable not in labelCount.keys():
            labelCount[currentLabel] = 0
        labelCount[currentLabel] += 1    
    
    xinXiShang = 0.0
    for label in labelCount.keys():
        prob = float(labelCount[label]) / float(num)
        xinXiShang -= prob * log(prob, 2)
    return xinXiShang

 

　　可以计算信息增益，则可以对数据集进行划分了，首先对于每个特征，要计算出该特征的特征值都有哪些（决策树所针对的数据特征都是标称型数据，因此对于数值型的特征要离散化为标称型），然后计算出每个特征值下的数据子集（数据子集中每个数据项都去掉该属性）的信息熵，将所有特征值的数据子集的信息熵与数据子集所占比例的积累加起来即为使用该特征划分数据的信息熵。则要编写一个对特征的每个特征值提取数据子集的函数，代码如下

def splitDataSet(dataSet, index, value):
    '''
    :param dataSet: 数据集
    :param index: 对该索引的特征求数据子集
    :param value: 求出特征index值为value的数据子集
    :return: 
    '''
    retDataSet = []
    for data in dataSet:
        if data[index] == value:
            # 找到index上值为value的数据，然后去除掉这些数据中的index属性，并将这些数据保存下来
            reduceFeatVec = data[: index]
            reduceFeatVec.extend(data[index + 1:])
            retDataSet.append(reduceFeatVec)

    return retDataSet

　　通过splitDataSet函数可以得到每个特征的每个特征值的数据子集，通过这些数据子集所计算的信息熵与数据子集所占比例的积的和即为使用该特征进行划分数据的信息熵。然后和最初的数据信息熵计算差值即为该特征划分数据集的信息增益。比较每个特征的信息增益得到当前划分数据集的最好的特征，代码如下：

def chooseBestFeature(dataSet):
　　# 首先计算原始的信息熵
    baseXinXiShang = calXinXiShang(dataSet)
    numFeature = len(dataSet[0]) - 1  # 特征的数量
    bestInfoGain = 0.0  # 用来存储最大的信息增益
    bestFeature = -1    # 用来存储获取最大信息增益时所对应的特征
    for i in range(numFeature):
        featValues = []
        # 获得某个特征的所有特征值
        for data in dataSet:
            if data[i] not in featValues:
                featValues.append(data[i])
        currentXinXiShang = 0.0
        for value in featValues:    
            subDataSet = splitDataSet(dataSet, i, value)
            prob = float(len(subDataSet)) / len(dataSet)
            currentXinXiShang += prob * calXinXiShang(subDataSet)       
            currentInfoGain = baseXinXiShang - currentXinXiShang
            if currentInfoGain > bestInfoGain:
                bestInfoGain = currentInfoGain
                bestFeature = i

    return bestFeature

　　有了每次划分数据获取最好特征的方法chooseBestFeature，则可以开始构建决策树了，决策树的构建可以采用递归的原则来处理数据。递归结束的条件是：程序遍历完所有划分数据集的属性，或者每个分支下的所有实例都具有相同的类别。如果所有实例都具有相同的类别，则得到一个叶子节点或者终止块。如果遍历完所有的属性，最后的数据子集中的实例不是同一类，则用数据子集中类别最多的类别作为该子集的类别。获得一个数据集中类别标签最多的类的代码如下：

import operator

def majorLabel(subDataSet):
    labelCount = {}
    for data in subDataSet:
        if data[-1] not in labelCount.keys():
            labelCount[data[-1]] = 0
        labelCount[data[-1]] += 1
    # 以每个分类的数量进行排序（从大到小）
    sortedLabelCount = sorted(labelCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedLabelCount[0][0]

　　决策树的构建，代码如下：