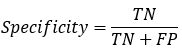机器学习-Confusion Matrix混淆矩阵、ROC、AUC
本文整理了关于机器学习分类问题的评价指标——Confusion Matrix、ROC、AUC的概念以及理解。
混淆矩阵
在机器学习领域中,混淆矩阵(confusion matrix)是一种评价分类模型好坏的形象化展示工具。其中,矩阵的每一列表示的是模型预测的样本情况;矩阵的每一行表示的样本的真实情况。
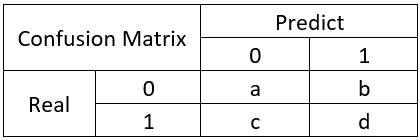
举个经典的二分类例子: 混淆表格:
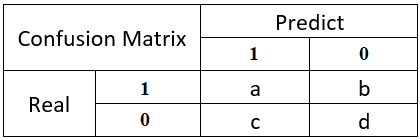

混淆矩阵是除了ROC曲线和AUC之外的另一个判断分类好坏程度的方法,通过混淆矩阵我们可以很清楚的看出每一类样本的识别正误情况。
混淆矩阵比模型的精度的评价指标更能够详细地反映出模型的”好坏”。模型的精度指标,在正负样本数量不均衡的情况下,会出现容易误导的结果。
基本概念
【1】True Positive
真正类(TP),样本的真实类别是正类,并且模型识别的结果也是正类。
【2】False Negative
假负类(FN),样本的真实类别是正类,但是模型将其识别成为负类。
【3】False Positive
假正类(FP),样本的真实类别是负类,但是模型将其识别成为正类。
【4】True Negative
真负类(TN),样本的真实类别是负类,并且模型将其识别成为负类。
评价指标(名词翻译来自机器学习实战)
【1】Accuracy(精确率)
模型的精度,即模型识别正确的个数 / 样本的总个数 。一般情况下,模型的精度越高,说明模型的效果越好。
【2*】Precision(正确率)
又称为查准率,表示在模型识别为正类的样本中,真正为正类的样本所占的比例。 一般情况下,查准率越高,说明模型的效果越好。
关于Accuracy(精确率)和Precision(正确率)的区别:
分类精确率(Accuracy),不管是哪个类别,只要预测正确,其数量都放在分子上,而分母是全部数据数量,这说明精确率是对全部数据的判断。
而正确率在分类中对应的是某个类别,分子是预测该类别正确的数量,分母是预测为该类别的全部数据的数量。
或者说,Accuracy是对分类器整体上的精确率的评价,而Precision是分类器预测为某一个类别的精确率的评价。
【3*】Recall(召回率)=Sensitivity(敏感指标,truepositive rate ,TPR)
=敏感性指标=查全率,表示的是,模型正确识别出为正类的样本的数量占总的正类样本数量的比值。 一般情况下,Recall越高,说明有更多的正类样本被模型预测正确,模型的效果越好。
关于Precision(正确率)和Recall(召回率)的理解,套用网上的一个例子:
某池塘有1400条鲤鱼,300只虾,300只鳖。现在以捕鲤鱼为目的,撒一大网,逮着了700条鲤鱼,200只虾,100只鳖。那么,这些指标分别如下:
正确率 = 700 / (700 +200 + 100) = 70%
召回率 = 700 / 1400 =50%
由此可见,正确率是评估捕获的成果中目标成果所占得比例;召回率,顾名思义,就是从关注领域中,召回目标类别的比例。
正确率和召回率是一对矛盾的度量。以上面这个捕鱼的例子为例,如果希望将鲤鱼尽可能多地捕出来,可以用大网把池塘里的东西都捕出来,那么鲤鱼必然都被捕出来了,但这样正确率会很低。
希望补出的鲤鱼比例尽可能高,那么只捕最有把握的,这样就难免会漏掉一些鲤鱼,使得召回率较低。
通常只有在一些简单任务中,才可能使得正确率和召回率都很高。
【4】Specificity
特异性指标,表示的是模型识别为负类的样本的数量,占总的负类样本数量的比值。
负正类率(false positive rate, FPR),计算公式为:FPR=FP/(TN+FP),计算的是模型错识别为正类的负类样本占所有负类样本的比例,一般越低越好。
Specificity = 1 - FPR
【5】Fβ_Score
Fβ的物理意义就是将正确率和召回率的一种加权平均,在合并的过程中,召回率的权重是正确率的β倍。
F1分数认为召回率和正确率同等重要,
F2分数认为召回率的重要程度是正确率的2倍,更看重recall,即看重模型对正样本的识别能力。
而F0.5分数认为召回率的重要程度是正确率的一半,更看重precision,即看重模型对负样本的区分能力。
分类阈值对Precision/Recall的影响:
做二值分类时(predict为1则为positive),我们认为,若h(x)>=0.5,则predict=1;若h(x)<0.5,则predict=0。这里0.5就是分类阈值。
增加阈值,我们会对预测值更有信心,即增加了查准率。但这样会降低查全率。(High Precision, Low Recall)
减小阈值,则模型放过的真例就变少,查全率就增加。(Low Precision, High Recall)
实际应用:
(1)如果是做搜索,则要在保证召回率理想的情况下,提升准确率;
(2)如果做疾病监测、反垃圾,则是要保证准确率的条件下,提升召回率。
对于predict与recall:一句话,准确率就是“找的对”,召回率就是“找的全”。
比较常用的是F1分数(F1 Score),是统计学中用来衡量二分类模型精确度的一种指标。
【6】F1_Score
数学定义:F1分数(F1_Score),又称为平衡F分数(BalancedScore),它被定义为正确率和召回率的调和平均数。
β=1的情况,F1-Score的值是从0到1的,1是最好,0是最差。
回到上面二分类的例子:
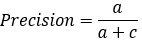
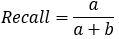
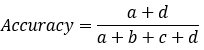
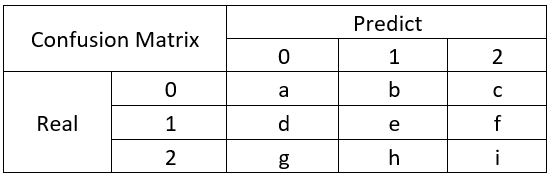
那么多分类呢?
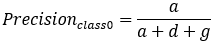
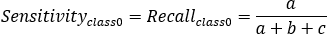
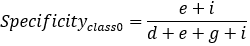
因此我们知道,计算Precision,Recall,Specificity等只是计算某一分类的特性,而Accuracy和F1-Score是判断分类模型总体的标准。
sklearn中 F1-micro 与 F1-macro区别和计算原理
在sklearn中的计算F1的函数为 f1_score ,其中有一个参数average用来控制F1的计算方式,今天我们就说说当参数取micro和macro时候的区别。
'micro':Calculate metrics globally by counting the total true positives, false negatives and false positives.'micro':通过先计算总体的TP,FN和FP的数量,再计算F1
'macro':Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.'macro':分布计算每个类别的F1,然后做平均(各类别F1的权重相同)
详见:https://www.cnblogs.com/techengin/p/8962024.html
ROC曲线
ROC曲线的横坐标是前文提到的FPR(false positive rate),纵坐标是TPR(true positive rate,召回率)。
放在具体领域来理解上述两个指标。如在医学诊断中,判断有病的样本。
- 那么尽量把有病的揪出来是主要任务,也就是第二个指标TPR,要越高越好。
- 而把没病的样本误诊为有病的,也就是第一个指标FPR,要越低越好。
不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的第一个指标应该会很高,但是第二个指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么第一个指标达到1,第二个指标也为1。
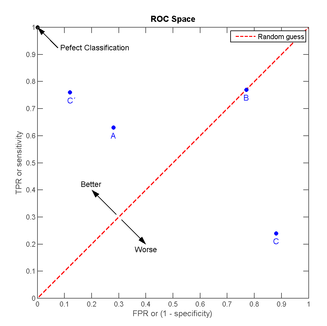
我们可以看出
- 左上角的点(TPR=1,FPR=0),为完美分类,也就是这个医生医术高明,诊断全对。
- 点A(TPR>FPR),医生A的判断大体是正确的。中线上的点B(TPR=FPR),也就是医生B全都是蒙的,蒙对一半,蒙错一半;下半平面的点C(TPR<FPR),这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医。
- 曲线距离左上角越近,证明分类器效果越好。
为什么使用ROC曲线
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?
因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
AUC值
AUC(Area Under Curve)被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
- AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
计算AUC:
- 第一种方法:AUC为ROC曲线下的面积,那我们直接计算面积可得。面积为一个个小的梯形面积之和。计算的精度与阈值的精度有关。
- 第二种方法:根据AUC的物理意义,我们计算正样本score大于负样本的score的概率。取N*M(N为正样本数,M为负样本数)个二元组,比较score,最后得到AUC。时间复杂度为O(N*M)。
- 第三种方法:与第二种方法相似,直接计算正样本score大于负样本的概率。我们首先把所有样本按照score排序,依次用rank表示他们,如最大score的样本,rank=n(n=N+M),其次为n-1。那么对于正样本中rank最大的样本,rank_max,有M-1个其他正样本比他score小,那么就有(rank_max-1)-(M-1)个负样本比他score小。其次为(rank_second-1)-(M-2)。最后我们得到正样本大于负样本的概率为