机器学习基础

贝叶斯公式理解：

例子可以看知乎高票：https://www.zhihu.com/question/19725590

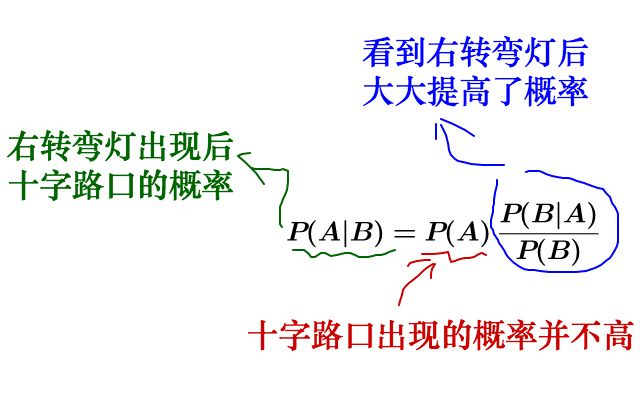
可以理解为：

                                                                          后验概率　＝　先验概率 ｘ 调整因子

我们把P(A)称为"先验概率"（Prior probability），即在B事件发生之前，我们对A事件概率的一个判断。

P(A|B)称为"后验概率"（Posterior probability），即在B事件发生之后，我们对A事件概率的重新评估。

P(B|A)/P(B)称为"可能性函数"（Likelyhood），这是一个调整因子，使得预估概率更接近真实概率。

贝叶斯推断的含义：我们先预估一个"先验概率"，然后加入实验结果，看这个实验到底是增强还是削弱了"先验概率"，由此得到更接近事实的"后验概率"。通过大量数据去修正。

 

K-means 

转自：https://zhuanlan.zhihu.com/p/20432322

　　　https://coolshell.cn/articles/7779.html

可视化：http://stanford.edu/class/ee103/visualizations/kmeans/kmeans.html

1）K-Means算法的特点是类别的个数是人为给定的，如果让机器自己去找类别的个数，我们有AP聚类算法，先不说，说了就跑题了。
K-Means的一个重要的假设是：数据之间的相似度可以使用欧氏距离度量，如果不能使用欧氏距离度量，要先把数据转换到能用欧氏距离度量，这一点很重要。
（注：可以使用欧氏距离度量的意思就是欧氏距离越小，两个数据相似度越高）

 

2）二维坐标点的X, Y 坐标，其实是一种向量，是一种数学抽象。

现实世界中很多属性是可以抽象成向量的，比如，我们的年龄，我们的喜好，我们的商品，等等，能抽象成向量的目的就是可以让计算机知道某两个属性间的距离。

如：我们认为，18岁的人离24岁的人的距离要比离12岁的距离要近，鞋子这个商品离衣服这个商品的距离要比电脑要近，等等。

只要能把现实世界的物体的属性抽象成向量，就可以用K-Means算法来归类了。

在 《k均值聚类(K-means)》 这篇文章中举了一个很不错的应用例子，作者用亚洲15支足球队的2005年到1010年的战绩做了一个向量表，然后用K-Means把球队归类，得出了下面的结果。

• 亚洲一流：日本，韩国，伊朗，沙特
• 亚洲二流：乌兹别克斯坦，巴林，朝鲜
• 亚洲三流：中国，伊拉克，卡塔尔，阿联酋，泰国，越南，阿曼，印尼

其实，这样的业务例子还有很多，比如，分析一个公司的客户分类，这样可以对不同的客户使用不同的商业策略，或是电子商务中分析商品相似度，归类商品，从而可以使用一些不同的销售策略，等等。

标准差（Standard Deviation）

中文环境中又常称均方差，是离均差平方的算术平均数的平方根，用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。