poj 2488 A Knight's Journey(dfs)

Description

Background 
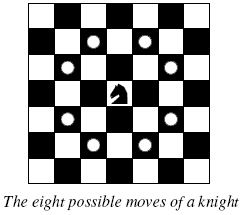
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

描述：就是从p行q列的棋盘上的某一点出发，列用A，B……表示，行用1，2，3……表示。然后每次只能走“日”字，和象棋中的马一样，问能不能在不重复的情况下遍历棋盘。能的话就按字典序输出遍历的路径，其中输出格式为先列后行，不能的话就输出impossible。

 

解析：既然遍历该棋盘，并且按字典序输出。那就从最左上角A1开始进行DFS遍历。要注意的是按字典序输出，所以遍历时的顺序很重要，按从上到下，从左到右的顺序遍历。

 

Java AC代码

import java.util.Scanner;

public class Main {

    static Point path[];               //记录遍历路径
    
    static boolean[][] marked;         //访问过则为true，未访问过则为false
    
    static int dx[] = {-2, -2, -1, -1, 1, 1, 2, 2};       //八个方向的列值的变化
    static int dy[] = {-1, 1, -2, 2, -2, 2, -1, 1};       //八个方向的行值的变化
    
    static int p,q;
    
    public static boolean dfs(int row, int col, int step) {       
        
        marked[row][col] = true;                               
        path[step] = new Point(row, col); //第step步 访问的是（row,col）这个点
        
        if(step == p * q)         //递归出口，因为一共只有p*q个点，当访问步数等于p*q时，说明所有点都已经访问过了，找到了结果，返回true
            return true;
            
        for(int i = 0; i < 8; i++) {
            int _col = col + dx[i];                   
            int _row = row + dy[i];
            if(_row >=1 && _row <= p && _col >=1 && _col <=q && !marked[_row][_col]) { 
                if(dfs(_row, _col, step + 1)) 
                    return true;
            }
        }
        
        marked[row][col] = false; //到这说明从(row,col)这个点出去的深搜都失败了，所以访问位设置为false,返回上一个点进行其他的深搜
        return false;
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int input[] = new int[2 * n + 1]; //把输入的数都保存在数组里
        int cases = 0;
        int index = 1;
        
        for(int i = 1; i <= 2 * n; i++) {
            input[i] = sc.nextInt();
        }
        
        while(n > 0) {
            marked = new boolean[27][27];
            p = input[index];   
            q = input[index + 1];
            path = new Point[p * q + 1];
            cases++;
            System.out.println("Scenario #" + cases + ":");
            boolean flag = dfs(1, 1, 1);
                
            if(flag) {   //成功遍历时的输出
                for(int i = 1; i <= p * q; i++) {
                    System.out.print((char)(path[i].column - 1 + 'A'));
                    System.out.print(path[i].row);
                }
                System.out.print("\n");
            } else {    //失败的输出
                System.out.println("impossible");
            }
            
            if(n != 0)
                System.out.print("\n");
            n--;
            index = index + 2;
        }
    }
}

class Point {
    public int row;
    public int column;
    
    public Point(int row, int column) {
        this.row = row;
        this.column = column;
    }
}