哈弗曼编码
前言：
众所周知，生活中许多方面都需要编码。而在字符的存储中，编码方式一般分为等长编码和不等长编码两种。
1 等长编码：00 01 11 2 不等长编码：00 01 010 0111
等长编码由于所有字符编码长度相等，所以n个不同字符需[logn]位编码。
而不等长编码中，使用频率高的字符编码长度短，使用频率低的字符编码长度长。
因此，为达到最优的使编码总长度最短的编码方案，不等长编码应解决两个问题：
1.编码尽可能短；
2.不能有二义性（即一个字符的编码不能为另一字符编码的前缀，因为会产生歧义）。
1 二义性示例： 2 a：01 b：010 c：10010 3 01010010：abb、bc
所以，就有了哈夫曼编码的编码方式~
哈弗曼编码详解：
首先，哈夫曼编码以字符的使用频率为基础编码，频率越高，编码越短；且以频数大小建树，频数越小，离根越远。
在需编码的n个字符的中，以字符为叶子节点，以频数为叶子的权值，通过n-1次合并，自下而上构造哈夫曼树。其核心思想是权值大的叶子离根近。
具体思路：每次在树的集合中选取两个无父亲的不同的权值最小的树作为左右子树，构造一棵新树，通向左子树的边权为0，通向右子树的边权为1，其根的权值为左右子树权值之和，再次插入树的集合。
以下列表、画图讲解（十分粗糙，将就一下）：
| 字符 | a | b | c | d | e |
| 频数 | 0.05 | 0.32 | 0.18 | 0.07 | 0.25 |
在上表中，n=5，共合并n-1=4次。
第一次：选取a、d作为左右子树，新树权值为0.12，设新树为A，将a、d删除，插入新节点A，新表格如下：
| 字符 | a（删） | b | c | d（删） | e | A |
| 频数 | 0.05 | 0.32 | 0.18 | 0.07 | 0.25 | 0.12 |
图：
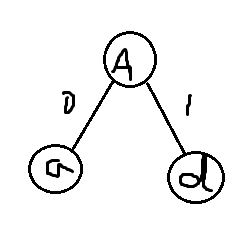
第二次：选取A、c作为左右子树，新树权值为0.30，设新树为B，将A、c删除，插入新节点B，新表格如下：
| 字符 | a（删） | b | c（删） | d（删） | e | A（删） | B |
| 频数 | 0.05 | 0.32 | 0.18 | 0.07 | 0.25 | 0.12 | 0.30 |
图：
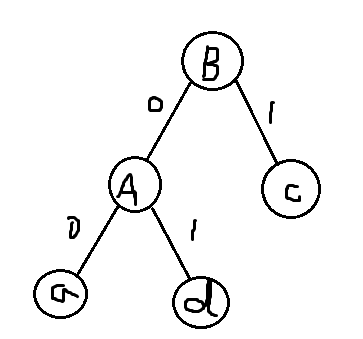
第三次：选取e、B作为左右子树，新树权值为0.55，设新树为C，将e、B删除，插入新节点C，新表格如下：
| 字符 | a（删） | b | c（删） | d（删） | e（删） | A（删） | B（删） | C |
| 频数 | 0.05 | 0.32 | 0.18 | 0.07 | 0.25 | 0.12 | 0.30 | 0.55 |
图：
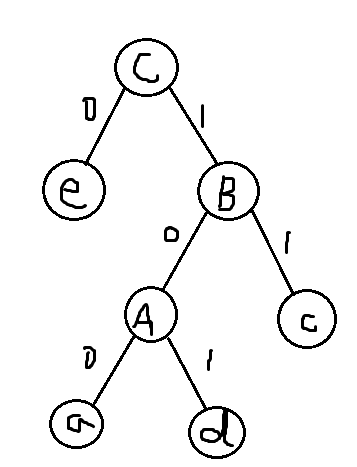
第四次：选取b、C作为左右子树，新树权值为0.87，设新树为D，将b、C删除，插入新节点D，新表格如下：
| 字符 | a（删） | b（删） | c（删） | d（删） | e（删） | A（删） | B（删） | C（删） | D |
| 频数 | 0.05 | 0.32 | 0.18 | 0.07 | 0.25 | 0.12 | 0.30 | 0.55 | 0.87 |
图：
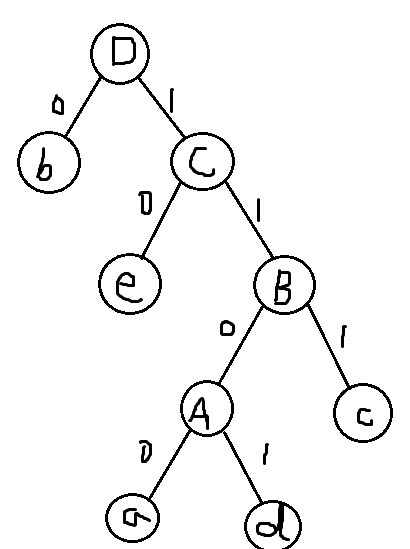
则D为该树的根，看图写出a、b、c、d、e的编码如下：
a：1100； b：0； c：111； d：1101； e：10
可见，频数越大，编码越短，且比等长编码所需内存小，因此大受欢迎（五笔输入法就是这个原理~）
接下来进入代码实现阶段（^_^）~
代码实现：
首先，还是定义一个n表示字符个数~
再定义一个结构体，用于记录字符的权值、父亲、左右儿子和01编码。
1 int n;//需要建成哈夫曼树的数的个数 2 3 struct k1{//哈夫曼树节点结构体 4 int w=0;//编码（从该节点到其父亲节点的边的权值） 5 int fa=-1;//父亲 6 int lc=-1,rc=-1;//左右儿子 7 int t;//他自己的值 8 }e[105];//数组爱开多大开多大（别超内存限制）
再再定义一个结构体，用于存储字符的编码。
1 struct k2{//编码结构体 2 int bits[105];//码 3 int start=0;//长度 4 }data[105];
然后写好框架后，在主函数中输入。
1 cin >> n;//输入 2 for(int i=1; i<=n; i++)//输入（我很闲） 3 { 4 int a; 5 cin >> a;//输入 6 e[i].t = a;//赋值（完全可以直接输入e[i].t，但我就这么写） 7 }
因为要合并n-1次，所以循环从n-1开始到2n-1结束。循环中就是讲解中的具体思路啦~
1 int m=2*n-1;//共n个数，需合并n-1次，再加n为2n-1 2 for(int i=n+1; i<=m; i++)//从n+1到2n-1为父亲节点（1到n也有可能） 3 { 4 int t1,t2;//无父亲的下标不重复的两个最小数 5 Select(i-1,t1,t2);//因为e[i]为父亲节点，所以左右儿子从1到i-1中找 6 cout << t1 << " " << t2 << endl;//测试代码（不用写） 7 e[t1].fa = e[t2].fa = i;//下标为t1，t2的两个无父亲下标不相同最小数的父亲相同 8 e[t2].w = 1;//右儿子编码为1 9 e[i].lc = t1;//父亲节点的左儿子下标 10 e[i].rc = t2;//父亲节点的右儿子下标 11 e[i].t = e[t1].t + e[t2].t;//父亲节点的值为左右儿子值的和 12 }
这个Select函数是选最小值的。
1 void Select(int nn,int &t1,int &t2)//找无父亲的下标不重复的两个最小数 2 { 3 int min;//先给最个小数 4 for(int i=1; i<=nn; i++)//先找无父亲的数 5 { 6 if(e[i].fa==-1)//无父亲 7 { 8 min = i; 9 break;//赋值后跳出循环 10 } 11 }//这个循环先给min付个值 12 for(int j=1; j<=nn; j++)//再找无父亲的数 13 { 14 if(e[j].fa==-1)//无父亲 15 { 16 if(e[j].t<e[min].t) min = j;//比较下谁最小，赋值 17 } 18 } 19 t1 = min;//t1为无父亲的最小数 20 for(int i=1; i<=nn; i++)//再找无父亲的数 21 { 22 if(e[i].fa==-1 && i!=t1)//无父亲且下标不与t1相同 23 { 24 min = i; 25 break;//赋值后跳出循环 26 } 27 } 28 for(int j=1; j<=nn; j++)//继续找无父亲的数 29 { 30 if(e[j].fa==-1 && j!=t1)//无父亲且下标不与t1相同 31 { 32 if(e[j].t<e[min].t) min = j;//再比较下谁第二小，赋值 33 } 34 } 35 t2 = min;//t2为无父亲的下标不与t1相等的第二小的数 36 }
如果不习惯&t1，也可以将t1、t2定义为全局变量，函数中可直接调用，无需定义~
平平无奇的输出。
1 for(int i=1; i<=m; i++)//输出 2 { 3 cout << e[i].fa << " " << e[i].lc << " " << e[i].rc << " " << e[i].t << " " << e[i].w << endl; 4 }
计算编码。
1 for(int i=1; i<=n; i++)//计算编码 2 { 3 bianma(i); 4 }
计算编码的函数如下：
1 void bianma(int a)//计算编码 2 { 3 data[a].bits[data[a].start+1] = e[a].w;//如果要算根节点的话要加，这里可以不加 4 data[a].start++;//很正常的加1 5 int i=a;//定义变量i从a开始反向找编码 6 while(i!=-1)//若到了根节点则退出 7 { 8 i = e[i].fa;//找父亲 9 data[a].bits[data[a].start+1] = e[i].w;//bits数组记录编码 10 data[a].start++;//还是很正常的加1 11 } 12 }
最后，输出编码。
for(int i=1; i<=n; i++)//输出编码 { for(int j=data[i].start-2; j>=1; j--)//因为每个节点都有01编码，所以边的编码应减去最后两个（如果想按节点算可以不减2） { cout << data[i].bits[j]; } cout << endl; }
完整（不删测试代码的）代码：
1 #include<iostream> 2 #include<algorithm> 3 #include<queue> 4 #include<cstring> 5 #include<string> 6 7 using namespace std; 8 9 int n;//需要建成哈夫曼树的数的个数 10 //long long int minn; 11 //int data[20005]; 12 13 struct k1{//哈夫曼树节点结构体 14 int w=0;//编码（从该节点到其父亲节点的边的权值） 15 int fa=-1;//父亲 16 int lc=-1,rc=-1;//左右儿子 17 int t;//他自己的值 18 }e[105];//数组爱开多大开多大（别超内存限制） 19 20 struct k2{//编码结构体 21 int bits[105];//码 22 int start=0;//长度 23 }data[105]; 24 25 //priority_queue<int,vector<int>,greater<int>>k; 26 27 //int temp1=-1,temp2=-1; 28 29 void Select(int nn,int &t1,int &t2)//找无父亲的下标不重复的两个最小数 30 { 31 int min;//先给最个小数 32 // cout << "dfgdfg"; 33 for(int i=1; i<=nn; i++)//先找无父亲的数 34 { 35 if(e[i].fa==-1)//无父亲 36 { 37 min = i; 38 break;//赋值后跳出循环 39 } 40 }//这个循环先给min付个值 41 for(int j=1; j<=nn; j++)//再找无父亲的数 42 { 43 if(e[j].fa==-1)//无父亲 44 { 45 if(e[j].t<e[min].t) min = j;//比较下谁最小，赋值 46 } 47 } 48 t1 = min;//t1为无父亲的最小数 49 // cout << t1 << " "; 50 for(int i=1; i<=nn; i++)//再找无父亲的数 51 { 52 if(e[i].fa==-1 && i!=t1)//无父亲且下标不与t1相同 53 { 54 min = i; 55 // cout << i << endl; 56 break;//赋值后跳出循环 57 } 58 } 59 for(int j=1; j<=nn; j++)//继续找无父亲的数 60 { 61 if(e[j].fa==-1 && j!=t1)//无父亲且下标不与t1相同 62 { 63 if(e[j].t<e[min].t) min = j;//再比较下谁第二小，赋值 64 } 65 } 66 t2 = min;//t2为无父亲的下标不与t1相等的第二小的数 67 // cout << t2 << endl; 68 } 69 70 void bianma(int a)//计算编码 71 { 72 data[a].bits[data[a].start+1] = e[a].w;//如果要算根节点的话要加，这里可以不加 73 data[a].start++;//很正常的加1 74 int i=a;//定义变量i从a开始反向找编码 75 // cout << a << " : "; 76 while(i!=-1)//若到了根节点则退出 77 { 78 i = e[i].fa;//找父亲 79 // cout << i << " "; 80 data[a].bits[data[a].start+1] = e[i].w;//bits数组记录编码 81 data[a].start++;//还是很正常的加1 82 // cout << data[a].start << " "; 83 } 84 // cout << endl; 85 } 86 87 int main() 88 { 89 cin >> n;//输入 90 for(int i=1; i<=n; i++)//输入（我很闲） 91 { 92 int a; 93 cin >> a;//输入 94 e[i].t = a;//赋值（完全可以直接输入e[i].t，但我就这么写） 95 } 96 int m=2*n-1;//共n个数，需合并n-1次，再加n为2n-1 97 // int temp=1; 98 for(int i=n+1; i<=m; i++)//从n+1到2n-1为父亲节点（1到n也有可能） 99 { 100 int t1,t2;//无父亲的下标不重复的两个最小数 101 102 Select(i-1,t1,t2);//因为e[i]为父亲节点，所以左右儿子从1到i-1中找 103 cout << t1 << " " << t2 << endl;//测试代码（不用写） 104 e[t1].fa = e[t2].fa = i;//下标为t1，t2的两个无父亲下标不相同最小数的父亲相同 105 e[t2].w = 1;//右儿子编码为1 106 e[i].lc = t1;//父亲节点的左儿子下标 107 e[i].rc = t2;//父亲节点的右儿子下标 108 e[i].t = e[t1].t + e[t2].t;//父亲节点的值为左右儿子值的和 109 } 110 for(int i=1; i<=m; i++)//输出 111 { 112 cout << e[i].fa << " " << e[i].lc << " " << e[i].rc << " " << e[i].t << " " << e[i].w << endl; 113 } 114 for(int i=1; i<=n; i++)//计算编码 115 { 116 bianma(i); 117 } 118 for(int i=1; i<=n; i++)//输出编码 119 { 120 // for(int j=data[i].start; j>=1; j--) 121 // for(int j=1; j<=data[i].start; j++) 122 for(int j=data[i].start-2; j>=1; j--)//因为每个节点都有01编码，所以边的编码应减去最后两个（如果想按节点算可以不减2） 123 { 124 cout << data[i].bits[j]; 125 } 126 cout << endl; 127 } 128 return 0; 129 }
其实还有一种用优先队列写的方法，下面讲可变基哈夫曼树时会使用这个方法，所以这里就不讲了（^_^）
虽然哈夫曼树编码占用内存小，但架不住字符多呀！当需编码字符太多时，往往也采用可变基哈夫曼树来编码。
下面有请可变基哈夫曼树~
可变基哈夫曼树详解：
哈夫曼树就是每个根节点只有左右两个儿子，而可变基哈夫曼树不同。如果基数为3，则有左中右三个儿子；如果基数为4，这有左，中间靠左，中间靠右，右四个儿子……以此类推，当基数为n时，一个根节点有n个儿子，这就很好的解决了字符太多时，普通的哈弗曼树编码过长的问题。
下面就不列表画图详解了哈，原理都一样，只是基数不同。
直接讲代码：
首先同上，定义n、结构体（我太懒了，不想再搞一遍编码，所以本次代码没有编码结构体更没有编码函数更更没有输出编码！！！）
此处还要有基数，n用gs代替，代码都有详细注释，我就不再写一遍啦~
1 struct k1{ 2 int freq,va,id;//频率，优先值，编号 3 k1(int x=0,int y=0, int z=0)//全部赋值为零 4 { 5 freq = x;//赋值 6 va = y;//赋值 7 id = z;//赋值 8 } 9 bool operator <(const k1 &b) const{//排序函数 10 if(freq==b.freq) return va>b.va;//若频率相同，就以优先值小的先 11 return freq>b.freq;//否则频率小的先 12 } 13 }; 14 15 int js,zm;//基数（就是二叉树、三叉树、N叉树的决定数），字母数 16 int gs,bh;//补虚拟字母后的字母数，编号 17 int pl[105],fa[105],code[105];//频率，父节点，编码 18 priority_queue<k1>k;//k1类型的优先队列
至于优先队列，好处是不用排序，所以更方便哟~
继续:
1 int main() 2 { 3 int cas=1;//记录输入了几组数据 4 while(cin >> js && js)//输入基数并判断基数大于零 5 { 6 cin >> zm;//输入字母数 7 memset(pl,0,sizeof(pl));//频率数组刷新为0（因为要多次使用） 8 int total=0;//记录所有频率和 9 for(int i=1; i<=zm; i++)//输入频率 10 { 11 cin >> pl[i]; 12 total+=pl[i];//计算频率和 13 } 14 gs = zm;//将需补数的字母数赋值为实际字母数 15 while((gs-js)%(js-1))//k（js-1）+js=gs，所以加到满足为止 16 { 17 gs++; 18 } 19 while(!k.empty())//将队列清空 20 { 21 k.pop(); 22 } 23 for(int i=1; i<=gs; i++)//队列中加入新值 24 { 25 k.push(k1(pl[i],i,i)); 26 } 27 bh = gs+1;//因为我是从1开始输入，所以数组再赋新值要加1；从0开始不用 28 int rec=0;//记录所有频率 29 while(k.size()!=1)//队列不为1，循环不停 30 { 31 int sum=0,minva=gs;//记录一次while循环中字母的频率 32 for(int i=1; i<=js; i++)//循环基数次 33 { 34 sum+=k.top().freq;//加上频率 35 minva = min(minva,k.top ().va);//选出最小优先值 36 fa[k.top().id] = bh;//k.top()的父亲为bh 37 code[k.top().id] = i;//k.top()的编码为i 38 k.pop();//最小值出队 39 } 40 k.push(k1(sum,minva,bh));//新节点入队 41 pl[bh] = sum;//频率数组的第bh个赋值为sum 42 bh++;//编号+1 43 rec+=sum;//rec加频率 44 } 45 bh--;//编号由于循环中+1，此处-1 46 code[bh] = 1;//编码数组第bh个为根，一定为1；若从0开始则一定为0 47 for(int i=1; i<=bh; i++)//输出 48 { 49 // kk a=k.top(); 50 // cout << k.top().freq << " " << k.top().va << " " << k.top().id << endl; 51 cout << pl[i] << " " << fa[i] << " " << code[i] << endl; 52 } 53 cas++;//开始第二个循环 54 } 55 return 0; 56 }
其他大家自己看吧，都有注释。
完整版更方便看哦~
1 #include<iostream> 2 #include<algorithm> 3 #include<queue> 4 #include<cstring> 5 #include<string> 6 7 using namespace std; 8 9 struct k1{ 10 int freq,va,id;//频率，优先值，编号 11 k1(int x=0,int y=0, int z=0)//全部赋值为零 12 { 13 freq = x;//赋值 14 va = y;//赋值 15 id = z;//赋值 16 } 17 bool operator <(const k1 &b) const{//排序函数 18 if(freq==b.freq) return va>b.va;//若频率相同，就以优先值小的先 19 return freq>b.freq;//否则频率小的先 20 } 21 }; 22 23 int js,zm;//基数（就是二叉树、三叉树、N叉树的决定数），字母数 24 int gs,bh;//补虚拟字母后的字母数，编号 25 int pl[105],fa[105],code[105];//频率，父节点，编码 26 priority_queue<k1>k;//k1类型的优先队列 27 28 //struct k2{ 29 // int fa; 30 // int lc,rc; 31 // int t; 32 //}e[20005]; 33 34 //priority_queue<int,vector<int>,greater<int>>k; 35 36 int main() 37 { 38 int cas=1;//记录输入了几组数据 39 while(cin >> js && js)//输入基数并判断基数大于零 40 { 41 cin >> zm;//输入字母数 42 memset(pl,0,sizeof(pl));//频率数组刷新为0（因为要多次使用） 43 int total=0;//记录所有频率和 44 for(int i=1; i<=zm; i++)//输入频率 45 { 46 cin >> pl[i]; 47 total+=pl[i];//计算频率和 48 } 49 gs = zm;//将需补数的字母数赋值为实际字母数 50 while((gs-js)%(js-1))//k（js-1）+js=gs，所以加到满足为止 51 { 52 gs++; 53 } 54 while(!k.empty())//将队列清空 55 { 56 k.pop(); 57 } 58 for(int i=1; i<=gs; i++)//队列中加入新值 59 { 60 k.push(k1(pl[i],i,i)); 61 } 62 bh = gs+1;//因为我是从1开始输入，所以数组再赋新值要加1；从0开始不用 63 int rec=0;//记录所有频率 64 while(k.size()!=1)//队列不为1，循环不停 65 { 66 int sum=0,minva=gs;//记录一次while循环中字母的频率 67 for(int i=1; i<=js; i++)//循环基数次 68 { 69 sum+=k.top().freq;//加上频率 70 minva = min(minva,k.top ().va);//选出最小优先值 71 fa[k.top().id] = bh;//k.top()的父亲为bh 72 code[k.top().id] = i;//k.top()的编码为i 73 k.pop();//最小值出队 74 } 75 k.push(k1(sum,minva,bh));//新节点入队 76 pl[bh] = sum;//频率数组的第bh个赋值为sum 77 bh++;//编号+1 78 rec+=sum;//rec加频率 79 } 80 bh--;//编号由于循环中+1，此处-1 81 code[bh] = 1;//编码数组第bh个为根，一定为1；若从0开始则一定为0 82 for(int i=1; i<=bh; i++)//输出 83 { 84 // kk a=k.top(); 85 // cout << k.top().freq << " " << k.top().va << " " << k.top().id << endl; 86 cout << pl[i] << " " << fa[i] << " " << code[i] << endl; 87 } 88 cas++;//开始第二个循环 89 } 90 return 0; 91 }
讲解就结束啦，然后是练习题，不要跳过哦~
练习：https://vjudge.net/problem/POJ-3253#author=boboyang
这个练习其实比纯算法简单，因为算法中的很多东西都不需要，认真考虑很快就能写出来，所以就偷懒浅讲一下~
因为题目要求合并所有果子的最小代价，如果按照样例画图的话会发现就是所有父亲节点的权值的和，别的都不需要。那索性直接用优先队列累加最小值，最后输出就好啦~
代码：
1 #include<iostream> 2 #include<algorithm> 3 #include<queue> 4 5 using namespace std; 6 7 int n;//共有n堆果子待合并 8 long long int minn;//这里一定要仔细，题目中每堆果子最多有500000个，而n最多有2000堆，所以合理推测合并所有果子的最小代价最大会超过int类型的最大值 9 int data[20005];//超最大值几个我比较放心 10 11 //struct kk{ 12 // int fa; 13 // int lc,rc; 14 // int t; 15 //}e[20005]; 16 17 priority_queue<int,vector<int>,greater<int>>k;//用优先队列存储合并果子的代价（还不用排序） 18 19 int main() 20 { 21 cin >> n;//输入 22 for(int i=1; i<=n; i++)//输入 23 { 24 int a;//定义变量记录合并第i堆果子的代价 25 cin >> a;//输入 26 k.push(a);//因为是优先队列，所以只能这么输入 27 } 28 // sort(data,data+n+1); 29 30 while(k.size()>1)//当队列中只有一个数时，表明合并果子的代价全部累加完 31 { 32 int x=k.top();//第一个最小代价 33 k.pop();//出队 34 int y=k.top();//第二个最小代价 35 k.pop();//出队 36 minn = minn + x + y;//代价之和 37 k.push(x+y);//代价之和再次入队 38 } 39 // cout << minn; 40 /* 41 for(int i=1; i<=n; i++) 42 { 43 cout << data[i] << " "; 44 } 45 int temp=n; 46 while(temp>=2) 47 { 48 minn+=he; 49 he-=data[temp]; 50 temp--; 51 } 52 */ 53 cout << minn;//输出 54 return 0; 55 }
谢谢观看~
