图的存储
前提:
在 OI 中,想要对图进行操作,就需要先学习图的存储方式。
假设有一个有图,有n个点,m条边,从点到另一点的边权为w,现要存储这个图共有几种办法?
方法一:邻接矩阵
首先,定义一个n*n的数组data,data[ i ][ j ]表示从点i到点j是否连通。
1 int data[n][n]=0;
接着输入每一条边并存入数组。
1 int x,y,z; 2 for(int i=1; i<=m; i++) 3 { 4 cin >> x >> y >> z; 5 data[x][y] = z; 6 }
ps:若为无向图,则data[ y ][ x ]再赋值。若无边权,则不用输入z,data[ x ][ y ]赋值为1即可。
这样就写好啦~ 然后是一些使用场景。
1.判断点i与点j间是否有边:
1 bool pd(int a,int b)//判断点a与点b间是否有边 2 { 3 return data[a][b]; 4 }
操作极其方便简单~
2.判断各顶点的度:
1 int r1(int a)//判断入度 2 { 3 int t=0; 4 for(int i=1; i<=n; i++) 5 { 6 if(data[i][a]) t++; 7 } 8 return t; 9 } 10 11 int r2(int a)//判断出度 12 { 13 int t=0; 14 for(int i=1; i<=n; i++) 15 { 16 if(data[a][i]) t++; 17 } 18 return t; 19 }
也不难诶~
优点:可快速判断两点间是否有边,便于计算各顶点的度;
缺点:不便于增减定点,不便于快速访问一个点的邻接点,空间复杂度高。
完整代码:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 int n,m;//顶点数与边数 6 int data[105][105];//矩阵 7 int x,y,z; 8 9 bool pd(int a,int b)//判断点a与点b间是否有边 10 { 11 return data[a][b];//若有边则返回1,否则就是0 12 } 13 14 int r1(int a)//判断入度 15 { 16 int t=0;//统计入度 17 for(int i=1; i<=n; i++) 18 { 19 if(data[i][a]) t++;//data[i][a]判断点i是否通向点a,若不为0,则有边,加1 20 } 21 return t; 22 } 23 24 int r2(int a)//判断出度 25 { 26 int t=0;//统计出度 27 for(int i=1; i<=n; i++) 28 { 29 if(data[a][i]) t++;//判断点a是否通向点i 30 } 31 return t; 32 } 33 34 int main() 35 { 36 memset(data,0,sizeof(data)); 37 //若data数组定义在main函数内,则必须赋值;本代码定义在main函数外,默认为0,此句可删 38 cin >> n >> m; 39 for(int i=1; i<=m; i++) 40 { 41 cin >> x >> y >> z; 42 data[x][y] = z; 43 //若为无向图,则data[y][x]再赋值。若无边权,则不用输入z,data[x][y]赋值为1即可 44 } 45 int a,b; 46 for(int i=1; i<=m; i++)//此处m可改,比0大就行 47 { 48 cin >> a >> b; 49 if(pd(a,b)) cout << "有" << endl; 50 else cout << "无" << endl; 51 } 52 for(int i=1; i<=n; i++)//n个顶点的度 53 { 54 cout << i << "的入度为" << r1(i) << ",出度为" << r2(i) << endl; 55 } 56 return 0; 57 }
以上结束(^-^)
方法二:边集数组
首先,定义一个结构体,以存储边的起始点和边权。
1 struct kk{ 2 int u,v,w; 3 }e[105];//依旧视m决定
输入大家都会,输入我懒得写
那赋值我也不写了~
那么接下来写出下图的边集数组:
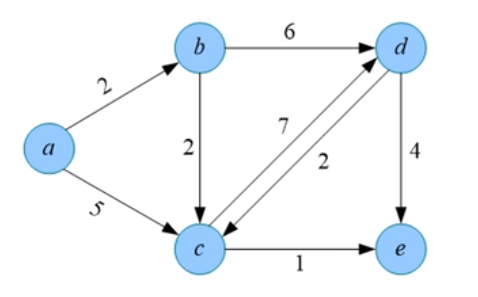
| 边 | u | v | w |
| 1 | a | b | 2 |
| 2 | a | c | 5 |
| 3 | b | d | 6 |
| 4 | b | c | 2 |
| 5 | c | d | 7 |
| 6 | c | e | 1 |
| 7 | d | c | 2 |
| 8 | d | e | 4 |
顺序输入如上表,但如果题目黑心不顺序输入怎么办呢?
排序吧~
1 struct kk{ 2 int u,v,w; 3 friend bool operator <(kk a,kk b) 4 { 5 return a.w<b.w; 6 } 7 }e[105];//依旧视m决定 8 9 bool cmp(kk a,kk b) 10 { 11 if(a.u==b.u) return a.v<b.v; 12 return a.u<b.u; 13 }
然后就差不多啦~
优点:可对边按边权、边的大小进行排序或处理(所以常用于最小生成树);
缺点:不便于判断两点间是否有边,不便于快速访问一个点的邻接点,不便于计算各顶点的度。
代码:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 int n,m;//顶点数与边数 6 struct kk{ 7 int u,v,w; 8 friend bool operator <(kk a,kk b) 9 { 10 return a.w<b.w; 11 } 12 }e[105];//依旧视m决定 13 int x,y,z; 14 15 bool cmp(kk a,kk b) 16 { 17 if(a.u==b.u) return a.v<b.v; 18 return a.u<b.u; 19 } 20 21 int main() 22 { 23 cin >> n >> m; 24 for(int i=1; i<=m; i++) 25 { 26 cin >> x >> y >> z; 27 if(x>y) swap(x,y);//无向图才有的操作~ 28 e[i].u = x; 29 e[i].v = y; 30 e[i].w = z; 31 } 32 return 0; 33 }
OK啦~
方法三:链式前向星
我写过(^—^)~
详细链接:链式前向星
方法四:邻接表(动态数组)
首先,用结构体创建一个vector数组。
1 struct kk 2 { 3 int to;//下一个点 4 int w;//边权 5 }; 6 7 vector <kk> e[105];//e[i]中i表示出发点
然后,输入我就不写啦
接着,将输入数据存入vector数组~
1 while(m--) 2 { 3 kk t; 4 cin >>temp >> t.to >> t.w;//输入出发点,终点,边权 5 e[temp].push_back(t);//将数据存入动态数组,表示在这个出发点下的所有边 6 //就相当于二维动态数组 7 }
就结束啦(^_^)
输出看看~
1 for(int i=1; i<=n; i++)//按照出发点的顺序遍历 2 { 3 for(int j=0; j<e[i].size(); j++)//遍历出发点下的所有边 4 { 5 kk t=e[i][j];//以二维数组形式输出 6 cout << "从 " << i <<" 到 " << t.to << " 的边权为 " << t.w << endl; 7 } 8 }
优点:便于增删顶点,便于快速访问一个点的邻接点,空间复杂度低(这条最重要!!!)
缺点:不便于判断两点间是否有边,不便于计算各顶点的度。
代码:
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 struct kk 6 { 7 int to;//下一个点 8 int w;//边权 9 }; 10 11 vector <kk> e[105];//e[i]中i表示出发点 12 int n,m; 13 int temp;//出发点 14 15 int main() 16 { 17 cin >> n >> m; 18 while(m--) 19 { 20 kk t; 21 cin >>temp >> t.to >> t.w;//输入出发点,终点,边权 22 e[temp].push_back(t);//将数据存入动态数组,表示在这个出发点下的所有边 23 //就相当于二维动态数组 24 } 25 for(int i=1; i<=n; i++)//按照出发点的顺序遍历 26 { 27 for(int j=0; j<e[i].size(); j++)//遍历出发点下的所有边 28 { 29 kk t=e[i][j];//以二维数组形式输出 30 cout << "从 " << i <<" 到 " << t.to << " 的边权为 " << t.w << endl; 31 } 32 } 33 return 0; 34 }
就没啦~~~~~~
谢谢观看(^ —^)



