一致性哈希的理解与实践
在维基百科中这样定义一致性哈希算法:
一致哈希 是一种特殊的哈希算法。在使用一致哈希算法后,哈希表槽位数(大小)的改变平均只需要对
K/n个关键字重新映射,其中K是关键字的数量,n是槽位数量。然而在传统的哈希表中,添加或删除一个槽位几乎需要对所有关键字进行重新映射。
好吧,初次接触,看不懂,我们从传统的哈希算法开始讲起。
1. 传统哈希算法
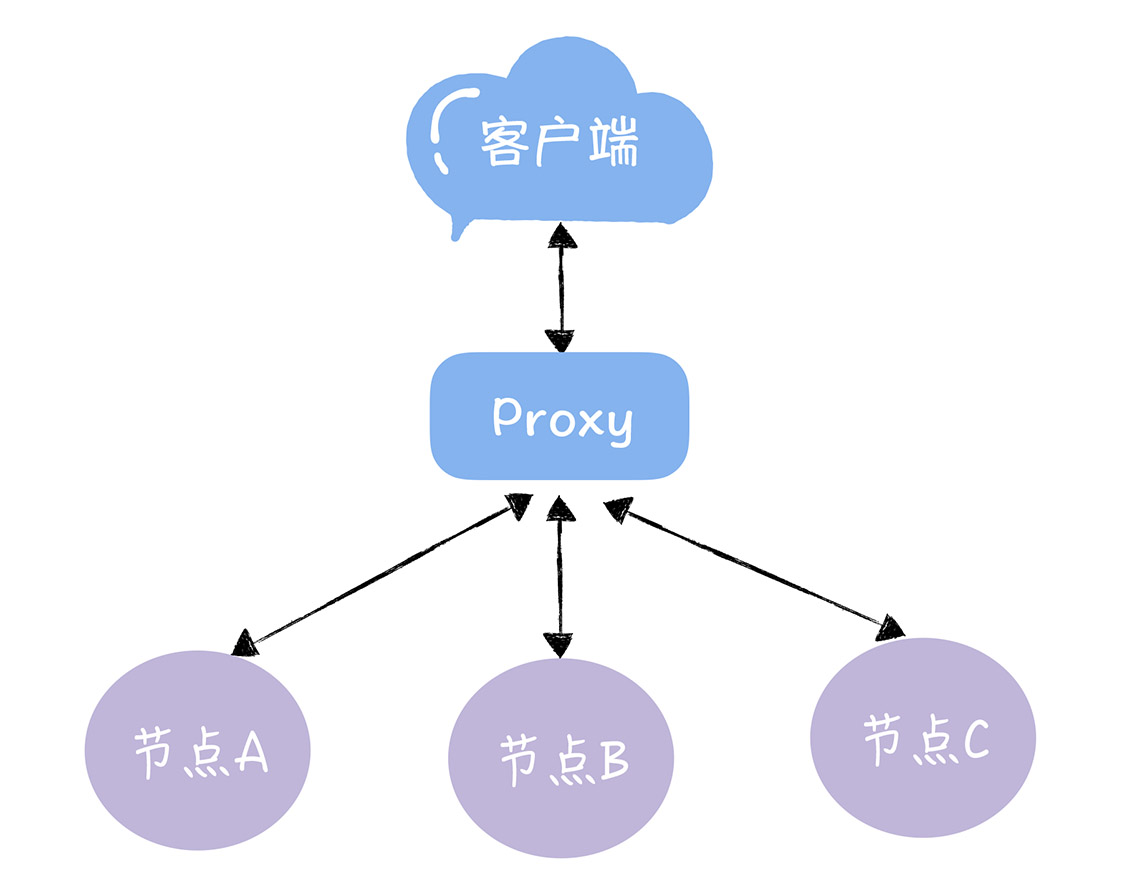
随着业务的发展,数据量的提升,我们需要增加服务器节点。对于客户端发来的请求,我们首先通过一个Proxy层,由Proxy层处理来自客户端的读写请求,接收到读写请求后,通过对 Key 做哈希找到对应的节点。如下图所示:
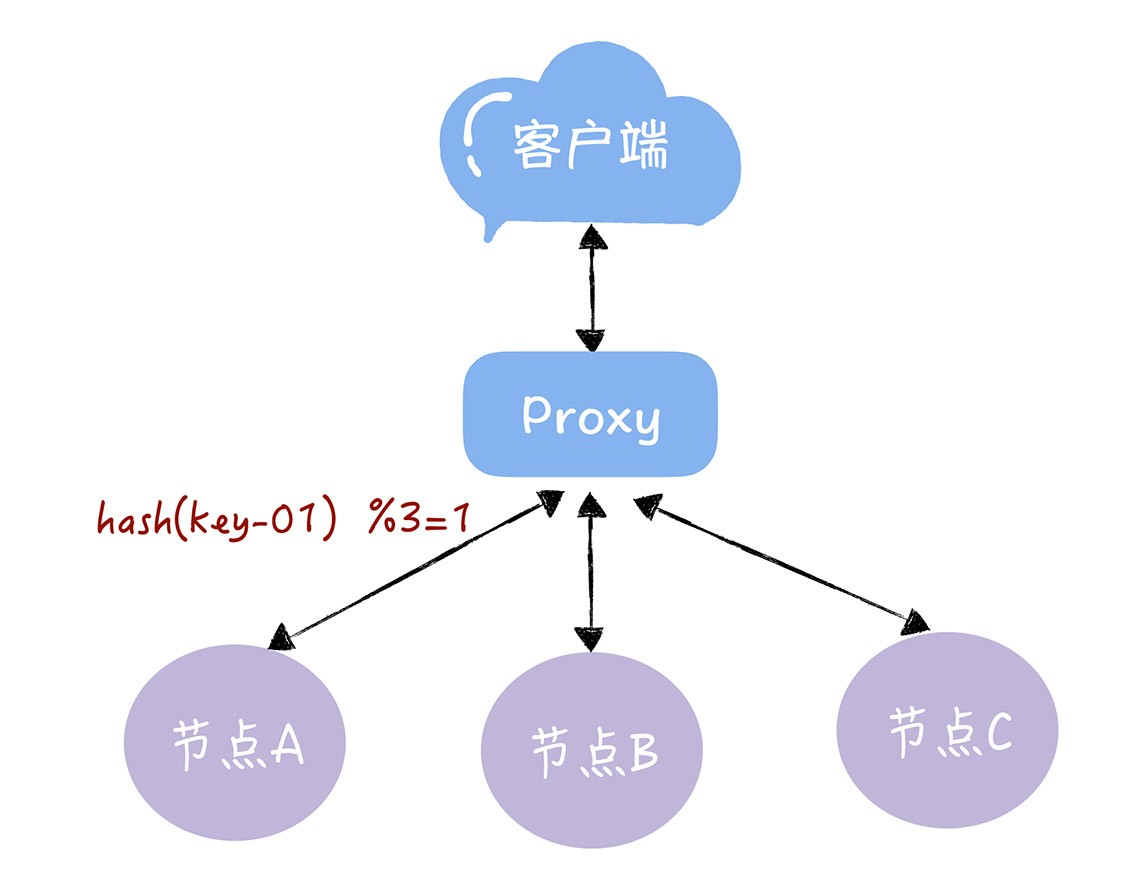
通过哈希算法,每个 key 都可以寻址到对应的服务器,假设客户端发过来的请求是 key-01,计算公式为 hash(key-01) % 3 ,经过计算寻址到了编号为 1 的服务器节点 A,如下图所示。
但如果服务器数量发生变化,基于新的服务器数量来执行哈希算法的时候,就会出现路由寻址失败的情况,Proxy 无法找到之前寻址到的那个服务器节点,这是为什么呢?想象一下,假如 3 个节点不能满足业务需要了,这时我们增加了一个节点,节点的数量从 3 变化为 4,那么之前的 hash(key-01) % 3 = 1,就变成了 hash(key-01) % 4 = X,因为取模运算发生了变化,所以这个 X 大概率不是 1,这时你再查询,就会找不到数据了,因为 key-01 对应的数据,存储在节点 A 上,而不是节点 B。同样的道理,如果我们需要下线 1 个服务器节点(也就是缩容),也会存在类似的可能查询不到数据的问题。
为了解决这一问题,我们就需要迁移数据,基于新的计算公式 hash(key-01) % 4 ,来重新对数据和节点做映射。需要注意的是,数据的迁移成本是非常高的。通过一个具体的场景进行说明:
假定有1000万条数据,原先存储在3个节点上,如果我们增加1个节点,需要迁移多少数据?
下面通过代码验证:(完整代码在这里)
// 传统的哈希映射
func hash(key int, nodes int) int {
return key % nodes
}
// migrate:需要迁移的数据量
// keys:数据量(1000万)
// nodes:旧集群的节点个数
// newNodes:新集群的节点个数
// migrateRatio:数据迁移率
migrate := 0
for i := 0; i < keys; i++ {
if hash(i, nodes) != hash(i, newNodes) {
migrate++
}
}
migrateRatio := float64(migrate) / float64(keys)
通过执行:
$ go run ./hash.go -keys 10000000 -nodes 3 -new-nodes 4
74.999980%
可以看到,我们需要迁移75%的数据。因为普通的哈希映射强依赖于集群的节点个数,当增加或减少节点个数时,映射关系就会发生动荡的变化,这在生产环境中是不可容忍的。
为了解决这一问题,就引出了一致性哈希算法 。
2. 一致哈希算法
2.1 原理:哈希环
一致哈希算法也用了取模运算,但与传统的哈希算法对节点的数量进行取模运算不同,一致哈希算法是对 2^32 - 1 进行取模运算(就相当于没取模啊...)。你可以想象下,一致哈希算法,将整个哈希值空间组织成一个虚拟的圆环,也就是哈希环。
在一致哈希中,通过执行哈希算法(为了演示方便,假设哈希算法函数为“c-hash()”),将节点映射到哈希环上 (通常选择节点的主机名、ip地址等作为参数执行 c-hash()),如下图所示:
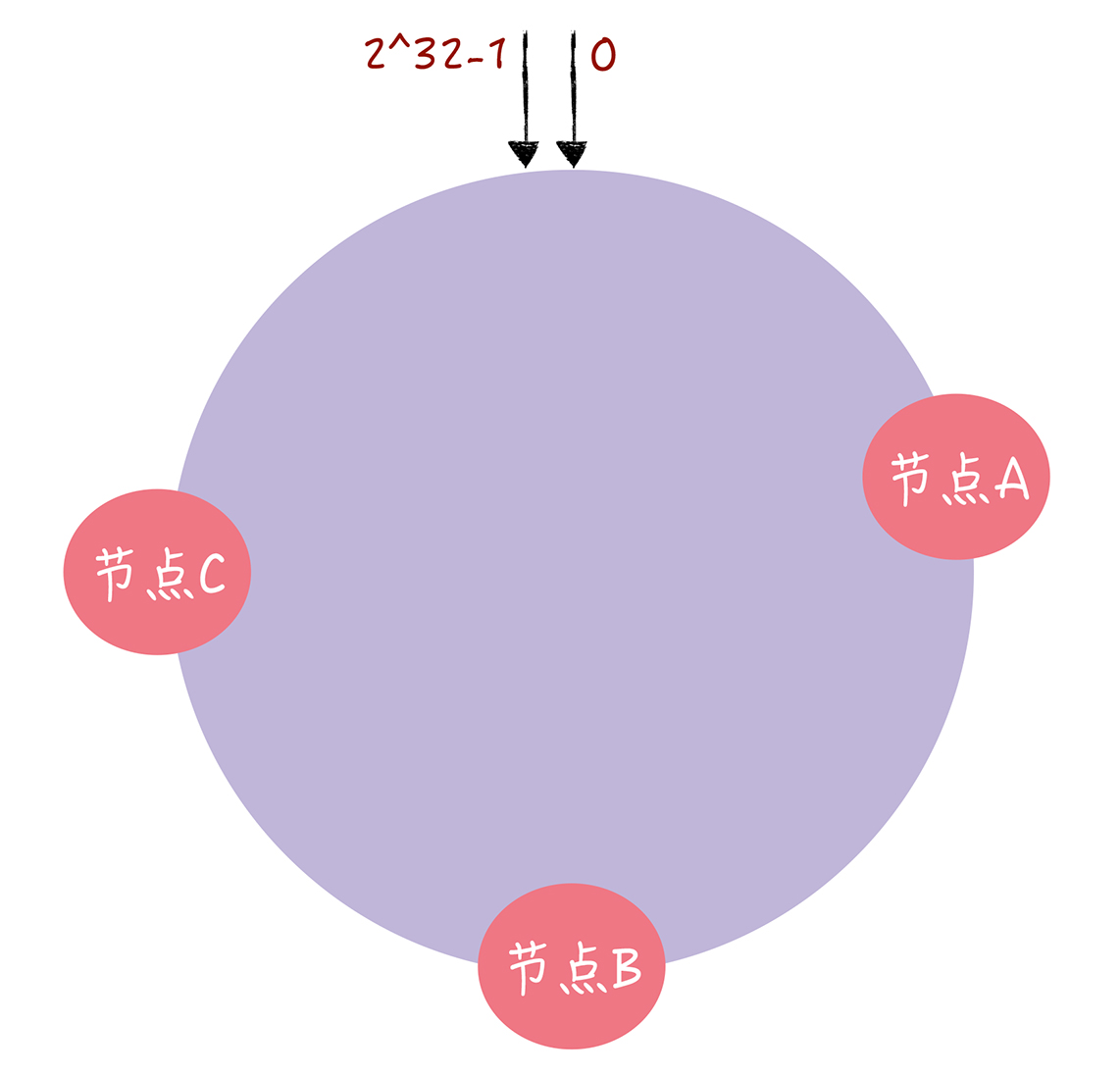
当需要对指定 key 的值进行读写的时候,你可以通过下面 2 步进行寻址:
- 首先,将 key 作为参数执行 c-hash() 计算哈希值,并确定此 key 在环上的位置;
- 然后,从这个位置沿着哈希环顺时针“行走”,遇到的第一节点就是 key 对应的节点。
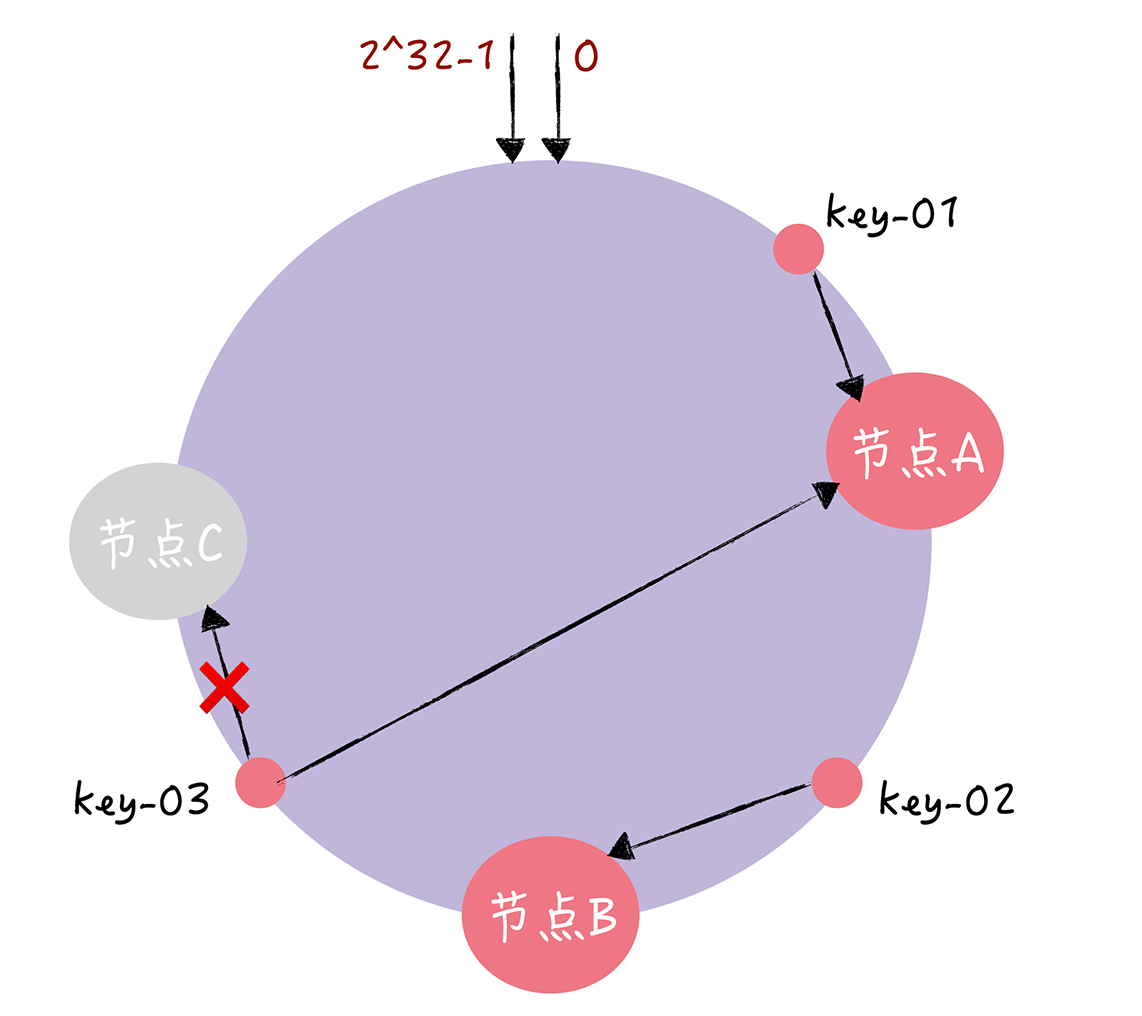
这一过程如下图所示:
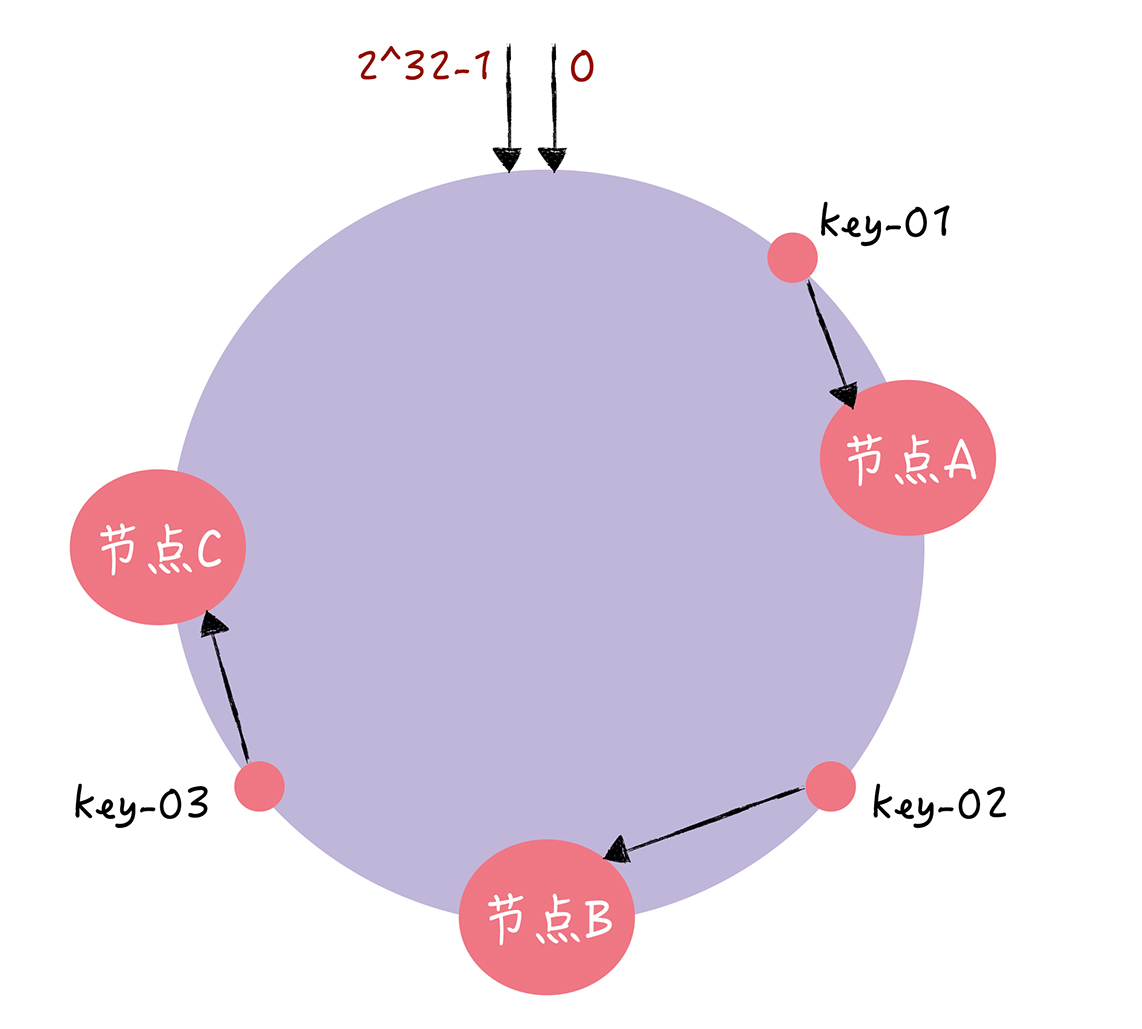
可以看到,在上图中,key-01 寻址到了节点A,key-02 寻址到了节点B,key-03 寻址到了节点C。如果节点C宕机了,那么根据寻址规则,只需要把key-03重新定位到节点A即可,而key-01,key-02不需要改变。也就是说,一致性哈希算法,在新增/减少节点时,只需要重新定位该节点附近的一小部分数据,而不需要重新定位所有的节点。这样就有效的解决了“增加/减少节点时需要大规模迁移数据”的问题。
2.2 问题:数据倾斜
当服务器节点较少时,容易造成节点位置分布不均的情况,从而造成数据倾斜。如下图所示,由于节点分布不均,使得大量的访问请求集中到节点A上,造成缓存节点负载不均衡。这就是数据倾斜问题。
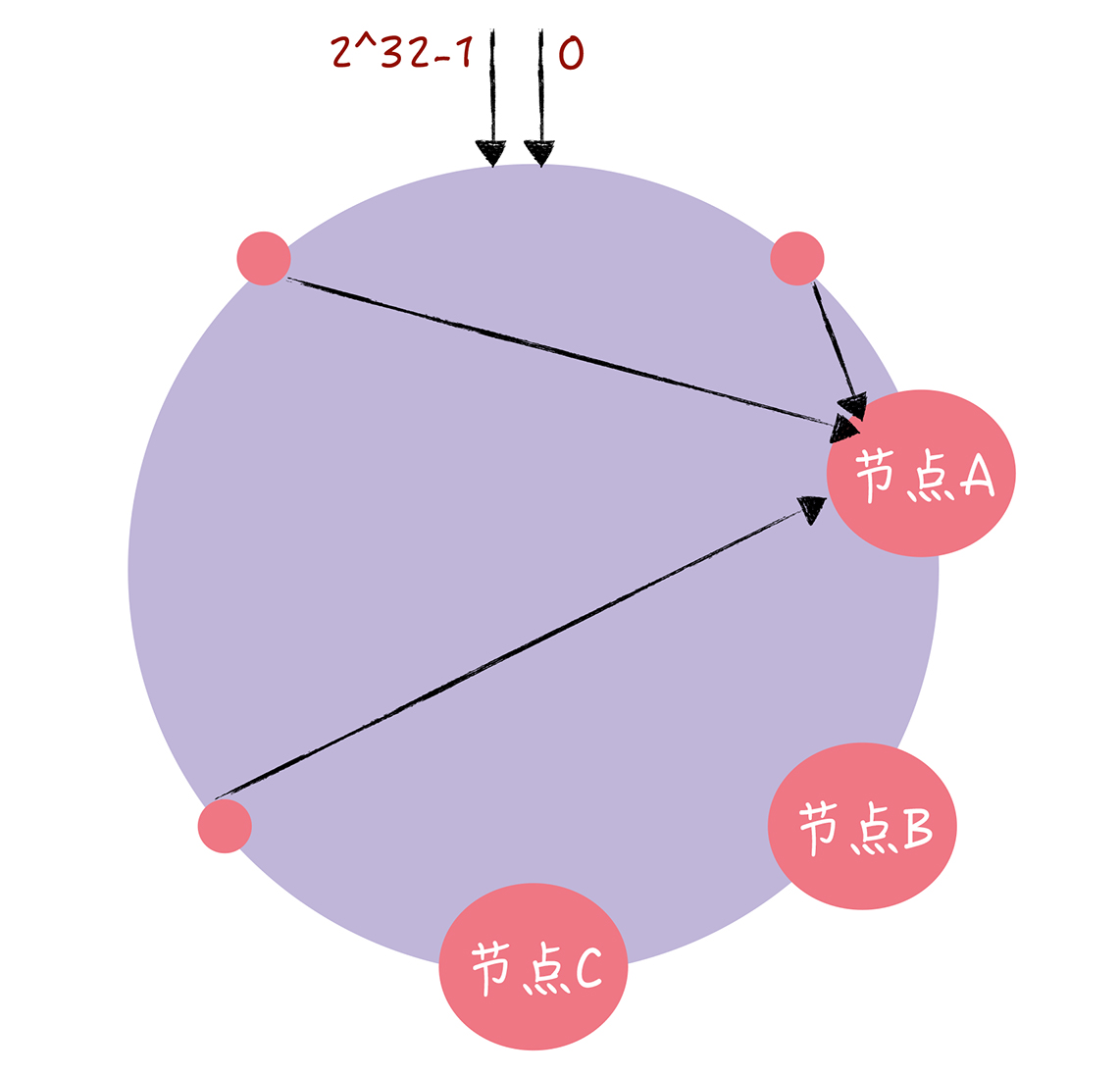
为了解决数据倾斜问题,引入了虚拟节点的概念。
2.3 改进:引入虚拟节点
所谓虚拟节点,就是对每一个服务器节点计算多个哈希值,在每个计算结果位置上,都放置一个虚拟节点,并将虚拟节点映射到实际节点。假设1个真实节点对应2个虚拟节点,那么节点A对应的虚拟节点是node-A-01,node-A-02(通常以添加编号的方式实现),其余节点类似。于是就形成了6个虚拟节点,如下图所示:
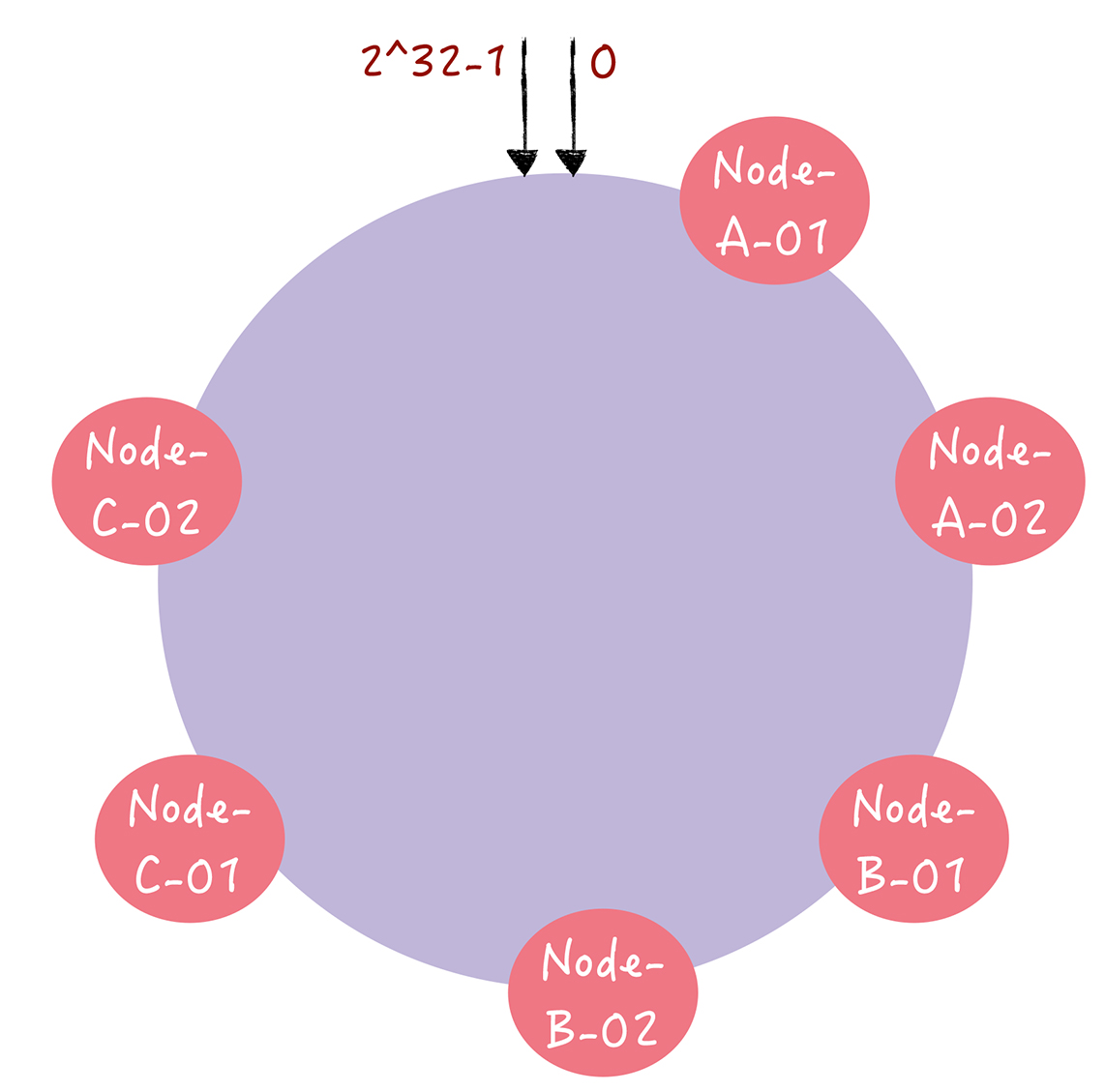
随由于节点数增多了,分布自然会变得均匀了。当寻址时,计算key的哈希值,在环上顺时针寻找应该选取的虚拟节点,比如key-01选择虚拟节点node-B-02,那么就把该请求映射到真实节点B上。
虚拟节点扩充了节点的数量,解决了节点较少的情况下数据容易倾斜的问题,而且代价非常小,只需要增加一个字典(map)维护真实节点与虚拟节点的映射关系即可。
2.4 实现
定义一致性哈希实体。
// 哈希函数签名
type Hash func(data []byte) uint32
// 一致性哈希实体
type Map struct {
hash Hash // 哈希函数
replicas int // 每个真实节点对应的虚拟节点个数
circle []int // 哈希环
hashMap map[int]string // 存储虚拟节点与真实节点的映射
}
// 创建实例
func New(replicas int, hashFunc Hash) *Map {
m := &Map{
hash: hashFunc,
replicas: replicas,
hashMap: make(map[int]string),
}
if m.hash == nil {
m.hash = crc32.ChecksumIEEE
}
return m
}
说明:
- 定义了函数类型
Hash,采取依赖注入的方式,允许用户自定义哈希函数,默认为crc32.ChecksumIEEE算法。 Map是一致性哈希算法的主数据结构,包含 4 个成员变量:Hash 函数hash;虚拟节点倍数replicas,即每个真实节点对应replicas个虚拟节点;哈希环circle;虚拟节点与真实节点的映射表hashMap,键是虚拟节点的哈希值,值是真实节点的名称。- 构造函数
New()允许自定义虚拟节点倍数和 Hash 函数。
接下来,实现添加真实节点的Add()方法。
// 添加真实节点
func (m *Map) Add(peers ...string) {
for _, peer := range peers {
for i := 0; i < m.replicas; i++ {
// 根据节点的名称+编号计算hash值
hashVal := int(m.hash([]byte(strconv.Itoa(i) + peer)))
//log.Printf("peer:[%s-%d], hash:[%d]\n", peer, i, hashVal)
m.circle = append(m.circle, hashVal)
m.hashMap[hashVal] = peer
}
}
// 排序是为了接下来方便查询
sort.Ints(m.circle)
//log.Printf("circle:\n %v\n",m.circle)
}
说明:
Add()方法允许传入0个或多个真实节点的名称。- 对每个真实节点
peer,对应创建replicas个虚拟节点,我们令虚拟节点的名称为strconv.Itoa(i) + peer,即通过添加编号的方式区分不同虚拟节点。 - 使用
m.hash()计算虚拟节点的哈希值,使用append(m.circle, hashVal)把哈希值添加到环上。 - 在
hashMap中增加虚拟节点和真实节点的映射关系。 - 最后,需要对换上的哈希值进行排序。排序是为了方便后续的查找。
最后,实现选择节点的Get()方法。
// 根据请求的key选择对应的真实节点
// 返回真实节点的名称
func (m *Map) Get(key string) string {
if len(m.circle) == 0 {
return ""
}
// 首先计算key对应的hash值
hashVal := int(m.hash([]byte(key)))
// 二分查找
index := sort.Search(len(m.circle), func(i int) bool {
return m.circle[i] >= hashVal
})
return m.hashMap[m.circle[index%len(m.circle)]]
}
说明:
Get()方法根据请求的key选择对应的真实节点,返回真实节点的名称。- 首先,对key计算对应的哈希值。
- 然后,顺时针找到第一个匹配的虚拟节点的下标
index。所谓匹配,就是在哈希环m.circle中,找到第一个哈希值大于等于key的哈希值的虚拟节点。 - 最后,通过
hashMap映射得到真实的节点。
至此,一致性哈希算法就全部完成了。
2.5 测试
我们测试一致性哈希是否能正常的增加节点和选择节点,另外,我们也测试它在增加节点时数据的迁移率如何,是否针对比传统哈希算法要好。
func TestConsistentHash(t *testing.T) {
// 创建一个一致性哈希实例,并自定义hash函数
chash := New(3, func(data []byte) uint32 {
i, _ := strconv.Atoi(string(data))
return uint32(i)
})
// 添加真实节点,为了方便说明,这里的节点名称只用数字进行表示
chash.Add("4", "6", "2")
testCases := map[string]string{
"15": "6",
"11": "2",
"23": "4",
"27": "2",
}
for k, v := range testCases {
if chash.Get(k) != v {
t.Errorf("Asking for %s, should have yielded %s", k, v)
}
}
// 新增一个节点"8",对应增加3个虚拟节点,分别为8,18,28
chash.Add("8")
// 此时如果查询的key为27,将会对应到虚拟节点28,也就是映射到真实节点8
testCases["27"] = "8"
for k, v := range testCases {
if chash.Get(k) != v {
t.Errorf("Asking for %s, should have yielded %s", k, v)
}
}
}
为了方便说明,这里简化了节点的名称(仅用数字来表示),并且自定义哈希函数。
- 一开始,有 2/4/6 三个真实节点,对应的虚拟节点的哈希值是 02/12/22、04/14/24、06/16/26。
- 那么用例 15/11/23/27 选择的虚拟节点分别是 16/12/24/02,也就是真实节点6/2/4/2。
- 新增一个节点"8",对应增加3个虚拟节点,分别为8,18,28,此时,用例 27 对应的虚拟节点从2变更为 28,即真实节点 8。
测试迁移率
var keysPtr = flag.Int("keys", 10000, "key number")
var nodesPtr = flag.Int("nodes", 3, "node number of old cluster")
var newNodesPtr = flag.Int("new-nodes", 4, "node number of new cluster")
// 测试一致性哈希的数据迁移率
func TestMigrateRatio(t *testing.T) {
flag.Parse()
var keys = *keysPtr
var nodes = *nodesPtr
var newNodes = *newNodesPtr
fmt.Printf("keys:%d, nodes:%d, newNodes:%d\n", keys, nodes, newNodes)
c := New(3, nil)
for i := 0; i < nodes; i++ {
c.Add(strconv.Itoa(i))
}
newC := New(3, nil)
for i := 0; i < newNodes; i++ {
newC.Add(strconv.Itoa(i))
}
migrate := 0
for i := 0; i < keys; i++ {
server := c.Get(strconv.Itoa(i))
newServer:= newC.Get(strconv.Itoa(i))
if server != newServer {
migrate++
}
}
migrateRatio := float64(migrate) / float64(keys)
fmt.Printf("%f%%\n", migrateRatio*100)
}
在测试迁移率的函数中,为了保证正确性,我们使用默认的hash函数来计算哈希值(前面的测试是为了方便说明所以自定义了hash函数,在这里就不能这样使用了)。通过执行如下命令,可以看到,相比于传统哈希算法,使用我们自己实现的一致哈希算法可以大大的降低数据迁移率。
$ go test -v -run=TestMigrateRatio -keys 1000000 -nodes 3 -new-nodes 4
=== RUN TestMigrateRatio
keys:1000000, nodes:3, newNodes:4
22.984500%
--- PASS: TestMigrateRatio (0.50s)
(完)
参考:



