动态规划之01背包问题
问题描述：
给定 n 件物品，物品的重量为 w[i]，物品的价值为 c[i]。现挑选物品放入背包中，假定背包能承受的最大重量为 V，问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？
针对这个问题，本人理解了多次，也了看各种题解，尝试各种办法总还觉得抽象；或者说，看了多次以后，只是把题解的状态转移方程记住了而已，并没有真正的“掌握”其背后的逻辑。直到我看了这篇文章，在此感谢作者并记录于此。
01背包问题之另一种风格的描述：
假设你是一个小偷，背着一个可装下4磅东西的背包，你可以偷窃的物品如下：
为了让偷窃的商品价值最高，你该选择哪些商品？
暴力解法
最简单的算法是：尝试各种可能的商品组合，并找出价值最高的组合。
这样显然是可行的，但是速度非常慢。在只有3件商品的情况下，你需要计算8个不同的集合；当有4件商品的时候，你需要计算16个不同的集合。每增加一件商品，需要计算的集合数都将翻倍！对于每一件商品，都有选或不选两种可能，即这种算法的运行时间是O(2ⁿ)。
动态规划
解决这样问题的答案就是使用动态规划！下面来看看动态规划的工作原理。动态规划先解决子问题，再逐步解决大问题。
对于背包问题，你先解决小背包（子背包）问题，再逐步解决原来的问题。
比较有趣的一句话是：每个动态规划都从一个网格开始。 （所以学会网格的推导至关重要，而有些题解之所以写的不好，就是因为没有给出网格的推导过程，或者说，没有说清楚为什么要”这样“设计网格。本文恰是解决了我这方面长久以来的困惑！）
背包问题的网格如下：
网格的各行表示商品，各列代表不同容量（1~4磅）的背包。所有这些列你都需要，因为它们将帮助你计算子背包的价值。
网格最初是空的。你将填充其中的每个单元格，网格填满后，就找到了问题的答案！
1. 吉他行
后面会列出计算这个网格中单元格值得公式，但现在我们先来一步一步做。首先来看第一行。
这是吉他行，意味着你将尝试将吉他装入背包。在每个单元格，都需要做一个简单的决定：偷不偷吉他？别忘了，你要找出一个价值最高的商品集合。
第一个单元格表示背包的的容量为1磅。吉他的重量也是1磅，这意味着它能装入背包！因此这个单元格包含吉他，价值为1500美元。
下面来填充网格。
与这个单元格一样，每个单元格都将包含当前可装入背包的所有商品。
来看下一个单元格。这个单元格表示背包容量为2磅，完全能够装下吉他！
这行的其他单元格也一样。别忘了，这是第一行，只有吉他可供你选择，换而言之，你假装现在还没发偷窃其他两件商品。
此时你很可能心存疑惑：原来的问题说的是4磅的背包，我们为何要考虑容量为1磅、2磅等得背包呢？前面说过，动态规划从子问题着手，逐步解决大问题。这里解决的子问题将帮助你解决大问题。
别忘了，你要做的是让背包中商品的价值最大。这行表示的是当前的最大价值。它指出，如果你有一个容量4磅的背包，可在其中装入的商品的最大价值为1500美元。
你知道这不是最终解。随着算法往下执行，你将逐步修改最大价值。
2. 音响行
我们来填充下一行——音响行。你现在处于第二行，可以偷窃的商品有吉他和音响。
我们先来看第一个单元格，它表示容量为1磅的背包。在此之前，可装入1磅背包的商品最大价值为1500美元。
该不该偷音响呢？
背包的容量为1磅，显然不能装下音响。由于容量为1磅的背包装不下音响，因此最大价值依然是1500美元。
接下来的两个单元格的情况与此相同。在这些单元格中，背包的容量分别为2磅和3磅，而以前的最大价值为1500美元。由于这些背包装不下音响，因此最大的价值保持不变。
背包容量为4磅呢？终于能够装下音响了！原来最大价值为1500美元，但如果在背包中装入音响而不是吉他，价值将为3000美元！因此还是偷音响吧。
你更新了最大价值。如果背包的容量为4磅，就能装入价值至少3000美元的商品。在这个网格中，你逐步地更新最大价值。
3. 笔记本电脑行
下面以同样的方式处理笔记本电脑。笔记本电脑重3磅，没法将其装入1磅或者2磅的背包，因此前两个单元格的最大价值仍然是1500美元。
对于容量为3磅的背包，原来的最大价值为1500美元，但现在你可以选择偷窃价值2000美元的笔记本电脑而不是吉他，这样新的最大价值将为2000美元。
对于容量为4磅的背包，情况很有趣。这是非常重要的部分。当前的最大价值为3000美元，你可不偷音响，而偷笔记本电脑，但它只值2000美元。
价值没有原来高，但是等一等，笔记本电脑的重量只有3磅，背包还有1磅的重量没用！
在1磅的容量中，可装入的商品的最大价值是多少呢？ 你之前计算过！
根据之前计算的最大价值可知，在1磅的容量中可装入吉他，价值1500美元。因此，你需要做如下的比较：
你可能始终心存疑惑：为何计算小背包可装入的商品的最大价值呢？但愿你现在明白了其中的原因！当出现部分剩余空间时，你可根据这些子问题的答案来确定余下的空间可装入哪些商品。笔记本电脑和吉他的总价值为3500美元，因此偷它们是更好的选择。
最终的网格类似于下面这样。
答案如下：将吉他和笔记本电脑装入背包时价值更高，为3500美元。
你可能认为，计算最后一个单元格的价值时，我使用了不同的公式。那是因为填充之前的单元格时，我故意避开了一些复杂的因素。其实，计算每个单元格的价值时，使用的公式都相同。这个公式如下。
你可以使用这个公式来计算每个单元格的价值，最终的网格将与前一个网格相同。现在你明白了为何要求解子问题了吧？——因为你可以合并两个子问题的解来得到更大问题的解。
4. 等等，再增加一件商品将如何变化呢？
假设你发现还有第四件商品可偷——一个iPhone！（或许你会毫不犹豫的拿走，但是请别忘了问题的本身是要拿走价值最大的商品）
此时需要重新执行前面所做的计算吗？不需要。别忘了，动态规划逐步计算最大价值。到目前为止，计算出的最大价值如下：
这意味着背包容量为4磅时，你最多可偷价值3500美元的商品。但这是以前的情况，下面再添加表示iPhone的行。
我们还是从第一个单元格开始。iPhone可装入容量为1磅的背包。之前的最大价值为1500美元，但iPhone价值2000美元，因此该偷iPhone而不是吉他。
在下一个单元格中，你可装入iPhone和吉他。
对于第三个单元格，也没有比装入iPhone和吉他更好的选择了。
对于最后一个单元格，情况比较有趣。当前的最大价值为3500美元，但你可以偷iPhone，这将余下3磅的容量。
3磅容量的最大价值为2000美元！再加上iPhone价值2000美元，总价值为4000美元。新的最大价值诞生了！
最终的网格如下：
相信看到这里，并且亲手推导过网格，应该对动态规划的状态转移方程背后的逻辑有了更深的理解。现在，再回头看01背包问题的经典描述，并实现代码。
问题描述：
给定 3 件物品，物品的重量为 weight[]={1,3,1}，对应的价值为 value[]={15,30,20}。现挑选物品放入背包中，假定背包能承受的最大重量 W 为 4，问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？
令 dp[i][w] 表示前 i 件物品放入容量为 w 的背包中可获得的最大价值。为了方便处理，我们约定下标从 1 开始。初始时，网格如下：
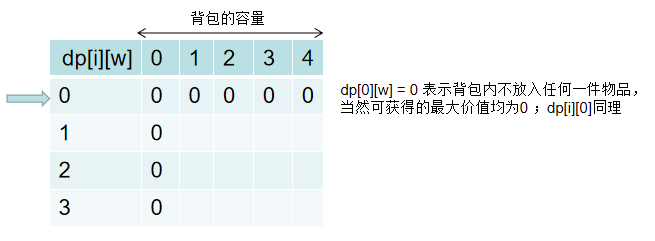
根据之前已经引出的状态转移方程，我们再来理解一遍，对于编号为 i 的物品：
-
如果选择它，那么，当前背包的最大价值等于” i 号物品的价值“ 加上 ”减去 i 号物品占用的空间后剩余的背包空间所能存放的最大价值“，即dp[i][k] = value[i] + dp[i-1][k-weight[i]]；
-
如果不选择它，那么，当前背包的价值就等于前 i-1 个物品存放在背包中的最大价值，即 dp[i][k] = dp[i-1][k]
dp[i][k] 的结果取两者的较大值，即：
dp[i][k] = max(value[i] + dp[i-1][k-weight[i]], dp[i-1][k])
动态规划
代码实现如下：
public class BeiBao01 {
public int maxValue(int[] weight, int[] value, int W) {
//这里假定传入的weight和values数组长度总是一致的
int n = weight.length;
if (n == 0) return 0;
int[][] dp = new int[n + 1][W + 1];
for (int i = 1; i <= n; i++) {
for (int k = 1; k <= W; k++) {
// 存放 i 号物品（前提是放得下这件物品）
int valueWith_i = (k-weight[i-1] >= 0) ? (value[i-1]+dp[i-1][k-weight[i-1]]) : 0;
// 不存放 i 号物品
int valueWithout_i = dp[i - 1][k];
dp[i][k] = Math.max(valueWith_i, valueWithout_i);
}
}
return dp[n][W];
}
public static void main(String[] args) {
BeiBao01 obj = new BeiBao01();
int[] w = {1, 4, 3};
int[] v = {15, 30, 20};
int W = 4;
System.out.println(obj.maxValue(w, v, W));
}
}
下面实现的版本稍有不同：
public int maxValue(int[] weight, int[] value, int W) {
int n = weight.length;
if (n == 0) return 0;
int[][] dp = new int[n][W + 1];
// 先初始化第 0 行，也就是尝试把 0 号物品放入容量为 k 的背包中
for (int k = 1; k <= W; k++) {
if (k >= weight[0]) dp[0][k] = value[0];
else dp[0][k] = 0; // 这一步其实没必要写，因为dp[][]数组默认就是0
}
for (int i = 1; i < n; i++) {
for (int k = 1; k <= W; k++) {
// 存放 i 号物品（前提是放得下这件物品）
int valueWith_i = (k-weight[i] >= 0) ? (value[i] + dp[i-1][k-weight[i]]) : 0;
// 不存放 i 号物品
int valueWithout_i = dp[i-1][k];
dp[i][k] = Math.max(valueWith_i, valueWithout_i);
}
}
return dp[n-1][W];
}
对应的初始化网格如下：
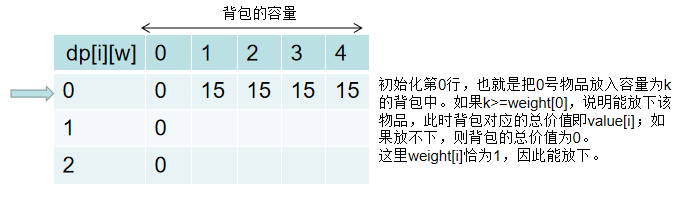
（个人更喜欢第二种实现方式，感觉理解起来更友好）
时间复杂度：O(nW)；空间复杂度：O(nW)
动态规划+压缩空间
观察上面的代码，会发现，当更新dp[i][..]时，只与dp[i-1][..]有关，也就是说，我们没有必要使用O(n*W)的空间，而是只使用O(W)的空间即可。下面先给出代码，再结合图例进行说明。
public int maxValue(int[] weight, int[] value, int W) {
int n = weight.length;
if (n == 0) return 0;
// 辅助空间只需要O(W)即可
int[] dp = new int[W + 1];
for (int i = 0; i < n; i++) {
// 注意这里必须从后向前！！！
for (int k = W; k >= 1; k--) {
int valueWith_i = (k - weight[i] >= 0) ? (dp[k - weight[i]] + value[i]) : 0;
int valueWithout_i = dp[k];
dp[k] = Math.max(valueWith_i, valueWithout_i);
}
}
return dp[W];
}
这里的状态转移方程变成了：dp[k](新值) = max(value[i]+dp[k-weight[i]](旧值), dp[k](旧值))
为什么说这里必须反向遍历来更新dp[]数组的值呢？原因是索引较小的元素可能会被覆盖。我们来看例子，假设我们已经遍历完了第 i=1 个元素（即weight=3, value=30），如下图所示：
现在要更新第 i=2 个元素（即weight=1, value=20），由于我们只申请了一维空间的数组，因此对dp[]数组的修改会覆盖上一轮dp[]数组的值，这里用浅色代表上一轮的值，深色代表当前这一轮的值。
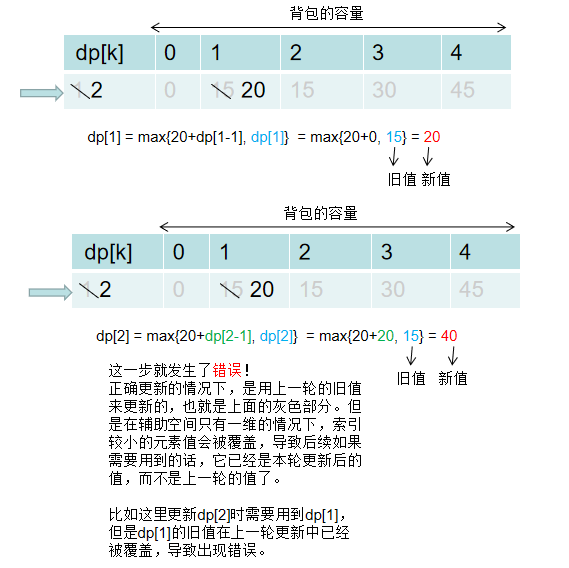
鉴于上面出现的问题，因此必须采用反向遍历来回避这个问题。仍然假设第 i=1 个元素已经更新完毕，现在更新第 i=2 个元素。示意图如下：
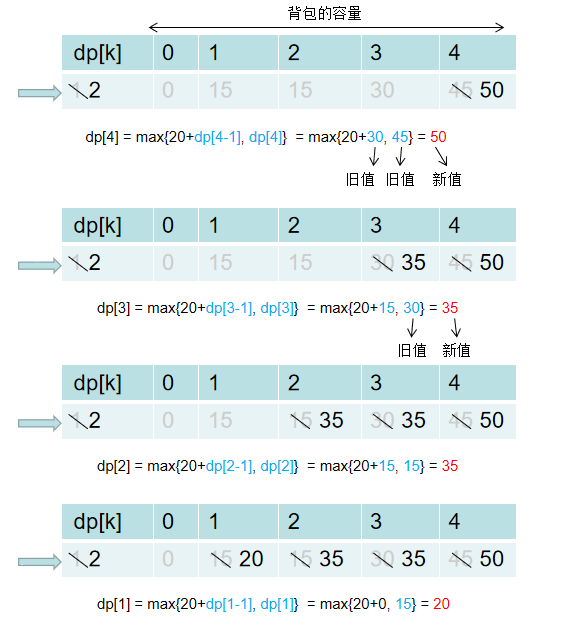
可以看到，反向遍历就可以避免这个问题了！
事实上，我们还可以进一步简化上面的代码，如下：
public int maxValue(int[] weight, int[] value, int W) {
int n = weight.length;
if (n == 0) return 0;
int[] dp = new int[W + 1];
for (int i = 0; i < n; i++) {
//只要确保 k>=weight[i] 即可，而不是 k>=1，从而减少遍历的次数
for (int k = W; k >= weight[i]; k--) {
dp[k] = Math.max(dp[k - weight[i]] + value[i], dp[k]);
}
}
return dp[W];
}
为什么可以这样简化呢？我们重新看一下这段代码：
for (int k = W; k >= 1; k--) {
int valueWith_i = (k - weight[i] >= 0) ? (dp[k - weight[i]] + value[i]) : 0;
int valueWithout_i = dp[k];
dp[k] = Math.max(valueWith_i, valueWithout_i);
}
如果k>=weight[i] 不成立，则valueWith_i 的值为0，那么显然有：
dp[k] = Math.max(valueWith_i, valueWithout_i) = max(0, dp[k]) = dp[k]
也就是dp[k]没有更新过，它的值还是上一轮的值，因此就没必要执行了，可以提前退出循环！
至此，01背包问题就全部讲完了。（图画的好累~）
更好的阅读体验请前往：这里
