倒排索引

索引是计算机科学领域中非常常用的数据结构，比如数据库中的索引。索引的目的就是为了加快查找速度，具体到搜索引擎中，索引更是扮演了非常重要的角色，面对海量的网页内容，如何快速找到包含用户查询关键词的所有网页呢？——这其中就用到了倒排索引！

 

什么是倒排索引？如何建立倒排索引表？倒排索引表有什么作用？......

 

在回答这些问题之前，先要了解一下“单词-文档矩阵”的概念。

 

所谓“单词-文档矩阵”，就是一种表达单词和文档之间所具有的包含关系的概念模型。如下：

 

纵向看：表示某文档包含哪些单词（如文档1包含单词1和单词4）

横向看：表示某单词出现在哪些文档中（如单词1出现在文档1和文档4中）

 

而搜索引擎的索引就是实现“单词-文档矩阵”的具体数据结构，如有倒排索引，后缀树等。其中，倒排索引是最佳的实现方式。

 

概括的说，倒排索引就是一种实现“单词-文档矩阵”的数据结构，它常常用作搜索引擎的索引结构。

 

在继续讲解之前，我们需要明白几个基本概念。

• 文档：一般搜索引擎的处理对象是网页。而文档的概念则要更加宽泛一些，凡是以文本形式存在的存储对象，比如.doc，.txt，.html等格式的文件都是文档。在这里，可以简单的把文档理解成网页。
• 文档集合：由若干篇文档构成的集合就称为文档集合。对于搜索引擎而言，文档集合就是从互联网上爬下来的所有网页的集合，这个数据是巨大的，为了存储这些海量的数据从而有了分布式存储。在我的这个小项目中，我就只爬取了几百篇博客作为我的文档集合。
• 文档编号：在搜索引擎内部，每篇文档会有唯一的编号作为标记，方便数据处理。记文档编号为docID。
• 倒排列表：倒排列表记录了出现过某个单词的文档列表，以及单词在文档中的一些信息（比如权重，位置等），每条记录称为倒排项。通过倒排列表，即可获得包含某一单词的所有的文档。
• 单词词典：搜索引擎的索引单位通常是单词，单词词典是由文档集合中出现过的所有单词构成的。

搜索引擎的网页数以亿计，设想，查找一个关键词，如果从头到尾遍历所有文章（即正向索引），这是极其耗费时间的。而利用倒排索引就能很快找到包含该关键词的文档，这就是倒排索引的厉害之处了。即建立倒排索引的作用是为了提高搜索引擎的查询效率，可以这么说，倒排索引是搜索引擎最关键的一个数据结构！

 

下面是倒排索引的一个简单实例。

 

假设文档集合包含5个文档，如下图所示，我们的任务就是对这个文档集合建立倒排索引。

 

 

对于英文，各个单词之间是分割开的，很好处理；对于中文，则需要分词算法先把一句连续的话切分成一个个单词，比如，"南京市长江大桥"到底是切分成{"南京", "市长", "江大桥"}还是{"南京市", 长江大桥"}就是分词算法做的事情。但这不是讨论的重点，我们假设，能很好的对中文文档进行分词。对于不同的单词，我们为其赋予唯一的单词编号，同时记录该单词在哪些文档中出现过。基于此，我们可以得到最简单的倒排索引，如下图所示。比如，"跳槽"这一个单词的编号是4，它在文档1、4中出现过，因此该单词对应的倒排列表就是{1, 4}。

 

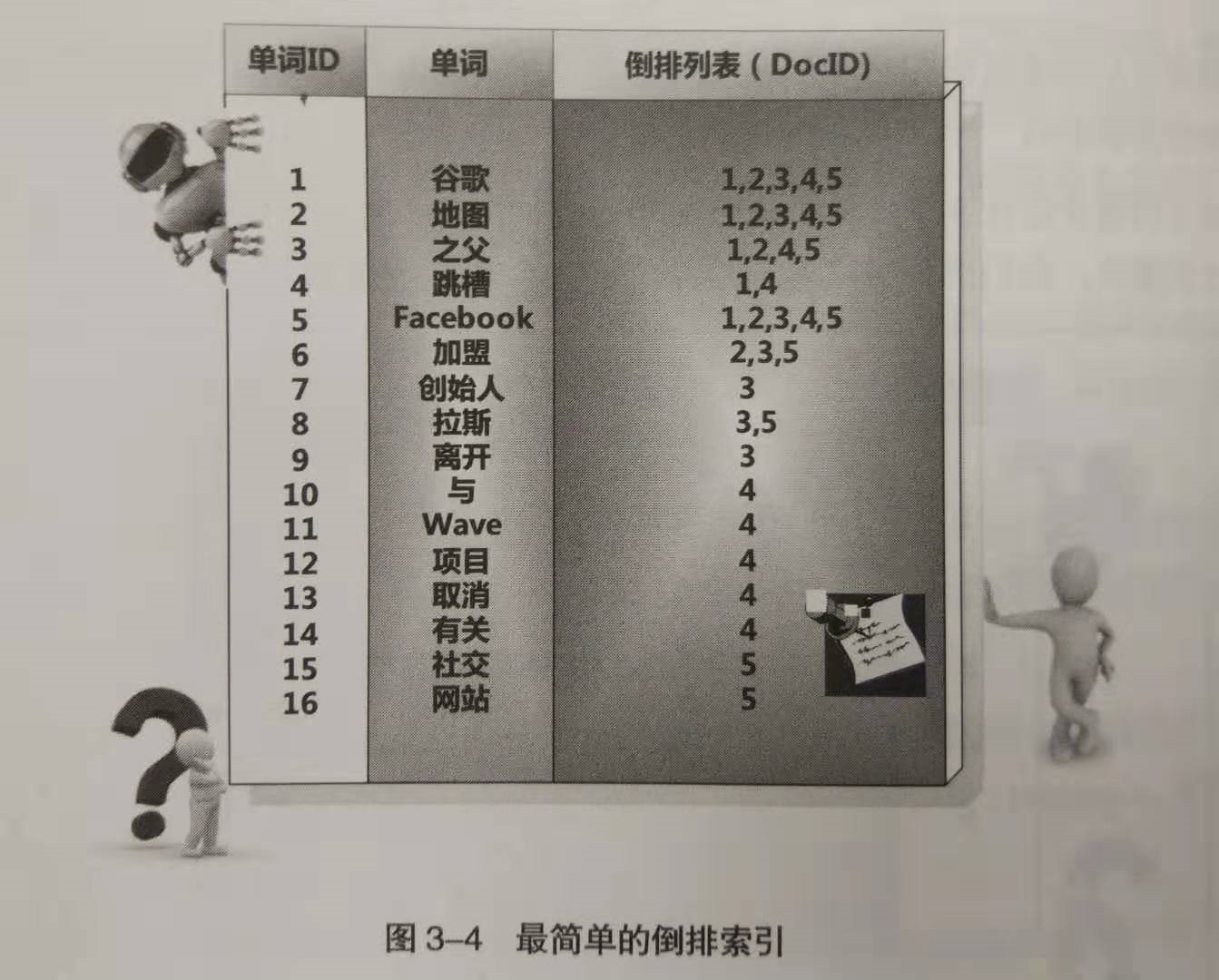
下面的倒排索引则稍微复杂了一些，不仅记录了单词在哪篇文档中出现过，还记录了单词在该文档中出现的频率（Term Frequency, TF），之所以记录这个信息，是因为词频信息在搜索结果排序时，计算查询和文档相似度是一个很重要的计算因子。比如，"跳槽"一词的倒排列表为{(1;1), (4;1)}，说明该单词在1号文档中出现过1次，在4号文档中出现过1次。

 

 下面的倒排索引则增加了文档频率（Document Frequency，DF）和单词在文中的位置信息（<pos>），还是以"跳槽"为例，其文档频率为2，表示在整个文档集合中，共有2个文档包含"跳槽"这个单词；倒排索引项(1; 1; <4>)表示该单词在1号文档中出现过1次，并且出现的位置是4，即文档中的第4个单词是"跳槽"。

注意厘清文档频率（DF）和单词频率（TF）的概念，这两个概念非常重要，在搜索结果排序计算中都是非常重要的因子。而单词在文档中的位置信息则不是必须的。

 

 

图3-6所示的倒排索引已经是一个非常完备的索引系统了，有了这个索引系统，搜索引擎就可以很方便的响应用户的查询。比如用户输入查询词"Facebook"，搜索系统查找倒排索引，从中可以读出包含这个单词的文档，这些文档就是提供给用户的搜索结果，而利用单词频率信息（TF）、文档频率信息（DF）即可对这些候选搜索结果进行排序，计算文档与查询的相似性，按照相似性得分由高到低排序输出。

 

---

在自己写的项目中应用如下：

构建倒排索引表的数据结构是
unordered_map<string, vector<pair<int, double>>> invertIndexTable; 
 
即
单词1   {docID1,weight1}, {docID2,weight2}, {docID3,weight3}...
单词2   {docID1,weight1}, {docID2,weight2}, {docID3,weight3}...
...
...
 
项目部分源码
void PagelibProcesser::createInvertIndexTable()
{
    for(auto iter = pagelib_.begin(); iter != pagelib_.end(); ++iter){ //pagelib_的结构是vector<WebPage> 
        auto docWordMap = (*iter).getDocWordMap();//词典，[单词，词频]
        for(auto it = docWordMap.begin(); it != docWordMap.end(); ++it){
            //倒排索引的结构unordered_map<string, vector<pair<int, double>>> invertIndexTable_
            invertIndexTable_[it->first].push_back({iter->getDocID(),it->second});//<单词,<docID,词频>>
        }
    }
 
    size_t totalPageNum = pagelib_.size();//网页库中网页的总数
    map<int,double> pageWeight;//每个网页的权重和
    for(auto iter = invertIndexTable_.begin(); iter != invertIndexTable_.end(); ++iter){
        size_t df = iter->second.size();//文档频率,表示单词在多少篇文档中出现过   
        double idf = log(static_cast<double>(totalPageNum)/(df+1));//逆文档频率
        for(auto & elem : iter->second){
            double weight = elem.second * idf;
            elem.second = weight;
            pageWeight[elem.first] += pow(weight,2);
        }
    }
 
    //归一化处理
    for(auto iter = invertIndexTable_.begin(); iter != invertIndexTable_.end(); ++iter){
        for(auto & elem : iter->second){
            elem.second = elem.second / sqrt(pageWeight[elem.first]);
        }
    }
}

建倒排索引时最难的是每个词语的权重值的计算，它涉及到如下几个概念：

TF:  Term Frequency, 单词在某一篇文档中出现的次数；

DF:  Document Frequency, 在文档集合中，包含该词语的文档数量；

IDF: Inverse Document Frequency, 逆文档频率，表示某一单词对于该篇文章的重要性的一个系数，其计算公式为：

IDF = log2(N/(DF+1))，其中N表示文档的总数或网页库的文档数

最后，词语的权重w则为：w = TF * IDF

 

可以看到权重系数与一个词在文档中的出现次数成正比，与该词在整个网页库中的出现次数成反比。

 

而一篇文档包含多个词语w1,w2,...,wn，还需要对这些词语的权重系数进行归一化处理，其计算公式如下：

w' = w /sqrt(w1^2 + w2^2 +...+ wn^2)

w' 才是需要保存下来的，即倒排索引的数据结构中InvertIndexTable的double类型所代表的值。此权重系数的算法称为TF-IDF算法。

做个记录，方便回顾。