最长下降子序列

最长下降子序列

一些预备知识

结构体

vs2019定义在xstddef而不是funtional

// STRUCT TEMPLATE greater
template <class _Ty = void>
struct greater {
    _CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef _Ty _FIRST_ARGUMENT_TYPE_NAME;
    _CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef _Ty _SECOND_ARGUMENT_TYPE_NAME;
    _CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef bool _RESULT_TYPE_NAME;

    constexpr bool operator()(const _Ty& _Left, const _Ty& _Right) const {
        return _Left > _Right;  //greater<_Ty>()表示内置类型从大到小排列
    }
};

类似的，还有less，greater_equal，less_equal等结构体。

二分查找

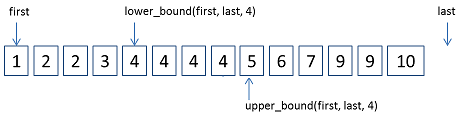
lower_boubd()函数返回的是第一个大于等于Val的地址

upper_bound()函数返回的是第一个大于Val的地址

注意区间[first,last)是左闭右开的

进入正题

主要思路就是：贪心+二分查找，复杂度是O(Nlog₂N)

最长下降子序列

开辟一个与原序列同样大小的辅助数组，遍历一遍原序列，对于从第二个元素起的每个元素：

1）当前元素若是小于辅助数组最后一个元素，那么加入到辅助数组之后

2）当前元素若是大于等于辅助数组最后一个元素，那么在辅助数组内找到第一个小于当前元素的位置，替换成当前元素

#include <iostream>
#include <algorithm>
using namespace std;
constexpr int N = 10001;
int arr[N], seq[N];
int main() {
	int arrLen, seqLen = 1;
	cin >> arrLen;
	for (int i = 0; i < arrLen; ++i)
		cin >> arr[i];

	seq[0] = arr[0];
	for (int i = 1; i < arrLen; ++i)
	{
		if (seq[seqLen - 1] > arr[i])
			seq[++seqLen - 1] = arr[i];
		else
		{
			int index = upper_bound(seq, seq + seqLen, arr[i],greater<int>()) - seq;
			seq[index] = arr[i];
		}
	}
	cout << seqLen << endl;
}

说明：upper_bound()和lower_bound()默认支持升序，得用greater<int>()自定义比较

一个测试例子：

最长升序子序列

	for (int i = 1; i < arrLen; ++i)
	{
		if (seq[seqLen - 1] < arr[i])
			seq[++seqLen - 1] = arr[i];
		else
		{
			int index = upper_bound(seq, seq + seqLen, arr[i]) - seq;
			seq[index] = arr[i];
		}
	}
	cout << seqLen << endl;

最长非升子序列，最长非降子序列也是同理。

问题延展

问题描述详见杭电的最少拦截系统，以下浅谈贪心+二分查找，复杂度在O(Nlog₂N)的做法。

假定在每一发导弹到来时，都能被最合适的来拦截系统拦下。考虑两种情形：

1）若当前没有系统可以拦截，那么新建立一个系统

2）若有系统可以拦截，那么选取大于等于导弹高度的第一个高度，用当前高度替代之(体现了前文所提“最合适”）

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100000;
int arr[N], low[N];
int main() {
	int arrLen, lowLen;

	while(cin >> arrLen) {
		for (int i = 0; i < arrLen; ++i)
			cin >> arr[i];

		low[0] = arr[0];
		lowLen = 1;

		for (int i = 1; i < arrLen; ++i)
		{
			if (low[lowLen - 1] < arr[i])  //当前无系统可拦截
				low[++lowLen - 1] = arr[i];
			else
			{
				int index = lower_bound(low, low + lowLen, arr[i]) - low;
				low[index] = arr[i];
			}
		}
		cout << lowLen << endl;
	}
}

说明

因为low维护的是一个升序数组，所以当前系统的最大拦截高度就是low最后一个元素。