图的拓扑排序（python）

what?

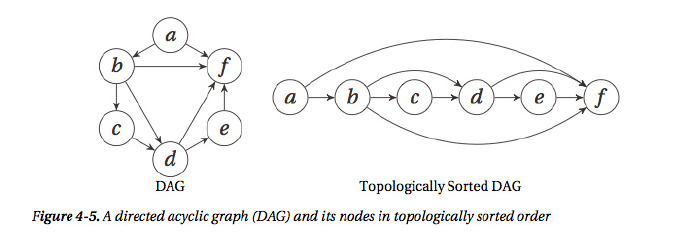
拓扑排序是指在有向图中的顶点序列，且序列满足若存在从a到b的路径，那么b排在a之后的性质。

拓扑常用来检测图中是否存在环。

how?

入度：设有向图中有一结点v，其入度即为当前所有从其他结点出发，终点为v的的边的数目。也就是所有指向v的有向边的数目。

出度：设有向图中有一结点v，其出度即为当前所有起点为v，指向其他结点的边的数目。也就是所有由v发出的边的数目。

基本思路

输出入度为零的顶点，然后删除所有以它为起始顶点的边，循环直至所有节点都被处理。

def topologicalSort(graph):
    in_degree = dict((u,0) for u in graph)   #初始化所有顶点入度为0
    vertex_num = len(in_degree)
    for u in graph:  #计算每个顶点的入度
        for v in graph[u]:
            in_degree[v] += 1
    q = [u for u in in_degree if in_degree[u] == 0]   # 筛选入度为0的顶点
    Seq = []  #拓扑序列,空列表
    while q:
        u = q.pop()  #弹出入度为0的顶点
        Seq.append(u)
        for v in graph[u]:
            in_degree[v] -= 1  #以弹出节点为起始节点的边入度-1
            if in_degree[v] == 0:
                q.append(v)  #再次筛选入度为0的顶点
    if len(Seq) == vertex_num:  #如果循环结束后存在非0入度的顶点说明图中有环，不存在拓扑排序
        return Seq
    else:
        print("There is at least one circle in the graph.")
G = {
    'a':'bf',
    'b':'cdf',
    'c':'e',
    'd':'ef',
    'e':'f',
    'f':''
}
print(topologicalSort(G))

运行结果

时间复杂度： O(n + e)，其中n为图中的结点数目，e为图中的边的数目

空间复杂度：O(n)