动态规划

动态规划

能够动态规划的问题具有以下特点：

1. 可分解成规模更小的子问题
2. 子问题的结果可复用

关键是要理解状态转移方程的含义就好啦！

数字三角形

问题描述

在数字三角形寻找从顶到底的路径，使得路径经过的数字之和最大。规定每一步只能往左下或右下走，求出最大路径和。

递归解法

#include<iostream>
#include<algorithm>
using namespace std;

constexpr int N = 100;
int numTriangle[N][N];
int n;  //数字三角形高度

int maxPath( int i, int j) {
	if (i == n)  //到达底层
		return numTriangle[i][j];
	return max(maxPath(i + 1, j) , maxPath(i + 1, j + 1)) + numTriangle[i][j];
}

int main()
{
	cin >> n;
	for (int i = 0; i < n; ++i)
		for (int j = 0; j <= i; ++j)
			cin >> numTriangle[i][j];
	cout << maxPath(0, 0);
}

存在问题

自顶向下，大量重复的计算，越靠近底层重复次数越多。

dp解法

#include<iostream>
#include<algorithm>
using namespace std;

constexpr int N = 100;
int numTriangle[N][N];
int dp[N][N];
int n;  //数字三角形高度

int main()
{
	cin >> n;
	for (int i = 0; i < n; ++i)
		for (int j = 0; j <= i; ++j)
			cin >> numTriangle[i][j];

	for (int j = 0; j < n; ++j)
		dp[n - 1][j] = numTriangle[n - 1][j];  //初始化最底层作为dp起点

	for (int i = n - 2; i >= 0; --i)
		for (int j = 0; j <= i; ++j)
			dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + numTriangle[i][j];
	cout << dp[0][0] << endl;
    
    //int x = 0, y = 0;
	//do {  //以下输出最大路径
	//	cout << numTriangle[x][y]<< ' ';
	//	if (dp[x + 1][y] > dp[x + 1][y + 1]) {
	//		++x;
	//	}
	//	else {
	//		++x;
	//		++y;
	//	}
	//} while (x < n);
}

分析

开辟另外一个二维数组，自底向上记录最大路径。其实若不要求输出具体路径，可以将dp覆盖在原数字三角形数组中以求节约空间。覆盖方式可以是每次循环都覆盖在最后一行。

0-1背包

问题描述

选择物品的组合，以期在有限的空间里装下最大价值。

Example

假定背包最大容量是10，且每种物品的重量，价值如下

weight	2	2	6	5	4
value	6	3	5	4	6

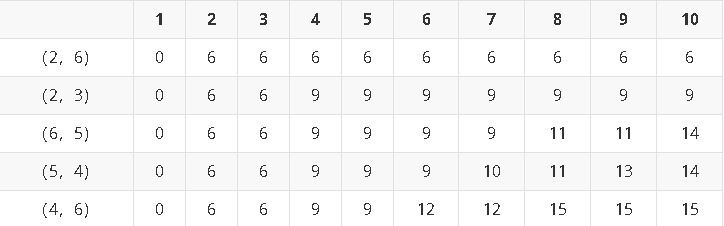
填表过程

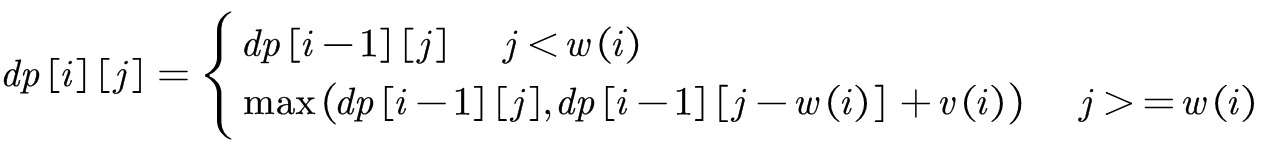
填表的过程是自上而下，从左到右，每一步都是当前情况下的最优解。

import numpy as np
import operator
capacity,kind = input().strip().split()
capacity = int(capacity)  #总容量
kind = int(kind)  #总种类

weight = np.zeros(kind + 1,dtype = int)
value = np.zeros(kind + 1,dtype = int)

for i in range(1,kind+1):
    weight[i],value[i] = input().strip().split()  

dp = np.zeros((kind+1,capacity+1),dtype = int)  #记录动态规划过程的表格

for i in range(1,kind+1):
    for j in range(1,capacity+1):
        if(operator.lt(j,weight[i])):  #在当前容量下，若装不下，不装
            dp[i][j] = dp[i-1][j]
        else:
            dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])  #在当前容量下，若装得下，取装与不装的最大值

print(dp[kind][capacity])

分析

可是使用一维数组来作空间优化，带来的缺点是无法回溯具体是选择那几样物品。通过观察状态转移方程可以得知，dp[i][j]只与dp[i-1][j]，dp[i-1][j-w(i)]有关，能够下一行覆盖上一行。但是在内循环中，若是依旧从左往右，计算dp[i-1][j-w(i)]时这个值已经被更新导致失效，所以内循环需要逆序扫描。

#include <iostream>
#include<algorithm>
using std::cin;
using std::cout;
using std::endl;
int dp[100];
int value[100], weight[100];
int main()
{
	int m, n;
	cin >> m >> n;
	for (int i = 0; i < n; ++i)
		cin >> weight[i] >> value[i];

	for (int i = 0; i < n; ++i)
		for (int j = m - 1; j >= weight[i]; --j)
				dp[j] = std::max(dp[j], dp[j - weight[i]] + value[i]);
	cout << dp[m - 1] << endl;
}

最长公共子序列

问题描述

Longest common Subsequence，从给定的两个序列中取得尽可能多的字符，要求按原序列的先后次序得到。（不要求连续）

状态转移方程

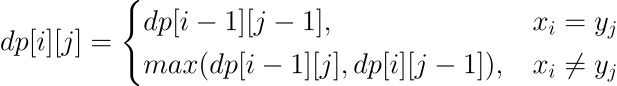
若i == 0或者 j == 0，则x或y其一是空串，最大公共序列是0

若x[i] == y[j]，那么在这个位置上的最优解 = 子串x[i-1]与子串y[j-1]的最长公共子序列 + 1

若x[i] != y[j]，则选择子串x[i-1]和子串y[i]的最长公共子序列与子串x[i]和子串y[j-1]的最长公共子序列的较大者

#include <iostream>
#include<string>
#include<algorithm>
using namespace std;

int main() {
	string x, y;
	cin >> x >> y;

	int** dp = new int*[x.length() + 1];
	for (unsigned int i = 0; i <= x.length(); ++i)
		dp[i] = new int[y.length() + 1];

	for(unsigned  int i = 0;i <= x.length();++i)
		for (unsigned  int j = 0; j <= y.length(); ++j){
			if (i == 0 || j == 0)  //初始化边界条件
				dp[i][j] = 0;
			else if (x[i - 1] == y[j - 1])  //string从0开始，dp从1开始
				dp[i][j] = dp[i - 1][j - 1] + 1;
			else
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
		}

	cout << dp[x.length()][y.length()] << endl;
        //以下是输出一条路径的具体节点
	//int i = x.length(), j = y.length();
	//do {
	//	if (dp[i][j] > dp[i - 1][j] && dp[i][j] > dp[i][j - 1])
	//	{
	//		cout <<x[i - 1]<<' ';  //cout <<y[j -1]<<' '
	//		--i;
	//		--j;
	//	}
	//	else if (dp[i - 1][j] > dp[i][j - 1])
	//		--i;
	//	else  //dp[i - 1][j] == dp[i][j - 1]也是这里
	//		--j; 
	//} while (i >= 0 && j >= 0);

	for (unsigned  int i = 0; i < y.length(); ++i)  //二维数组的释放
		delete[]dp[i];
	delete[] dp;
}

---

2020/8/16更

最长公共子串

最长公共子串与最长公共子序列的不同在于要求子串必须是连续的，那么状态转移方程就简化了许多，判断每一个位置字符相同的时候前一位是否也相同，填表的时候保存长度最大值。

#include <iostream>
#include<string>
#include<algorithm>
using namespace std;

int main() {
	string x, y ;
	int maxLen = 0;
	cin >> x >> y;

	int** dp = new int* [x.length() + 1];
	for (unsigned int i = 0; i <= x.length(); ++i)
		dp[i] = new int[y.length() + 1];

	for (unsigned int i = 0; i <= x.length(); ++i)
		for (unsigned int j = 0; j <= y.length(); ++j) {
			if (i == 0 || j == 0|| x[i] != y[j])  //初始化边界条件
				dp[i][j] = 0;
			else
			{
				dp[i][j] = dp[i - 1][j - 1] + 1;
				maxLen = max(maxLen, dp[i][j]);
			}
		}

	cout << maxLen << endl;

	for (unsigned int i = 0; i < y.length(); ++i)  //二维数组的释放
		delete[]dp[i];
	delete[] dp;
}