排序与复杂度分析

排序

桶排序

适用情况

元素值分布相对集中的序列（需要设计良好的映射规则）

排序过程
  1. 按映射规则，申请桶数组
  2. 遍历，将元素分到对应的桶
  3. 桶内排序
  4. 遍历，桶外合并
void bucketSort(int* arr, int len)
{
	int maximum = INT_MIN, minimum = INT_MAX;  //若保证arr全是非负数，可以简化映射规则
	int index;
	for (int i = 0; i < len; ++i) {
		maximum = max(maximum, arr[i]);
		minimum = min(minimum, arr[i]);
	}

	int bucketSize = (maximum - minimum) / 10 + 1;  //确保把最小数映射到下标为0
	vector<int>* bucket = new vector<int>[bucketSize];

	for (int i = 0; i < len; i++)  //数组入桶
	{
		index = arr[i] / 10 - minimum / 10 + 1;
		bucket[index].emplace_back(arr[i]);
	}

	for (int i = 0; i < bucketSize; ++i)  //桶内排序
		if (!bucket[i].empty())
			sort(bucket[i].begin(), bucket[i].end());

	index = 0;
	for (int i = 0; i < bucketSize; ++i)  //桶写回数组
		for (int j = 0; j < bucket[i].size(); ++j)
			arr[index++] = bucket[i][j];

	delete []bucket;
	bucket = nullptr;
}
说明
  • 若映射规则过松，元素集中在单桶内，则排序算法退化成桶内比较排序算法
  • 若映射规则过紧，每个元素分布在不同的桶上，排序算法退化成计数排序
  • 稳定性取决于桶内的排序算法

插入排序

适用情况

数据量小，或基本有序

排序思路（整体而言是往一个新的有序的序列中插入新的元素直到所有元素有序）
  1. 下标从小到大，遍历数组
  2. 比较相邻的两个元素是否符合规则，不符合则交换，继续内循环，若符合则退到外循环。
template<class T>
void insertSort(T* arr, int len, bool flag) {  //插入排序
	for (int i = 1; i < len; ++i)
		for (int j = i - 1; j >= 0 && compare(arr[j + 1], arr[j], flag); --j)
			swap(arr[j + 1], arr[j]);
	return;
}
  • 说明：

compare函数是为了支持升序，降序两种排序方式

template<class T>
bool compare(const T& x, const T& y, bool flag) {  //引用传递不产生临时对象
	if (flag)
		return x < y;
	else
		return x > y;
}
动态排序过程

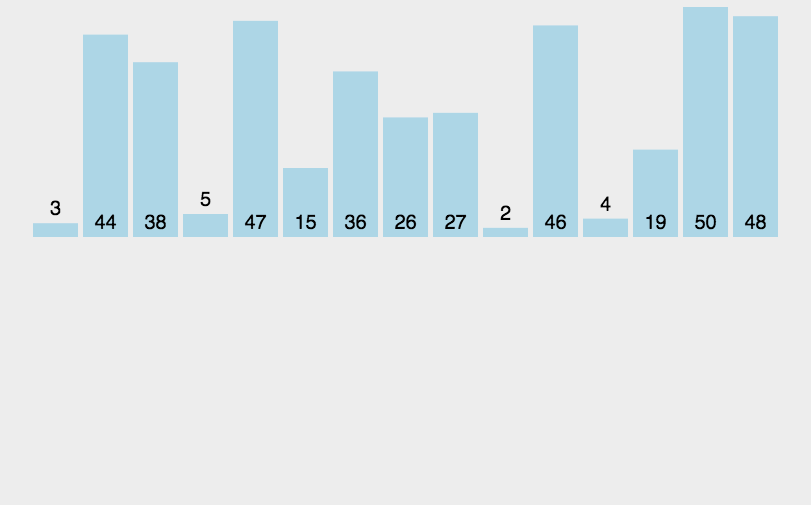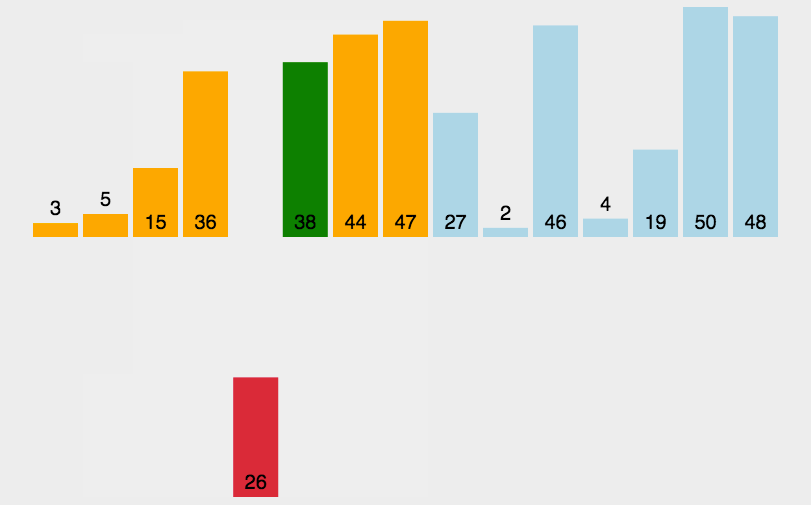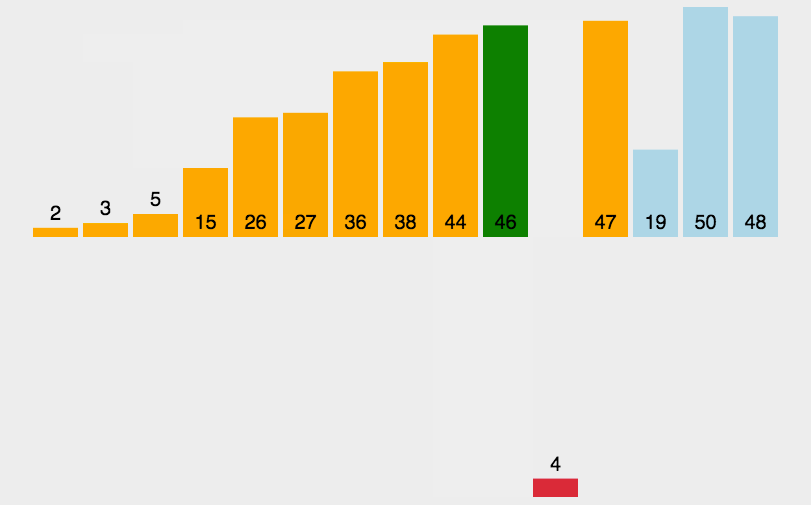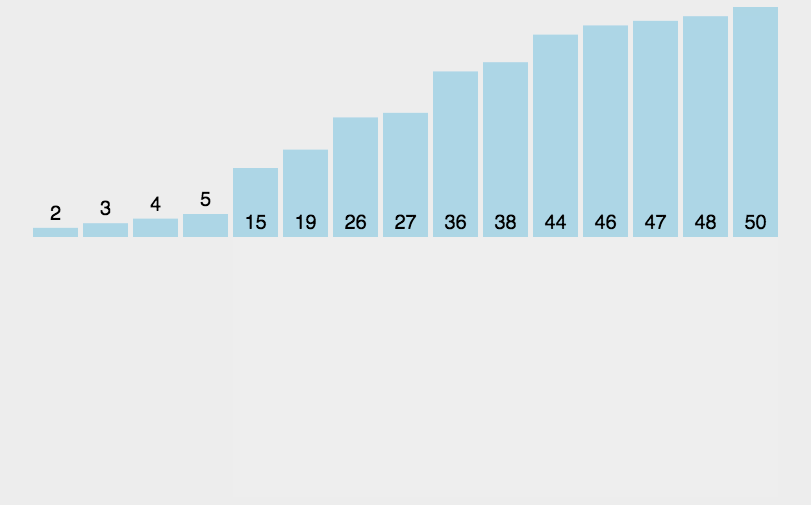
希尔排序

适用情况

同插入排序

排序思路

在插入排序外加一层循环，设定间隔将元素分组，组内插入排序。（下一次粒度更小的分组排序时元素相对有序）

template<class T>
void shellSort(T* arr, int len, bool flag) {  //希尔排序

	for (int gap = len / 2; gap > 0; gap /= 2)  //shell增量序列
		for (int i = gap; i < len; ++i)
			for (int j = i - gap; j >= 0 && compare(arr[j + gap], arr[j], flag); j -= gap)
				swap(arr[j + gap], arr[j]);
	//int k = 1;
	//while (pow(2, k) - 1 < len)
	//	++k;
	//while (int gap = static_cast<int>(pow(2, k) - 1) > 0) {  //Hibbard增量序列
	//	for (int i = gap; i < len; ++i) {
	//		for (int j = i - gap; j >= 0 && compare(arr[j + gap], arr[j], flag); j -= gap)
	//			swap(arr[j + gap], arr[j]);
	//	}
	//	--k;
	//}
	return;
}

冒泡排序

适用情况

排序效率倒数第一，而且当元素逆序时效果最差。

排序思路（每次选择最大（最小）的元素置于末尾）
  1. 外循环遍历数组
  2. 内循环比较相邻的元素，若不符合则发生交换

基础版

template<class T>
void bubbleSort(T* arr, int len, bool flag)
{
	for (int i = 1; i < len; ++i) {
		for (int j = 0; j < len - i; ++j) {  //从后往前，每次循环把第k小的数放在k的位置上
			if (compare(arr[j + 1], arr[j], flag)) 
				swap(arr[j], arr[j + 1]);
		}
		//printArray(arr, 6);
	}
}

改进版：当序列已有序时不再排序（收效甚微）

template<class T>
void bubbleSort(T* arr, int len, bool flag)
{
	for (int i = 1; i < len; ++i) {
		bool exchange = false;  //是否当已经有序
		for (int j = 0; j < len -i; ++j) {  //从后往前，每次循环把第k小的数放在k的位置上
			if (compare(arr[j + 1], arr[j], flag)) {
				swap(arr[j], arr[j + 1]);
				exchange = true;
			}
		}
		printArray(arr, 6);
		if (!exchange)
			return;
	}
}
动态排序过程

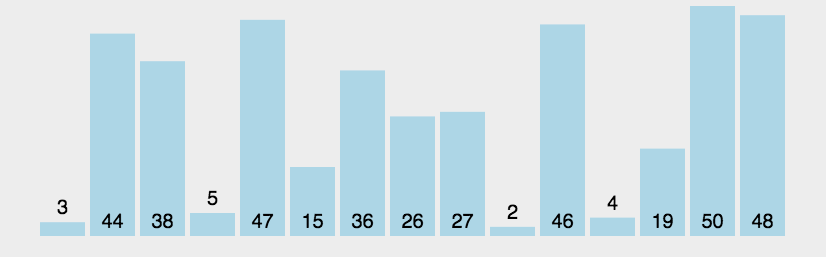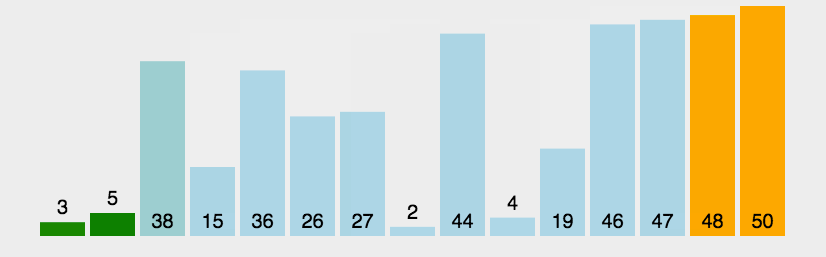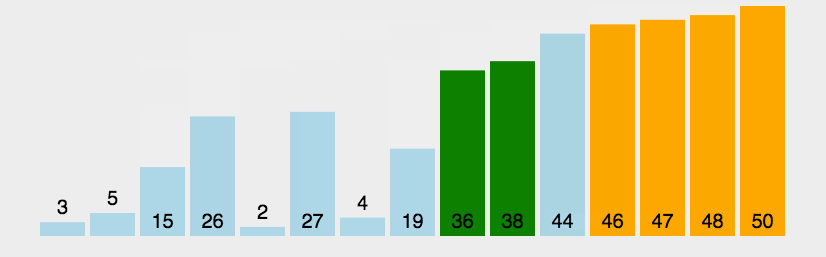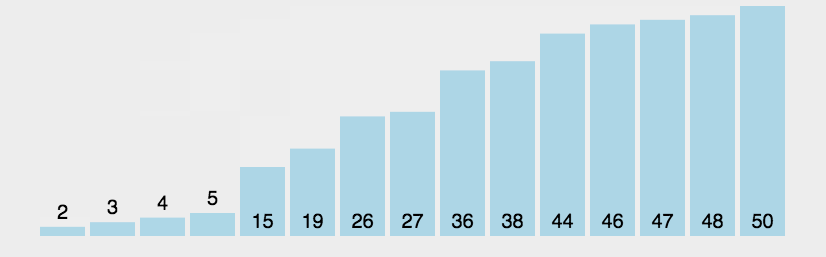
快速排序

适用情况

大多数情况下第一名

排序思路(冒泡基础之上的分治递归)
  1. 将序列划分为左右序列，递归
  2. 划分中，以最左元素为支点，从右向左选择小于支点覆盖到左序列，从左到右选择大于支点覆盖到右序列，直到序列下标相遇，返回相遇的下标。
template<class T>
int quickSortPartition(T* arr, int left, int right) {  //交替覆盖
	int l = left, r = right, x = arr[left];
	while (l < r)
	{
		while (l < r && arr[r] >= x)  //从右向左寻找第一个小于x的数,不必考虑越界
			--r;
		if (l < r)
			arr[l++] = arr[r];  //替换左元素
		while (l < r && arr[l] <= x)  //从左向右寻找第一个大于x的数，不必考虑越界
			++l;
		if (l < r)
			arr[r--] = arr[l];  //替换右元素
	}
	arr[l] = x;  //写回支点元素，可能导致不稳定
	return l;
}
template<class T>
void quickSort(T* arr, int left, int right) {
	if (left >= right)
		return;
	int benchmark = quickSortPartition(arr, left, right);
	quickSort(arr, left, benchmark - 1);
	quickSort(arr, benchmark + 1, right);
}

输入序列为7，3，8，5，1，2时执行情况如下

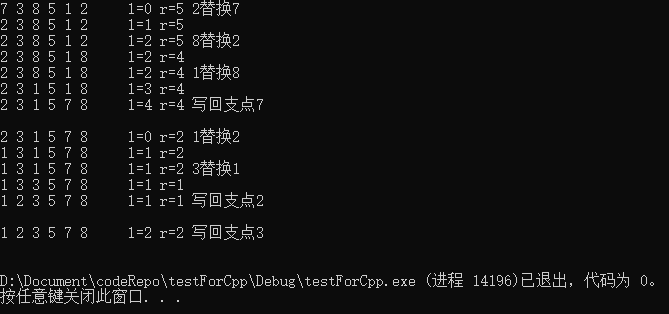
动态排序过程

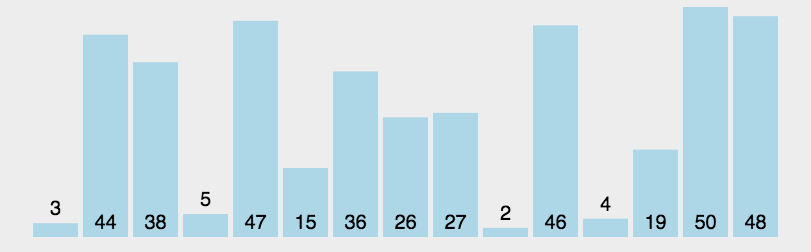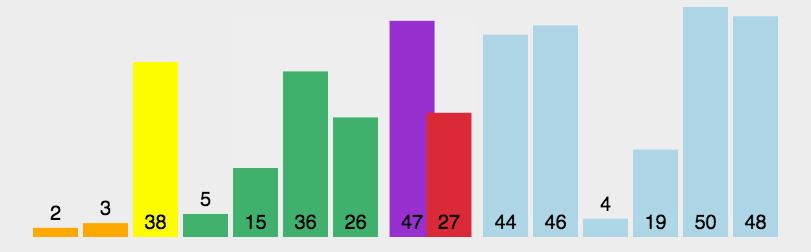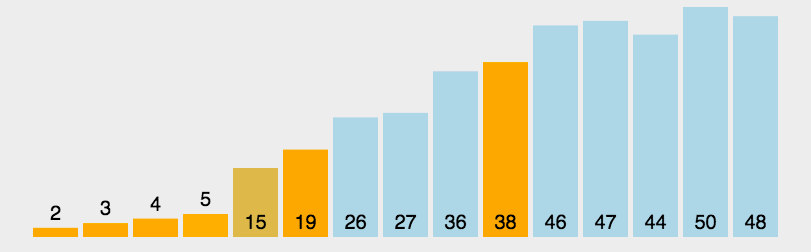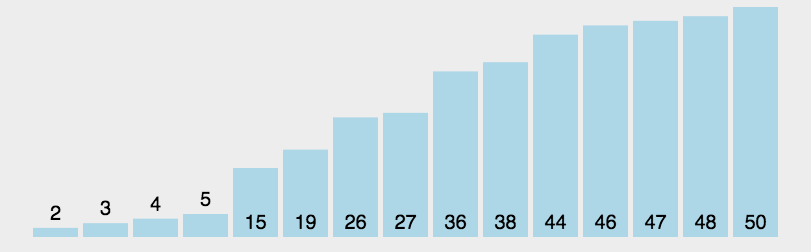
归并排序

适用情况

适合外部排序

排序思路
  1. 二路归并将序列两两划分，递归直到最后只有序列只有单个元素（分）
  2. 将相邻序列两两合并，直到合成一个序列（治）
template<class T>
void merge(vector<T>& arr, int left, int mid, int right) {  //治

	vector<T> temp;  //临时数组空间
	temp.resize(right - left + 1);
	int i = left;  // i是左序列的下标
	int j = mid + 1;  // j是右序列的下标
	int t = 0;  // t是临时数组的下标

	while (i <= mid && j <= right) {  //扫描直到有序列结束
		if (arr[i] <= arr[j]) {  //左序列小，左序列下标为i的值写入临时数组
			temp[t++] = arr[i++];
		}
		else {  //右序列小，右序列下标为j的值写入临时数组
			temp[t++] = arr[j++];
		}
	}
	while (i <= mid) {  //若左序列未扫描完，余下写入临时数组
		temp[t++] = arr[i++];
	}

	while (j <= right) {  //若右序列未扫描完，余下写入临时数组
		temp[t++] = arr[j++];
	}

	t = 0;  //重置临时数组下标
	while (left <= right) {  // 将临时数组回写到原序列中
		arr[left++] = temp[t++];
	}
}

template<class T>
void mergeSort(vector<T>& arr, int left, int right) {  //分
	if (left < right) {  //当left=right时已经时只有一个元素
		int mid = (left + right) / 2;
		mergeSort(arr, left, mid);
		mergeSort(arr, mid + 1, right);  //当left+right是奇数时，左边多分一个
		merge(arr, left, mid, right);
	}
}
动态排序过程

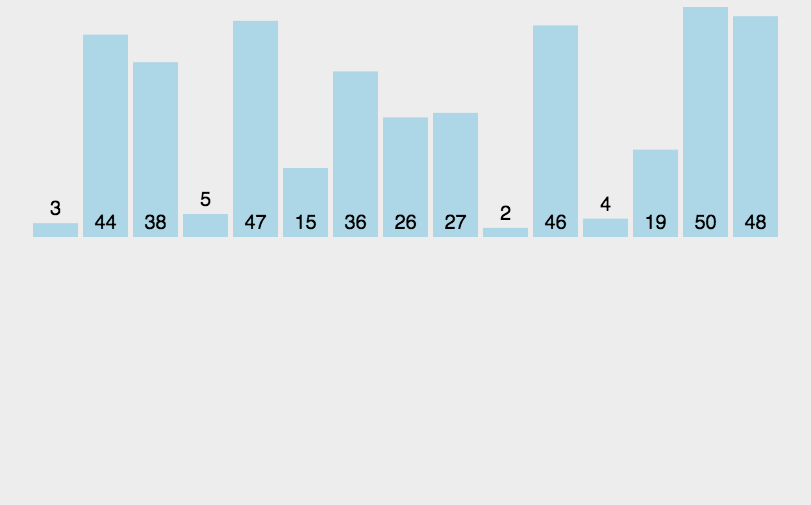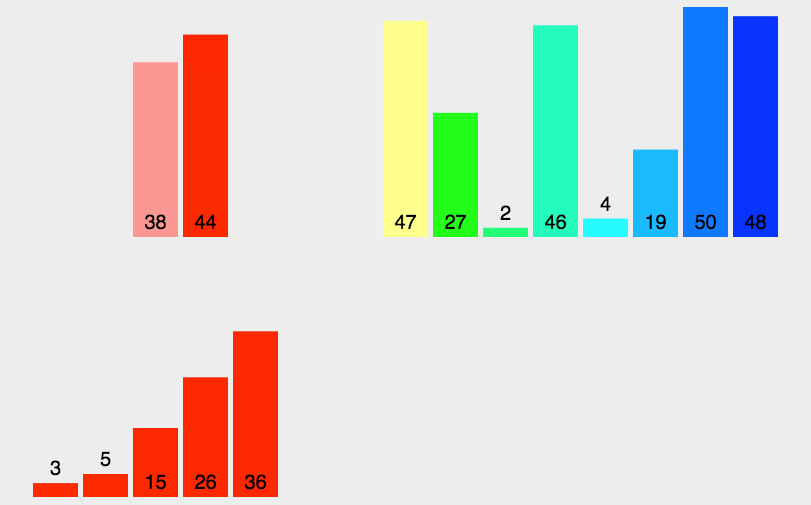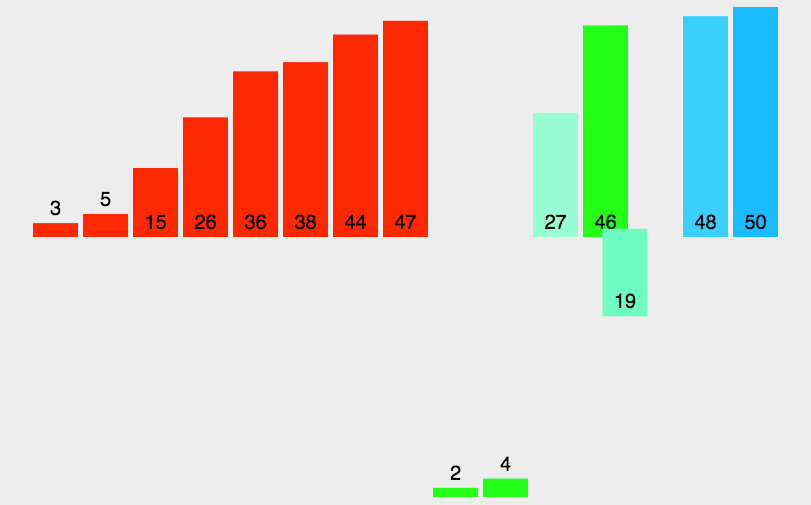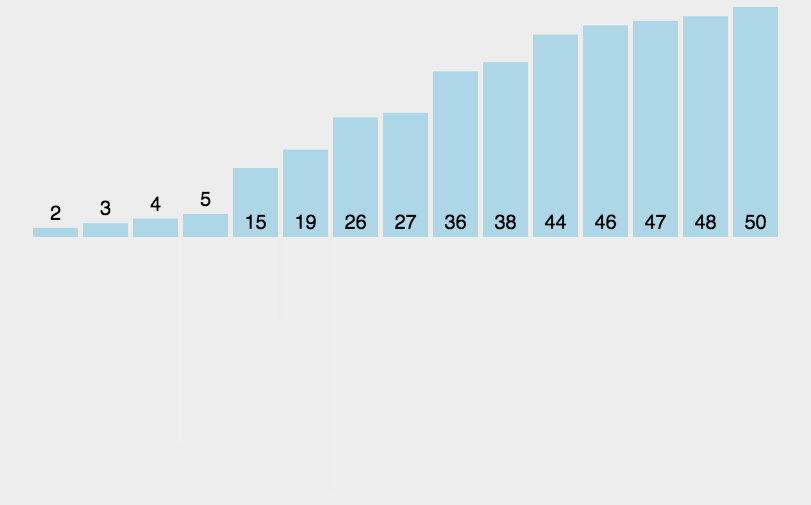
选择排序

适用情况

只需要Top的数据

排序原理

两趟循环，每次最小记录的下标，第k遍将第k小的数放在k的位置上

template<class T>
void selectSort(T* arr, int len, bool flag)
{
	for (int i = 0; i < len; ++i) {
		int index = i;
		for (int j = i + 1; j < len; ++j) {  //每次选择最小的放在最前面
			if (compare(arr[j], arr[index], flag))
				index = j;
		}
        if(i != index)
		swap(arr[i], arr[index]);
	}
}
动态排序过程

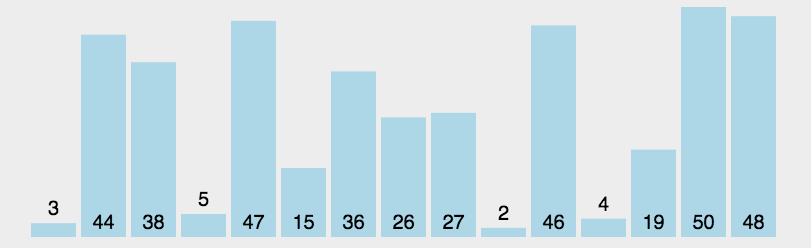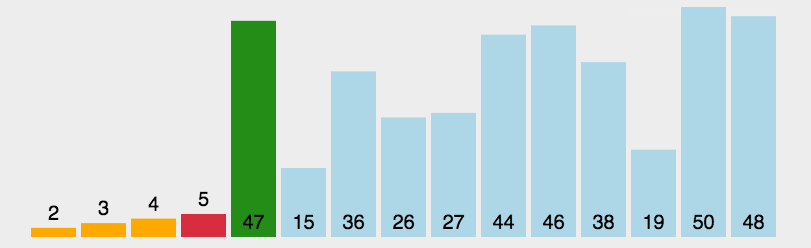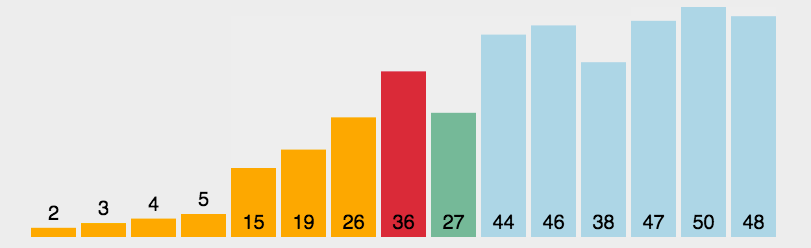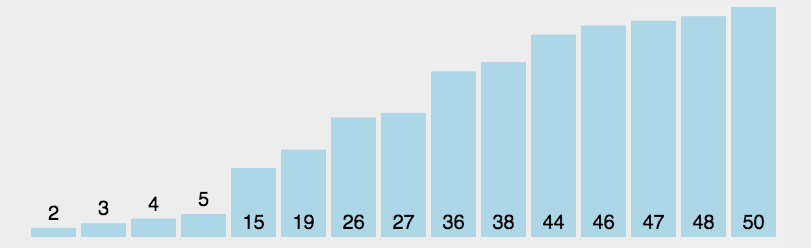
堆排序

堆的实现blog

时空复杂度及稳定性

排序算法 平均时间复杂度 最坏时间复杂度 最好时间复杂度 空间复杂度 稳定性
桶排序 O(M+N)
插入排序 O(N2) O(N2) O(N) O(1) 稳定
希尔排序 O(1) 不稳定
冒泡排序 O(N2) O(N2) O(N) O(1) 稳定
快速排序 O(Nlog2N) O(N2) O(Nlog2N) O(Nlog2N) 不稳定
归并排序 O(Nlog2N) O(Nlog2N) O(Nlog2N) O(N) 稳定
选择排序 O(N2) O(N2) O(N2) O(1) 不稳定
堆排序 O(Nlog2N) O(Nlog2N) O(Nlog2N) O(1) 不稳定
说明：
  1. 桶排序的复杂度与稳定性依赖于桶内排序的实现，希尔排序的复杂度依赖于增量序列的选择
  2. 允许跨越式Swap操作的排序算法是不稳定的。
posted @ 2020-08-05 17:50  kite97  阅读(163)  评论(0)  编辑  收藏  举报