谈平衡二叉树的原理（c++实现）

Self-Balancing Binary Search Tree

定义

任意节点子树的高度差（称为平衡因子）不超过1。

节点结构体：

template<class T>
struct Node {
	T key;
	Node<T>* lchild;
	Node<T>* rchild;
	Node<T>(T k) : key(k), lchild(nullptr), rchild(nullptr) {}
};

平衡二叉树类：

template<class T>
class AVLTree {
private:
	Node<T>* root;
public:
	AVLTree() :root(nullptr) {};
	Node<T>* getRoot() { return root; }
	void printTree();
	Node<T>* llRotation(Node<T>*);
	Node<T>* lrRotation(Node<T>*);
	Node<T>* rrRotation(Node<T>*);
	Node<T>* rlRotation(Node<T>*);
	void balance(Node<T>*);
	void insert(const T&);
	bool remove(Node<T>*, Node<T>*, T);
	int getDepth(Node<T>*);
	int getBalanceFactor(Node<T>*);
	Node<T>* findMin(Node<T>*);
	Node<T>* findMax(Node<T>*);
	void fixUp();  //修复平衡
	Node<T>* find(Node<T>* node, T key);
};

操作

二叉平衡树与二叉排序树非常相似，以下重点谈谈树的自平衡策略。

左旋的动态过程：

右旋的动态过程：

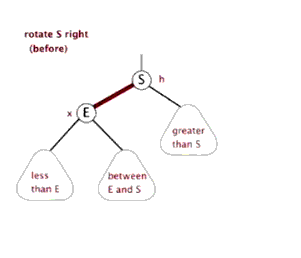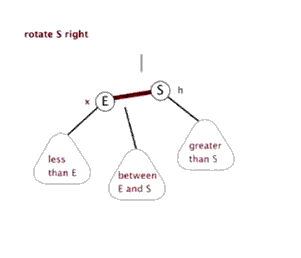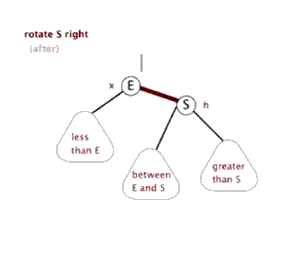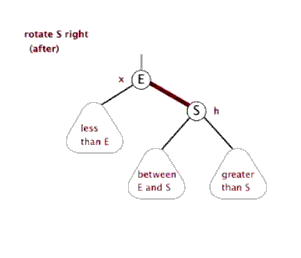
ll型（右旋）

插入或者删除导致某节点a失衡（平衡因子绝对值大于1）,而且a的左子树b（a->lchild）的左子树c(b->lchild)比右子树d(b->rchild)高。对a节点作ll平衡。

template<class T>
Node<T>* AVLTree<T>::llRotation(Node<T>* node) {  //插入节点在左子树左边，右旋
	Node<T>* temp = node->lchild;
	node->lchild = temp->rchild;
	temp->rchild = node;
	return temp;
}

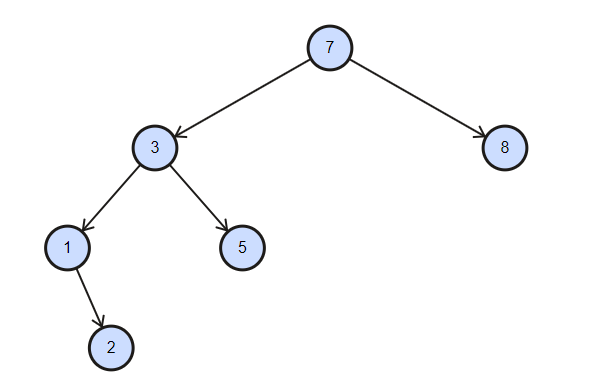
lr型

插入或者删除导致某节点a失衡（平衡因子绝对值大于1）,而且a的左子树b（a->lchild）的左子树c(b->lchild)比右子树d(b->rchild)矮。对b节点作rr平衡，再对a作ll平衡。

template<class T>
Node<T>* AVLTree<T>::lrRotation(Node<T>* node) {  //插入节点在左子树右边
	Node<T>* temp = node->lchild;
	node->lchild = rrRotation(temp);
	return llRotation(node);
}

rr型

与ll型对称

rl型

与lr型对称

平衡策略

自顶向下查找失衡节点，根据平衡因子的情况作平衡处理。总体而言，是将节点从树高的一侧借调到树低的一侧。（如果Node中有parent指针的话可以自底向上，从插入或删除节点开始寻找失衡节点）

template<class T>
void AVLTree<T>::balance(Node<T>* node) {
	int bf = getBalanceFactor(node);  //平衡因子
	if (bf > 1) {  //失衡，左高
		if (getBalanceFactor(node->lchild) > 0)  //左左高，ll
			root = llRotation(node);
		else  //左右高,lr
			root = lrRotation(node);
	}
	else if (bf < -1) {  //失衡，右高
		if (getBalanceFactor(node->rchild) > 0)  //右左高,rl
			root = rlRotation(node);
		else
			root = rrRotation(node);  //右边高,rr
	}
	return;
}

源码

#include<iostream>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;

template<class T>
struct Node {
	T key;
	Node<T>* lchild;
	Node<T>* rchild;
	Node<T>(T k) : key(k), lchild(nullptr), rchild(nullptr) {}
};

template<class T>
class AVLTree {
private:
	Node<T>* root;
public:
	AVLTree() :root(nullptr) {};
	Node<T>* getRoot() { return root; }
	void printTree();
	Node<T>* llRotation(Node<T>*);
	Node<T>* lrRotation(Node<T>*);
	Node<T>* rrRotation(Node<T>*);
	Node<T>* rlRotation(Node<T>*);
	void balance(Node<T>*);
	void insert(const T&);
	bool remove(Node<T>*, Node<T>*, T);
	int getDepth(Node<T>*);
	int getBalanceFactor(Node<T>*);
	Node<T>* findMin(Node<T>*);
	Node<T>* findMax(Node<T>*);
	void fixUp();
	Node<T>* find(Node<T>* node, T key);
};

template<class T>
void AVLTree<T>::printTree() {  //层次遍历
	Node<T>* pos = root;  //当前位置
	Node<T>* flag = root;  //层末标识

	queue<Node<T>*> q;
	q.push(root);  //根节点入队

	while (!q.empty()) {  //队列非空
		Node<T>* node = q.front();
		q.pop();  //弹出队首
		cout << node->key << '\t';

		if (node->lchild != nullptr) {  //左孩子非空则入队
			q.push(node->lchild);
			pos = node->lchild;
		}

		if (node->rchild != nullptr) {  //右孩子非空则入队
			q.push(node->rchild);
			pos = node->rchild;
		}

		if (node == flag) {  //抵达层末
			flag = pos;
			cout << "\n";
		}
	}
}

template<class T>
void AVLTree<T>::insert(const T& key) {
	Node<T>* node = new Node<T>(key);
	if (root == nullptr) {
		root = node;
		return;
	}
	Node<T>* pos = root;
	while (true) {  //查找插入位置
		if (node->key < pos->key) {
			if (pos->lchild == nullptr) {
				pos->lchild = node;
				fixUp();
				return;
			}   //end if
			else
				pos = pos->lchild;
		}  //end if
		else if (node->key > pos->key) {
			if (pos->rchild == nullptr) {
				pos->rchild = node;
				fixUp();
				return;
			}  //end if
			else
				pos = pos->rchild;
		}  //end if
		else
			return;  //树中已有此节点则无操作
	}  //end while
}

template<class T>
int AVLTree<T>::getDepth(Node<T>* node) {
	if (node == nullptr)
		return 0;
	return max(getDepth(node->lchild), getDepth(node->rchild)) + 1;
}

template<class T>
int AVLTree<T>::getBalanceFactor(Node<T>* node) {  //平衡因子 = 左子树高-右子树高
	return getDepth(node->lchild) - getDepth(node->rchild);
}

template<class T>
void AVLTree<T>::balance(Node<T>* node) {
	int bf = getBalanceFactor(node);
	if (bf > 1) {
		if (getBalanceFactor(node->lchild) > 0)
			root = llRotation(node);
		else
			root = lrRotation(node);
	}
	else if (bf < -1) {
		if (getBalanceFactor(node->rchild) > 0)
			root = rlRotation(node);
		else
			root = rrRotation(node);
	}
	return;
}

template<class T>
Node<T>* AVLTree<T>::llRotation(Node<T>* node) {  //插入节点在左子树左边，右旋
	Node<T>* temp = node->lchild;
	node->lchild = temp->rchild;
	temp->rchild = node;
	return temp;
}

template<class T>
Node<T>* AVLTree<T>::lrRotation(Node<T>* node) {  //插入节点在左子树右边
	Node<T>* temp = node->lchild;
	node->lchild = rrRotation(temp);
	return llRotation(node);
}

template<class T>
Node<T>* AVLTree<T>::rlRotation(Node<T>* node) {  //插入节点在右子树左边
	Node<T>* temp = node->rchild;
	node->rchild = llRotation(temp);
	return rrRotation(node);
}

template<class T>
Node<T>* AVLTree<T>::rrRotation(Node<T>* node) {  //插入节点在右子树左边，左旋
	Node<T>* temp = node->rchild;
	node->rchild = temp->lchild;
	temp->lchild = node;
	return temp;
}

template<class T>
bool AVLTree<T>::remove(Node<T>* node, Node<T>* parent, T key) {
	Node<T>* temp = nullptr;
	if (node == nullptr)  // 未找到目标节点
		return false;
	else if (key < node->key)
		return remove(node->lchild, node, key);
	else if (key > node->key)
		return remove(node->rchild, node, key);
	else if (node->lchild && node->rchild) {  //删除节点有左子树也有右子树

		if (getDepth(node->lchild) > getDepth(node->rchild)) {  //左子树高，前驱替代
			temp = findMax(node->lchild);
			node->key = temp->key;
			return remove(node->lchild,node, node->key);
		}
		else {  //右子树不比左子树矮，后驱替代
			temp = findMin(node->rchild);
			node->key = temp->key;
			return remove(node->rchild, node, node->key);
		}
	}
	else {
		if ((node->lchild && node->rchild == nullptr)) {  //删除节点有左孩子无右孩子
			temp = findMax(node->lchild);
			node->key = temp->key;
			return remove(node->lchild, node, node->key);
		}
		else if (node->rchild && node->lchild == nullptr) {  //删除节点有右孩子无左孩子
			temp = findMin(node->rchild);
			node->key = temp->key;
			return remove(node->rchild, node, node->key);
		}  //end if
		else {  //删除节点最终递归到删除叶子节点
			if (node == parent->lchild)  //父节点指针置空
				parent->lchild = nullptr;
			else
				parent->rchild = nullptr;
			delete node;  //释放子节点
			node = nullptr;

			fixUp();
		}
	}  //end else
	return true;
}

template<class T>
void AVLTree<T>::fixUp() {
	Node<T>* temp = this->root;  //自顶向下调整树
	while (1)  //寻找失衡的节点
	{
		if (getBalanceFactor(temp) == 2) {
			if (fabs(getBalanceFactor(temp->lchild)) == 1)
				break;
			else
				temp = temp->lchild;
		}
		else if (getBalanceFactor(temp) == -2) {
			if (fabs(getBalanceFactor(temp->rchild)) == 1)
				break;
			else
				temp = temp->rchild;
		}
		else break;
	}
	balance(temp);
	return;
}

template<class T>
Node<T>* AVLTree<T>::find(Node<T>* node, T key) {
	while (node != nullptr && key != node->key) {  //迭代查找
		if (key < node->key)
			node = node->lchild;
		else
			node = node->rchild;
	}
	if (node == nullptr)
		cout << "Element " << key << " doesn't exist!" << endl;
	else
		cout << "Element " << key << " exists." << endl;
	return node;
}

template<class T>
Node<T>* AVLTree<T>::findMax(Node<T>* node) {
	if (node != nullptr) {
		while (node->rchild)
			node = node->rchild;
	}
	return node;
}

template<class T>
Node<T>* AVLTree<T>::findMin(Node<T>* node) {
	if (node != nullptr) {
		if (node->lchild == nullptr)  //左孩子为空，当前节点已是最左下
			return node;
		else
			return findMin(node->lchild);  //左孩子不为空，往左子树遍历
	}
	else
		return nullptr;  //空树返回nullptr
}

int main() {
	int arr[]{ 7,4,8,5,1,6};//ll:738512建树;rr:7385129删除2;rl:7385124删除4;lr:748516建树
	AVLTree<int> avl;
	for (int i = 0; i < 6; i++)
	{
		avl.insert(arr[i]);
	}
	avl.printTree();
	avl.find(avl.getRoot(),8);
	avl.remove(avl.getRoot(), nullptr, 8);
	avl.printTree();
}