简析二叉排序树（c++实现）

Binary Search Tree

定义

每一个节点的值大于其左子树（若存在）任意节点，小于其右子树（若存在）任意节点。

节点结构体：

 template<class T>
 struct Node {  //节点结构体
   T key;  
   Node<T>* lchild;
   Node<T>* rchild;
   Node(T k) :key(k), lchild(nullptr), rchild(nullptr) {}
 };

二叉排序树类：功能包括增删查和两种遍历

 template<class T>
 class BinarySortTree {
 private:
   Node<T>* root;
 public:
   BinarySortTree() :root(nullptr) {}
   Node<T>* getRoot() { return root; }
   void insert(T);
   bool remove(Node<T>*, Node<T>*,T);
   Node<T>* findMax(Node<T>*);
   Node<T>* findMin(Node<T>*);
   Node<T>* find(Node<T>*, T);
   int getDepth(Node<T>*);
   void inOrderTraversal(Node<T>*);
   void printTree();  //层次遍历
 };

操作

构造

插入新节点：

判断根节点是否为空
从根开始，若插入值大于当前位置的的键值，向右子树迭代，否则向左子树迭代。迭代边界是叶子节点，将新节点插入到叶子节点中
对重复的键值不作处理

template<class T>
 void BinarySortTree<T>::insert(T key) {
   Node<T>* node = new Node<T>(key);
   if (root == nullptr) {   //若根为空，插入根
     root = node;
     return;
   }
   Node<T>* pos = root;
   while (true) {  //查找插入位置
     if (node->key < pos->key) {
       if (pos->lchild == nullptr) {
         pos->lchild = node;
         return;
       }
       else
         pos = pos->lchild;
     }
     else if (node->key > pos->key) {
       if (pos->rchild == nullptr) {
         pos->rchild = node;
         return;
       }
       else
         pos = pos->rchild;
     }
     else
       return;  //树中已有此节点则无操作
   }
 }

复杂度

O(log2N)~O(N)

对严格有序的输入，二叉排序树会退化成类似链表的结构。

查找

有递归和迭代两个实现方式，下列是迭代查找。
- 当节点不为空且键值未匹配时，循环迭代
- 若树为空或迭代查找到叶子的孩子，查找失败；否则查找成功
- 返回查找到的节点，若未匹配，返回nullptr

 template<class T>
 Node<T>* BinarySortTree<T>::find(Node<T>* node, T key) {
   while (node != nullptr && key != node->key) {  //迭代查找
     if (key < node->key)
       node = node->lchild;
     else
       node = node->rchild;
   }
   if (node == nullptr)  
     cout << "Element " << key << " doesn't exist!" << endl;
   else
     cout << "Element " << key << " exists." << endl;
   return node;  //返回查找的节点
 }

删除

递归直到找到被删除节点
若删除节点是叶子节点，则直接删除（断开叶子节点和其父节点的连接，使得remove函数传入了3个参数，另一种做法是在Node节点类里增加parent指针，若读者有较优雅的做法，恳求与我分享）
若删除节点只有左孩子，前驱替代，只有右孩子，后继替代
若既有有孩子又有左孩子，则用前驱节点（或后继节点）替代当前节点，删除前驱节点（或后继节点）

 template<class T>
 bool BinarySortTree<T>::remove(Node<T>* node,Node<T>* parent,T key) {
   Node<T>* temp = nullptr;
   if (node == nullptr)  // 未找到目标节点
     return false;
   else if (key < node->key)
     return remove(node->lchild,node, key);
   else if (key > node->key)
     return remove(node->rchild,node, key);
   else if (node->lchild && node->rchild) {  //删除节点有左子树也有右子树
     temp = findMin(node->rchild);
     node->key = temp->key;
     return remove(node->rchild,node, node->key);
   }
   else {
     if ((node->lchild && node->rchild == nullptr)) {  //删除节点有左孩子无右孩子
       temp = findMax(node->lchild);
       node->key = temp->key;
       return remove(node->lchild,node, node->key);
     }
     else if (node->rchild && node->lchild == nullptr) {  //删除节点有右孩子无左孩子
       temp = findMin(node->rchild);
       node->key = temp->key;
       return remove(node->rchild,node, node->key);
     }  //end if
     else {  //删除节点最终递归到删除叶子节点
       if (node == parent->lchild)  //父节点置空
         parent->lchild = nullptr;
       else
         parent->rchild = nullptr;
       delete node;  //释放子节点
       node = nullptr;
     }
   }  //end else
   return true;
 }

关于删除的几点说明：

为什么是前驱/后继节点？

因为前驱节点或者后继节点作替代，不会破坏二叉排序树的结构特性。将二叉树投影到x轴上可以发现，离删除节点最近的节点正是其前驱/后继。

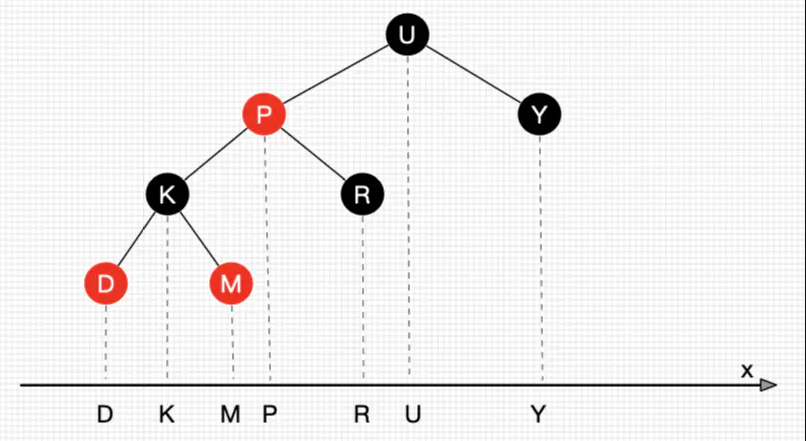
二叉排序树的x轴投影

删除的过程最终都会递归到对叶子的节点的操作，断开叶子节点与其父节点的连接。

例如删除节点3，首先将后继节点5的键值覆盖节点3的键值，然后在原节点3的右子树上递归删除键值为5的节点。

输入序列为3，7，8，5，1，2

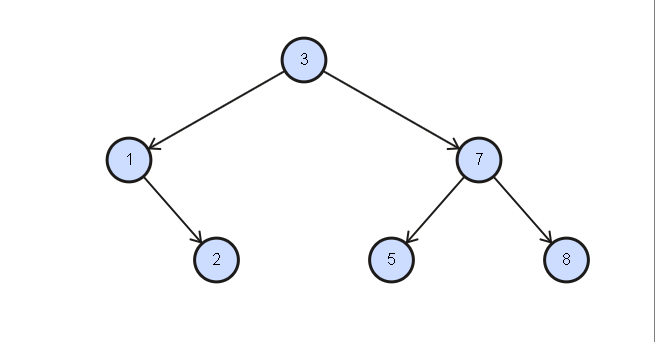
测试代码

#include<iostream>
#include<queue>
using namespace std;

template<class T>
struct Node {  //节点结构体
    T key;
    Node<T>* lchild;
    Node<T>* rchild;
    Node(T k) :key(k), lchild(nullptr), rchild(nullptr) {}
};

template<class T>
class BinarySortTree {
private:
    Node<T>* root;
public:
    BinarySortTree() :root(nullptr) {}
    Node<T>* getRoot() { return root; }
    void insert(T);
    bool remove(Node<T>*, Node<T>*,T);
    Node<T>* findMax(Node<T>*);
    Node<T>* findMin(Node<T>*);
    Node<T>* find(Node<T>*, T);
    int getDepth(Node<T>*);
    void inOrderTraversal(Node<T>*);
    void printTree();
};

template<class T>
void BinarySortTree<T>::insert(T key) {
    Node<T>* node = new Node<T>(key);
    if (root == nullptr) {
        root = node;
        return;
    }
    Node<T>* pos = root;
    while (true) {  //查找插入位置
        if (node->key < pos->key) {
            if (pos->lchild == nullptr) {
                pos->lchild = node;
                return;
            }   //end if
            else
                pos = pos->lchild;
        }  //end if
        else if (node->key > pos->key) {
            if (pos->rchild == nullptr) {
                pos->rchild = node;
                return;
            }  //end if
            else
                pos = pos->rchild;
        }  //end if
        else
            return;  //树中已有此节点则无操作
    }  //end while
}

template<class T>
Node<T>* BinarySortTree<T>::find(Node<T>* node, T key) {
    while (node != nullptr && key != node->key) {  //迭代查找
        if (key < node->key)
            node = node->lchild;
        else
            node = node->rchild;
    }
    if (node == nullptr)
        cout << "Element " << key << " doesn't exist!" << endl;
    else
        cout << "Element " << key << " exists." << endl;
    return node;
}

template<class T>
Node<T>* BinarySortTree<T>::findMax(Node<T>* node) {
    if (node != nullptr) {
        while (node->rchild)
            node = node->rchild;
    }
    return node;
}

template<class T>
Node<T>* BinarySortTree<T>::findMin(Node<T>* node) {
    if (node != nullptr) {
        if (node->lchild == nullptr)  //左孩子为空，当前节点已是最左下
            return node;
        else
            return findMin(node->lchild);  //左孩子不为空，往左子树遍历
    }
    else
        return nullptr;  //空树返回nullptr
}

template<class T>
int BinarySortTree<T>::getDepth(Node<T>* node) {
    return node == nullptr ? 0 : max(getDepth(node->lchild), getDepth(node->rchild) + 1);
}


template<class T>
void BinarySortTree<T>::inOrderTraversal(Node<T>* node) {  //中序遍历
    if (node != nullptr) {
        inOrderTraversal(node->lchild);
        cout << node->key << ' ';
        inOrderTraversal(node->rchild);
    }
}

template<class T>
bool BinarySortTree<T>::remove(Node<T>* node,Node<T>* parent,T key) {
    Node<T>* temp = nullptr;
    if (node == nullptr)  // 未找到目标节点
        return false;
    else if (key < node->key)
        return remove(node->lchild,node, key);
    else if (key > node->key)
        return remove(node->rchild,node, key);
    else if (node->lchild && node->rchild) {  //删除节点有左子树也有右子树
        temp = findMin(node->rchild);
        node->key = temp->key;
        return remove(node->rchild,node, node->key);
    }
    else {
        if ((node->lchild && node->rchild == nullptr)) {  //删除节点有左孩子无右孩子
            temp = findMax(node->lchild);
            node->key = temp->key;
            return remove(node->lchild,node, node->key);
        }
        else if (node->rchild && node->lchild == nullptr) {  //删除节点有右孩子无左孩子
            temp = findMin(node->rchild);
            node->key = temp->key;
            return remove(node->rchild,node, node->key);
        }  //end if
        else {  //删除节点最终递归到删除叶子节点
            if (node == parent->lchild)  //父节点置空
                parent->lchild = nullptr;
            else
                parent->rchild = nullptr;
            delete node;  //释放子节点
            node = nullptr;
        }
    }  //end else
    return true;
}

template<class T>
void BinarySortTree<T>::printTree() {  //层次遍历
    Node<T>* pos = root;  //当前位置
    Node<T>* flag = root;  //层末标识

    queue<Node<T>*> q;
    q.push(root);  //根节点入队

    while (!q.empty()) {  //队列非空
        Node<T>* node = q.front();
        q.pop();  //弹出队首
        cout << node->key << '\t';

        if (node->lchild != nullptr) {  //左孩子非空则入队
            q.push(node->lchild);
            pos = node->lchild;
        }

        if (node->rchild != nullptr) {  //右孩子非空则入队
            q.push(node->rchild);
            pos = node->rchild;
        }

        if (node == flag) {  //抵达层末
            flag = pos;
            cout << "\n";
        }
    }
}

int main()
{
    //               9
    //      5           14
    //  1     7      10     18
    //          8       15     20

    int arr[10]{ 9,5,14,1,7,18,15,10,8,20 };
    BinarySortTree<int> bst;
    for (int i : arr)
        bst.insert(i);  //注意是for循环不是迭代器
    bst.printTree();

    cout << "Max element:" << bst.findMax(bst.getRoot())->key << endl;
    cout << "Min element:" << bst.findMin(bst.getRoot())->key << endl;
    cout << "Tree depth:" << bst.getDepth(bst.getRoot()) << endl;

    bst.find(bst.getRoot(), 15)->key;
    bst.remove(bst.getRoot(),nullptr,20);
    bst.inOrderTraversal(bst.getRoot());
    cout << endl;
    bst.printTree();
}

posted @ 2020-08-03 23:36 kite97 阅读(356) 评论(0) 编辑收藏举报

刷新页面返回顶部

kite97

简析二叉排序树（c++实现）

Binary Search Tree

定义

操作

构造

查找

删除

测试代码

公告