选第k小元素：特定分治策略

 

问题

 在一堆数组当中，选出第k小的数组

分析　

 在一般的情况下面，要选择第k小的数组，要先给它进行排序，排序至少需要O（n * logn）的时间复杂度，但是我们可以用分治的思想，相当于快排，给它进行分组，一组一组的进行排序，虽然也是排序，但是时间复杂度可以到达O(n)。

 

 

 

 

 

 

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int a[N];
void merge(int a[],int left,int mid,int right)
{
    int i,k;
    int *tmp = (int *)malloc((right-left+1)*sizeof(int));
    int left1=left;
    int left2=mid;
    int right1=mid+1;
    int right2=right;
    for(k=0;left1<=left2 && right1<=right2;k++)
    {
        if(a[left1]<=a[right1])
        {
            tmp[k]=a[left1++];
        }
        else
        {
            tmp[k]=a[right1++];
        }
    }
    if(left1<=left2)
    {
        for(i=left1;i<=left2;i++)
        {
            tmp[k++]=a[i];
        }
    }
    if(right1<=right2)
    {
        for(i=right1;i<=right2;i++)
        {
            tmp[k++] = a[i];
        }
    }
    for(i=0;i<right-left+1;i++)
    {
        a[left+i]=tmp[i];
    }
    free(tmp);
    return;
}
void merge_sort(int a[],int left,int right)
{
    int mid = 0;
    if(left<right)
    {
        mid = (left+right)/2;
        merge_sort(a,left,mid);
        merge_sort(a,mid+1,right);
        merge(a,left,mid,right);
    }
    return;
}
int select(int a[],int left,int right,int k) 
{
    int n=right-left;
    if (n<5)
    {
        merge_sort(a,left,right-1);
        return a[left+k-1];
    }
    int i;
    int s=n/5;
    int *m = new int[s];
    for (i=0;i<s;i++) 
    {
        merge_sort(a,left+i*5,left+i*5+5-1);
        m[i] = a[left+i*5+2];
    }
    merge_sort(m,0,i-1);
    int mid=m[i/2];
    int *a1=new int[n];
    int *a2=new int[n];
    int *a3=new int[n];
    int num1=0,num2=0,num3=0;
    for(int i=left;i<right;i++)
    {
        if(a[i]<mid)
        {
            a1[num1++]=a[i];
        }
        else if(a[i]==mid)
        {
            a2[num2++]=a[i];
        }
        else
            a3[num3++]=a[i];
    }
    if(num1>=k)
    {
        return select(a1,0,num1,k);
    }
    if (num1+num2>=k)
    {
        return mid;
    }
    else
        return select(a3,0,num3,k-num1-num2);
}
 
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
    }
    int k;
    scanf("%d",&k);
    printf("%d\n", select(a,0,n,k));
    return 0;
}

 

 时间复杂度

 

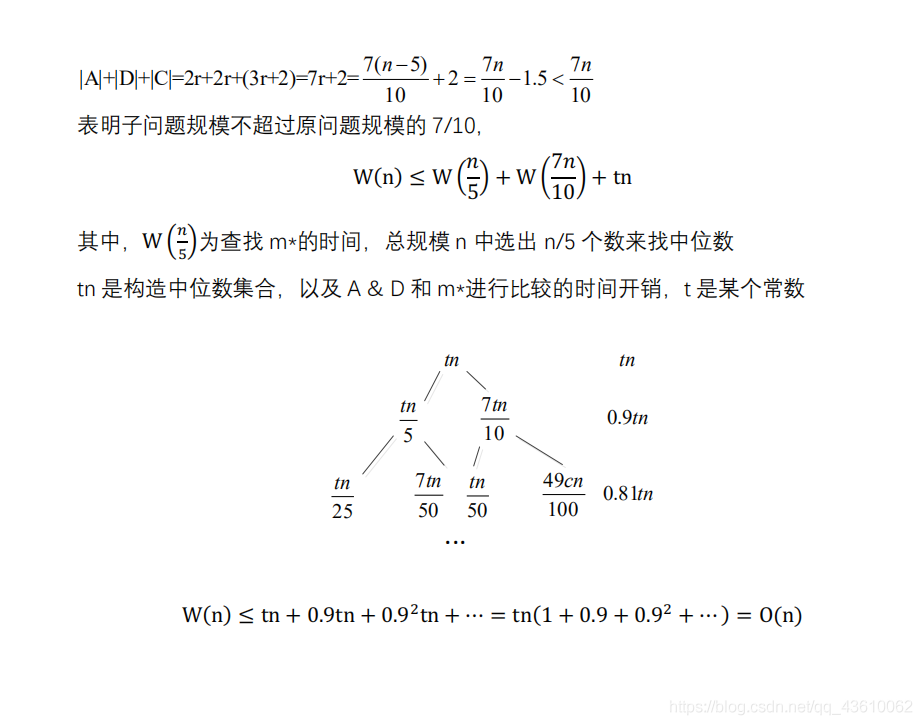
 代码维护

kitalekita/选第k小元素.cpp at main · kitalekita/kitalekita (github.com)