最小生成树 (Prim 与 Kruskal)

概念（问题）

　　在一张有边权的无向图G=（ V , E ）, n = | V | , m = | E | 。 由 V 中全部 n 个顶点和 E 中 n - 1 条边构成的无向连通子图被称为G的一颗生成树。其中边权之和最小的生成树就是此图的最小生成树，一张图的最小生成树不止一颗。那如何去求呢？最小生成树可以用 Prim 和 Kruskal 算法得出。

Prim算法

　　Prim算法是通过点来得出一张无向联通带边权图的最小生成树的。具体步骤是:先选择一个起始点,给它做上标记，然后去寻找与这点相连的路径最小的点，给它也打上标记。接下去去寻找与标记点路径最小的点，如果打上了标记，就去寻找次小的。一直寻找到所有的点都打上了标记。 

　　下面是prim算法的具体步骤用图来表示：

　　

 

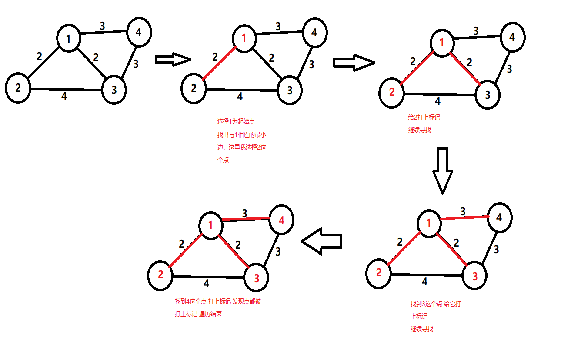
 我们可以清楚的知道这张图的生成树最小权值之和为7。

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<cmath>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 10;
const int inf = 0x3f3f3f3f;
struct edge {
    int v, w, next;
}e[maxn<<1];
int head[maxn], dis[maxn], cnt, n, m, tot, now = 1,ans;
bool vis[maxn];
void add(int u, int v, int w) {
    e[++cnt].v = v;
    e[cnt].w = w;
    e[cnt].next = head[u];
    head[u] = cnt;
}
int prim() {
    for (int i = 2;i <= n;i++) {
        dis[i] = inf;
    }
    for (int i = head[1];i;i = e[i].next) {
        dis[e[i].v] = min(dis[e[i].v], e[i].w);
    }
    while (++tot < n) {
        int minn = inf;
        vis[now] = 1;
        for (int i = 1;i <= n;i++) {
            if (!vis[i] && minn > dis[i]) {
                minn = dis[i];
                now = i;
            }
        }
        ans += minn;
        for (int i = head[now];i;i = e[i].next) {
            int v = e[i].v;
            if (dis[v] > e[i].w && !vis[v]) {
                dis[v] = e[i].w;
            }
        }
    }
    return ans;
}
void run() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v, w;i <= m;i++) {
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w);add(v, u, w);
    }
    printf("%d\n", prim());
}
int main() {
    run();
    return 0;
}

kruskal算法

　　kruskal算法是通过边来判断，先将图上的边进行排序，从最小的开始选择，进行插入。如果我所选择的边插入进去，与我以前选择的边构成环，则这条边不要，继续向下找，直到所有的边都被找完。

　　下面是Kruskal算法的具体步骤用图来表示：

 　　

 

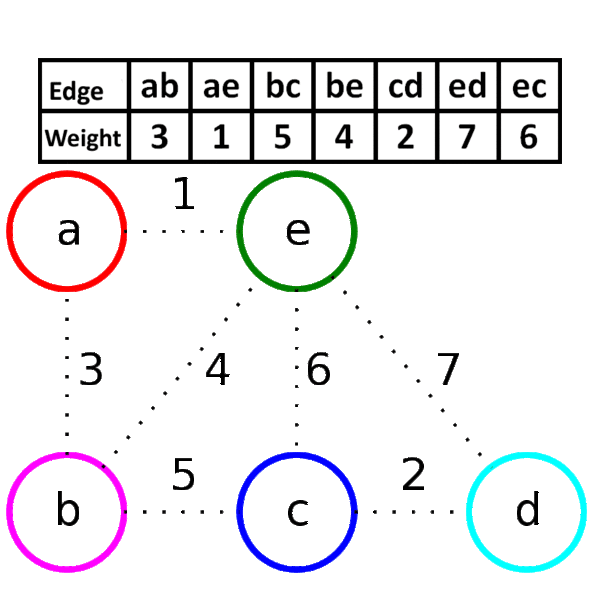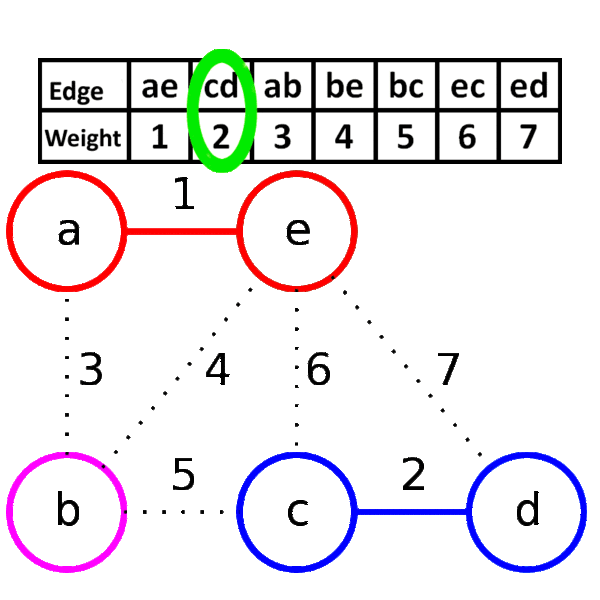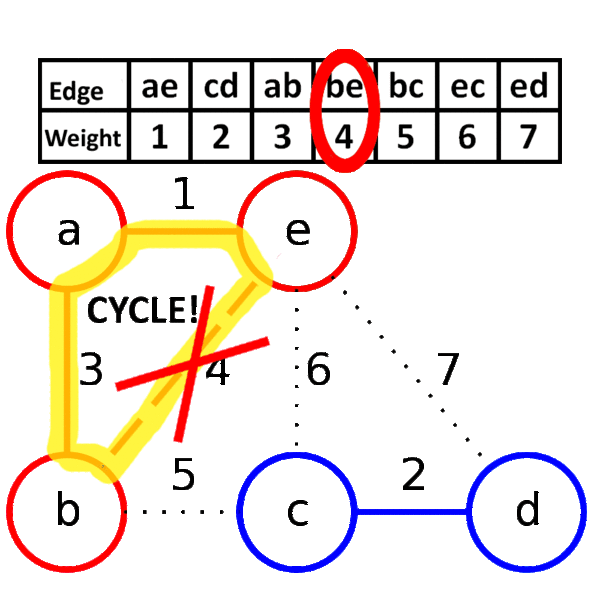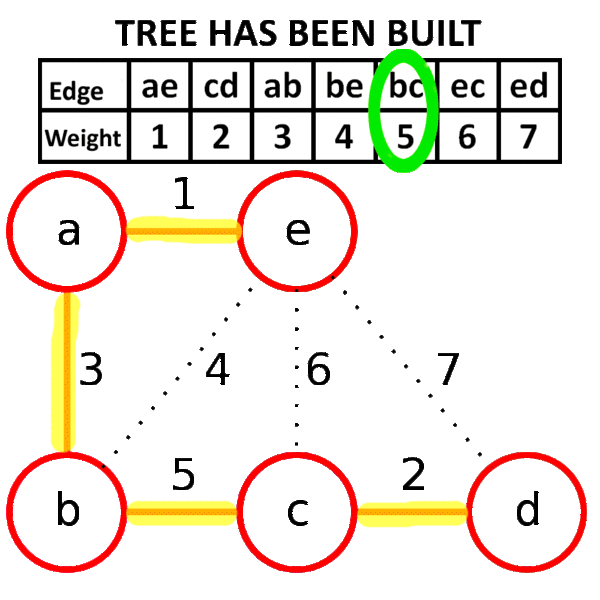
 我们可以清楚的知道这张图的生成树最小权值之和为11。

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 10;
struct edge {
    int u, v, w;
    bool friend operator<(const edge& a, const edge& b) {
        return a.w < b.w;
    }
}e[maxn];
int fa[maxn], n, m, ans, eu, ev, cnt;
int find(int x) {
    return x == fa[x] ? x: fa[x] = find(fa[x]);
}
void kruskal() {
    sort(e + 1, e + 1 + m);
    for (int i = 1;i <= m;i++) {
        eu = find(e[i].u), ev = find(e[i].v);
        if (eu == ev) {
            continue;
        }
        ans += e[i].w;
        fa[ev] = eu;
        if (++cnt == n - 1) {
            break;
        }
    }
}
void run() {
    scanf("%d%d", &n, &m);
    for (int i = 1;i <= n;i++) {
        fa[i] = i;
    }
    for (int i = 1;i <= m;i++) {
        scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
    }
    kruskal();
    printf("%d\n", ans);
}
int main() {
    run();
    return 0;
}

 

分析

　　prim 和 kruskal 算法 由于它们所通过的方法不一样，所以对不同图的处理速度是不一样的。prim是通过点来推的，所以prim 适合点较小的图，而点较多的图一般处理起来会比较慢，时间复杂度为O（V²）。而kruskal算法适用于稀疏图，而稠密图运算起来比较慢，时间复杂度为O(ElogE).

源代码：

https://github.com/kitalekita/kitalekita/blob/main/kruskal.cpp

https://github.com/kitalekita/kitalekita/blob/main/prim.cpp