牛顿法、拟牛顿法、阻尼牛顿法、修正牛顿法

牛顿法的思想是利用目标函数的二次Taylor展开模型的极小点去逼近目标函数的极小点。

设f(x)二次连续可微，Hesse矩阵正定，在x_k附近展开f

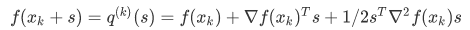
令等式取0，得牛顿迭代公式

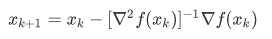，即

 

 

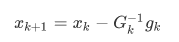
 当初始点距离最优解较远时，G_k不一定正定，迭代不一定收敛，因此引入了步长因子α

带步长因子的牛顿法，即阻尼牛顿法，迭代格式如下：

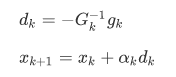
其中α由线性搜索得到。

 

 

牛顿法的关键是计算Hesse矩阵，但对于一般的函数Hesse矩阵不容易计算，为克服这个缺陷，提出了拟牛顿法和修正牛顿法

修正牛顿法的思想是用G+μI来代替G，因为只要μ充分大，就能保证G+μI正定

 

拟牛顿法与牛顿法的区别在于用Hesse矩阵的近似B来代替G，其中B是对称正定的

拟牛顿法的一般步骤如下：

其中拟牛顿条件为

 

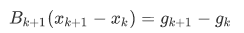
 关于B_k的校正有两种方法——DFP校正和BFGS校正

DFP校正公式为

 

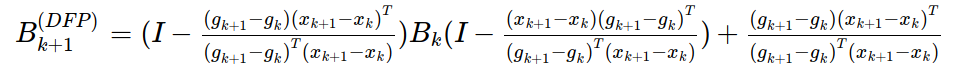
BFGS校正公式为

 

 

 

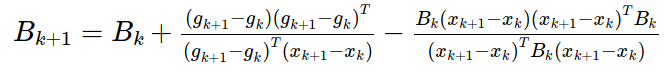
下面给出这几种方法的python实现

阻尼牛顿法：

from linear_search.wolfe import *
from linear_search.Function import *
from numpy import *


def newton(f, start):
    fun = Function(f)
    x = array(start)
    g = fun.grad(x)
    while fun.norm(x) > 0.01:
        G = fun.hesse(x)
        d = (-dot(linalg.inv(G), g)).tolist()[0]
        alpha = wolfe(f, x, d)
        x = x + alpha * array(d)
        g = fun.grad(x)
    return x

 

拟牛顿法：

# coding=utf-8
from linear_search.wolfe import *
from linear_search.Function import *
from numpy import *


# 拟牛顿法
def simu_newton(f, start):
    n=size(start)
    fun = Function(f)
    x = array(start)
    g = fun.grad(x)
    B=eye(n)
    while fun.norm(x) > 0.01:
        d = (-dot(linalg.inv(B), g)).tolist()
        alpha = wolfe(f, x, d)
        x_d=array([alpha * array(d)])
        x = x + alpha * array(d)
        g_d=array([fun.grad(x)-g])
        g = fun.grad(x)
        B_d=dot(B,x_d.T)
        B=B+dot(g_d.T,g_d)/dot(g_d,x_d.T)-dot(B_d,B_d.T)/dot(x_d,B_d)
    return x