DS博客作业06—图
1.本周学习总结
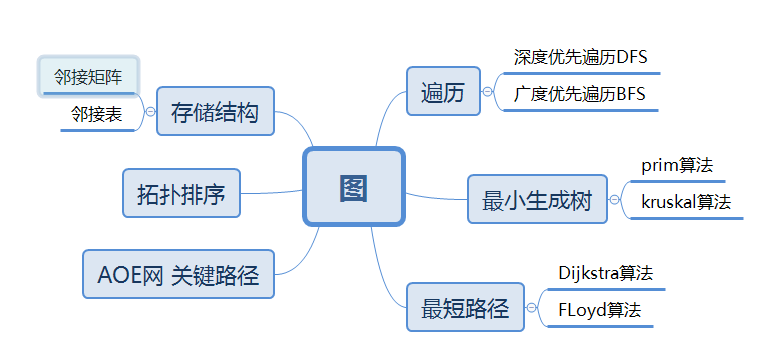
1.1思维导图
1.2学习体会
2.PTA实验作业
2.1 图着色问题
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
2.1.1 设计思路
for i=0 to e
输入邻接表新节点
for i=0 to n
定义set类col存储颜色解种类
for j=1 to v
输入颜色存于数组color中
将该颜色存入col中
if check(v)==true 且 col.size()==k //利用set无视相同元素的特点
输出yes
else
输出no
bool check(int v)
for i=1 to v
for j=0 to G[i].size()
遍历邻接表比较与相邻颜色是否相同
return false //颜色相同
return true
2.1.2 代码截图
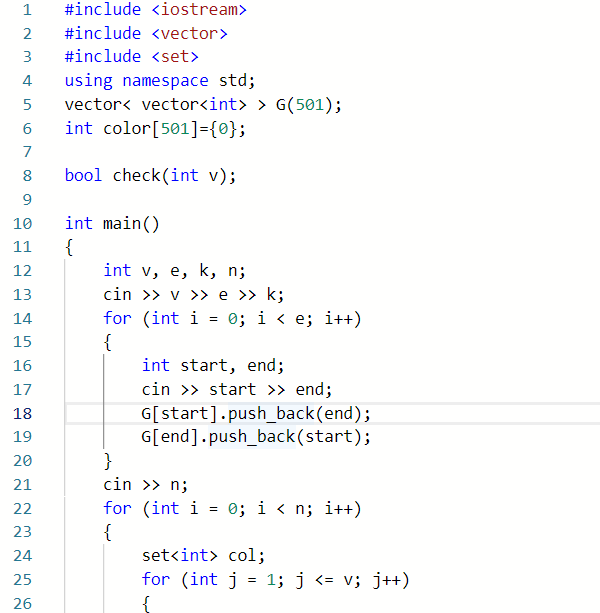

2.1.3 本题PTA提交列表说明

本题尝试使用vector<vector
>方式创建邻接表,大幅压缩代码量
利用set类进行颜色种类计数
2.2 旅游规划
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
2.2.1 设计思路
2.2.2 代码截图
2.2.3 本题PTA提交列表说明
2.3 公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
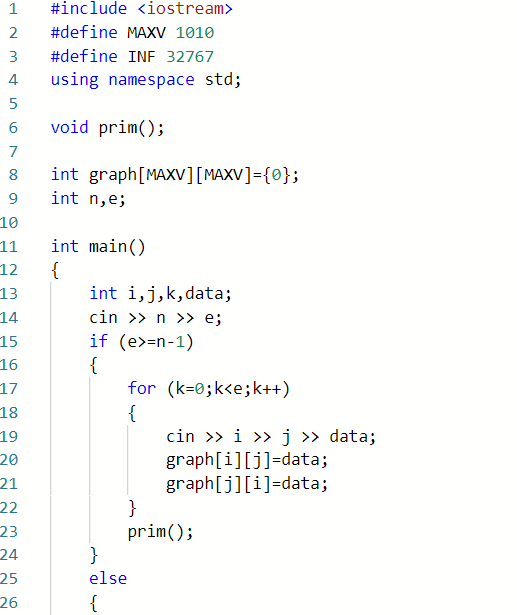
2.3.1 设计思路
输入n,e
if e>=n-1
for k=0 to e
输入顶点 权值
权值存入邻接矩阵
调用prim函数
else //一定不连通
输出-1
定义数组lowcost
for i=1 to n
lowcost赋初值
for i=0 to n
min=INF
for j=1 to n
if lowcost[j] 且 lowcost[j]<=min
min=lowcost[j];
k=j;
lowcost[k]=0
if min!=INF
count+1
cost+=min
for j=1 to n
修正lowcost数组
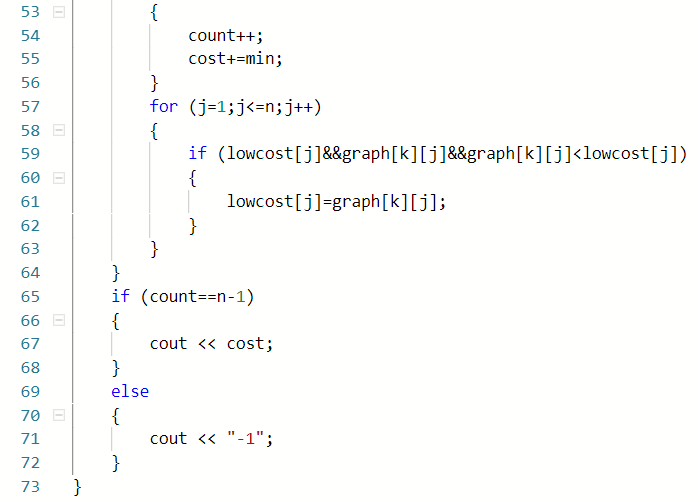
if count==n-1
输出cost
else //不连通
输出-1
2.3.2 代码截图

2.3.3 本题PTA提交列表说明
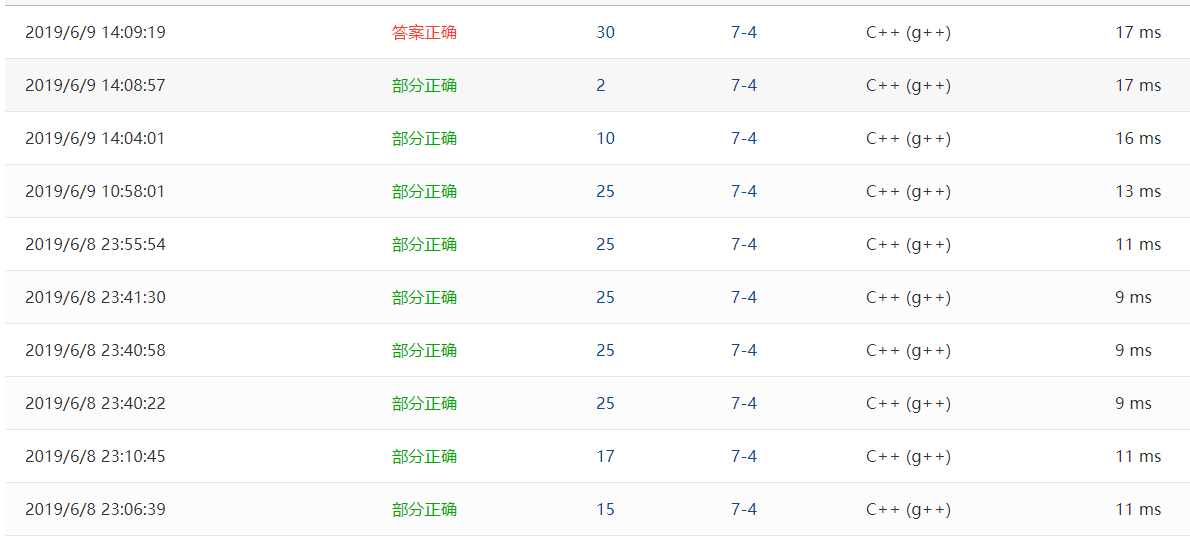
Q1:count判定错误,所有非连通无法显示-1
A1:修正为count==n-1
Q2:M<N-1时段错误
A2:主函数中加入对该情况的判定
Q3:最大M,N答案错误
A3:找了好久直到写算法分析时发现lowcost数组初始化的问题
3.上机考试错题及处理办法
3.1 六度空间
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
3.1.1
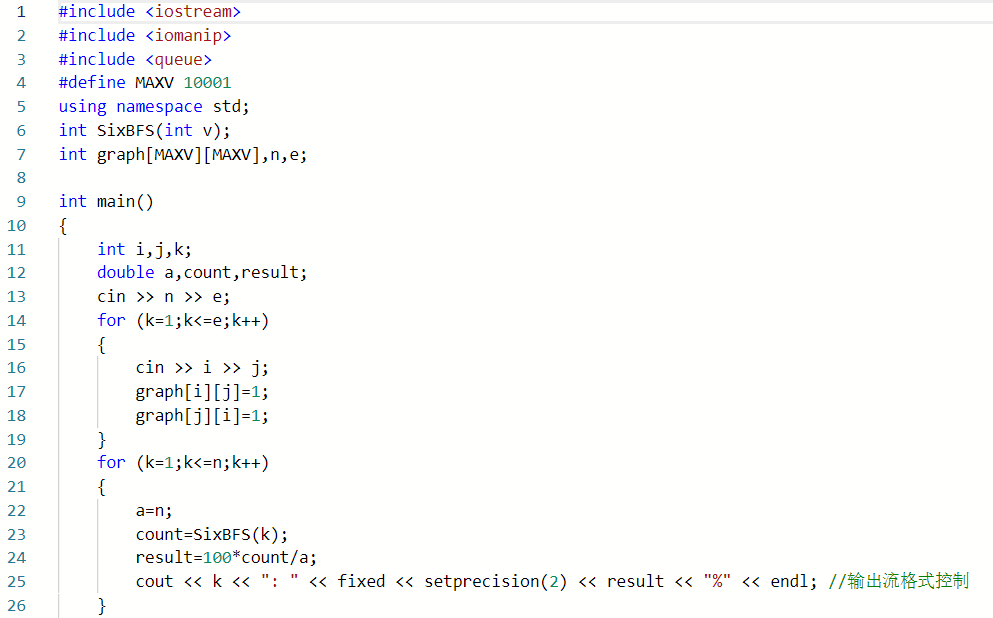
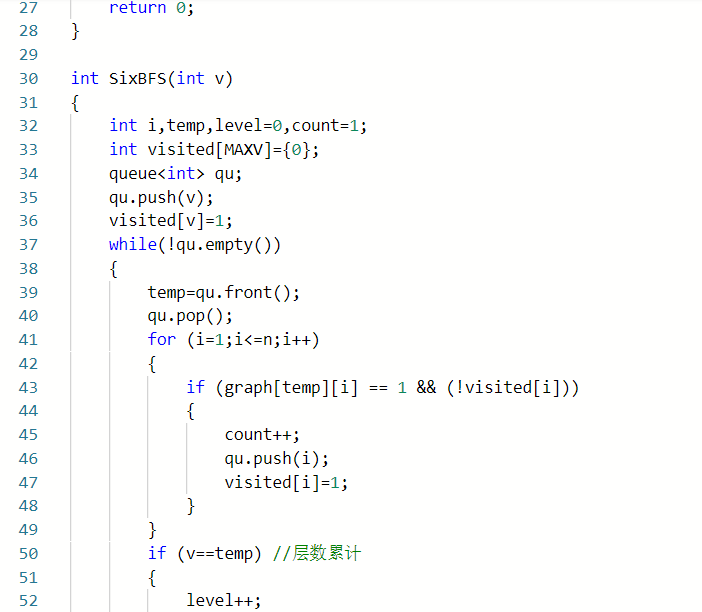

3.1.2
考试时侯的prim算法部分队尾用了qu.front()然后一直debug到收卷
3.2 公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
3.2.1
见2.3.2
3.2.2
直接在邻接矩阵中使用权值,初始化lowcost数组时不能使用课本的方法




