CSP-S模拟11[回文, 快速排序, 混乱邪恶, 校门外歪脖树上的鸽子]

T1 回文

显然，这玩意和传纸条长得贼像,然后对于我赛时调了$1$个多小时的$n ^ {2}$做法感到抱歉....~~我tnm竟然想优化复杂度?~~

看到数据范围,显然可以发现$n ^ {4}$过不了,所以我们传纸条的做法会假，考虑优化
因为是回文,所以我们让两边同时走$(1, 1)$ 和 $(n, m)$一个向下向右走,一个向左向上走,那么显然两边走的路径长度是相等的($i + j - 1$ (起点重复了一次,减掉)),既然这样我们的第四维显然没用了,可以通过前三维求出。
所以我们定义$dp$柿子为$dp_{i, j, k}$表示我从$(1, 1)$走到$(i, j)$,另一边走到$k$行的方案数
转移应该都能想到,就是下一步的落脚点相同的话就直接转移就行
这里考虑答案怎么统计
我们可以分步数的奇偶来处理
- 奇数(n + m - 1)
  
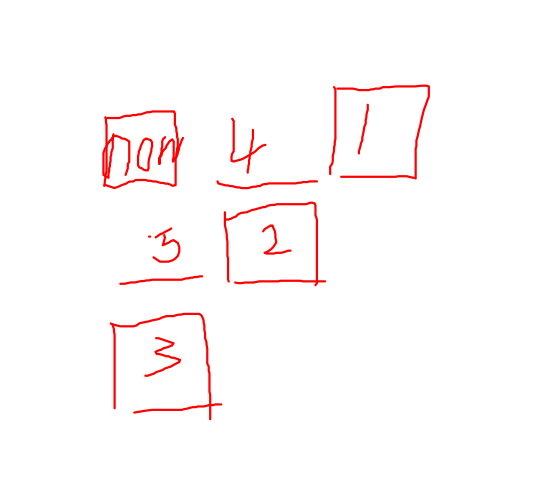
  显然如果我们两边相遇了的话中间会有空档,共有三种情况，$now$和$1$,
  $now$和$2$,$now$和$3$会产生贡献,但是对于$now$和$2$会产生两次贡献(从$4$或者从$5$),所以注意统计时不要遗漏
- 偶数
  显然只有同一行或者同一列的情况，直接统计就行
  -对于另一边$y$的计算，我们可以通过$n + m - i - j - k + 2$这个柿子得出
  对于我们现在已经到了$k$行，所以我们走了$n - k + 1$步，我们总共走了$i + j - 1$步,所以我们还剩下$i + j - n + k - 2$步,那么我们从起点走的步数已经在向上走时算了，所以我们应该用$m - 1$减去上边那坨，就可以得出上柿
当然，这个题还得卡场，大家可以加一下$O(3)或者O(-fast)$之类的东西,以及把取模改成减,把$ans$用$int$存等..
由于我写的太丑，又臭又长，就挂一下$whpan$的了

here



#define HT_walnut no tui,juan
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
#include <iostream>
#include <cstring>
using namespace std;
#define ll long long
inline int in(){
    int x = 0;
    bool f = 0;
    char c = getchar();
    while(c > '9' || c < '0'){
        if(c == '-') f = 1;
        c = getchar();
    }
    while(c <= '9' && c >= '0'){
        x = (x << 3) + (x << 1) + (c ^ 48);
        c = getchar();
    }
    if(f) return -x;
    else return x;
}
const int N = 510;
const int mod = 993244853;
int n,m;
int bh[5] = {0,0,1,0,-1};//右下左上
int bl[5] = {0,1,0,-1,0};
int ans;
int dp[N][N][N];
char s[N][N];
inline void ck(int &x){
    if(x >= mod) x -= mod;
}
int main(){
    // fre(a);
    n = in();
    m = in();
    for(int i = 1;i <= n;++i) scanf("%s",s[i] + 1);
    if(s[1][1] != s[n][m]){
        printf("0");
        return 0;
    }
    dp[1][1][n] = 1;
    int mx = (n + m - 1) / 2;
    int h1,h2,l1,l2;
    for(int i = 1;i <= n;++i)
        for(int j = 1;i + j <= mx + 1;++j)
            for(int k = n;k >= i;--k)
                for(int p = 1;p <= 2;++p)
                    for(int q = 3;q <= 4;++q){
                        h1 = i + bh[p];
                        h2 = k + bh[q];
                        l1 = j + bl[p];
                        if(s[h1][l1] == s[h2][n + m - i - j - k + 2 + bl[q]])
                            dp[h1][l1][h2] += dp[i][j][k],ck(dp[h1][l1][h2]);
                    }
    if((n + m) & 1){
        for(int i = 1;i <= n;++i)
            for(int k = 0;k <= 1;++k)
                ans += dp[i][mx - i + 1][i + k],ck(ans);
    }else{
        for(int i = 1;i <= n;++i){
            for(int k = 0;k <= 2;++k)
               ans += dp[i][mx - i + 1][i + k],ck(ans);
            ans += dp[i][mx - i + 1][i + 1],ck(ans);
        }
    }
    printf("%d",ans);
    return 0;
}

T2 快速排序

~~伪代码比正经代码还好理解的说~~

通过我们观察题目里的代码可以发现他的这个快排在干什么,他在暴力将序列里的所有数和第一个数字比较，大于第一个的放后边，小于的放前边,然后分治,显然$n ^ {2}$，不理解的可以用我下边的代码输出看一下
所以我们就可以优化掉他的过程,当然,对于$nan$这个东西,他是不会更改位置的,即是不会对我排序的结果产生影响,我们只需要扫到它把它插入就行了
我们可以维护一个$multiset$然后从头向后扫,把小于当前数的输出完后,将自己输出就行..真的很简单，我其实还是写麻烦了，大家能不用$STL$尽量不用

here



#include <bits/stdc++.h>
#define LL long long
#define Re register int
#define LD double
#define mes(x, y) memset(x, y, sizeof(x))
#define cpt(x, y) memcpy(x, y, sizeof(x))
#define fuc(x, y) inline x y
#define fr(x, y, z)for(Re x = y; x <= z; x ++)
#define fp(x, y, z)for(Re x = y; x >= z; x --)
#define delfr(x, y, z)for(Re x = y; x < z; x ++)
#define delfp(x, y, z)for(Re x = y; x > z; x --)
#define frein(x) freopen(#x ".in", "r", stdin)
#define freout(x) freopen(#x ".out", "w", stdout)
#define ki putchar('\n')
#define fk putchar(' ')
#define WMX aiaiaiai~~
#define pr(x, y) pair<x, y>
#define mk(x, y) make_pair(x, y)
#define pb(x) push_back(x)
#define re(x) return x
#define sec second
#define fst first
using namespace std;
namespace kiritokazuto{
    auto read = [](){
        LL x = 0;
        int f = 1;
        char c;
        while (!isdigit(c = getchar())){ if (c == '-')f = -1; }
        do{ x = (x << 1) + (x << 3) + (c ^ 48); } while (isdigit(c = getchar()));
        return x * f;
    };
    template  <typename T> fuc(void, write)(T x){
        if (x < 0)putchar('-'), x = -x;
        if (x > 9)write(x / 10); putchar(x % 10 | '0');
    }
}

using namespace kiritokazuto;

const int maxn = 5e5 + 100, Mod = 1e9 + 7;
const LL Inf = 2147483647;

#define int long long

struct num {
    bool isnan;
    int val;
};
// bool operator < (const num& x, const num& y) {
//         if(x.isnan || y.isnan)
//                 return false;
//         return x.val < y.val;
// }
num tmp[1 << 20];
num a[maxn];
int ans[maxn];
int n;
int pos[maxn];
// void qsort(num* _begin, num* _end, int type )
// {
//         // printf("TTT _begin %d   _end %d type = %d\n", _begin -> val, _end -> val, type);
//         if(_begin + 1 >= _end)
//                 return;
//         num aa = *_begin, *s = _begin, *t = tmp;
//         for(num* p = _begin + 1; p < _end; p++)
//         {
//                 if(*p < aa)*s = *p, s++;//小的向前挪
//                 else *t = *p, t++;//大的向后挪
//         }
//         *s = aa, s++;//把所有数字和头比较
//         for(t--; t >= tmp; t--) *(s + (t - tmp)) = *t;

//         // printf("KKK type = %d s = %d\n", type, s -> val);
//     //     fr(i, 1, n) {
//     //        if(a[i].isnan) {
//     //            printf("nan ");
//     //            continue;
//     //        }
//     //        printf("%lld ", a[i].val);
//     //    }
//     //    ki;、
//         qsort(_begin, s - 1, 1);
//         qsort(s, _end, 2);
// }
int t;

//话说这玩意拿它原程序跑不行吗?
int tot;
multiset <pr(int, int)> st;

signed main() {  
   t = read();
   while(t --) {
       n = read();
    //    fr(i, 1, n){
    //     //    pos[i] = 0;
    //        a[i].val = 0;
    //        a[i].isnan = 0;
    //    }
    //    char s[100];
       string s;
       tot = 0;
       st.clear();
       fr(i, 1, n) {
           
           pos[i] = 0;
           cin >> s;
           if(s[0] == 'n') {
               a[i].isnan = 1;
            //    pos[i] = 1;
            //    a[i].val = Inf;
               continue;
           }
            int x = 0;
            delfr(j, 0, s.size()){
                x = (x << 1) + (x << 3) + (s[j] ^ 48) ;
            }
            a[i].isnan = 0;
            a[i].val = x;   
            st.insert(mk(x, i));
       }
       fr(i, 1, n) {
           if(pos[i])continue;
           if(a[i].isnan){ans[++tot] = 114514;continue;}
           while((*st.begin()).fst < a[i].val) {//把小的向前放
               ans[++tot] = (*st.begin()).fst;
               pos[(*st.begin()).sec] = 1;
               st.erase(st.begin());
           }
           ans[++tot] = (*st.begin()).fst;//自己
           pos[(*st.begin()).sec] = 1;
           st.erase(st.begin());
       }
        fr(i, 1, n) {
            if(ans[i] == 114514){
                printf("nan ");
                continue;
            }
            // write(ans[i]), fk;
            printf("%lld ", ans[i]);
        }
        ki;
 
    //    qsort(a + 1, a + n, 0);
    //    fr(i, 1, n) {
    //        if(a[i].isnan) {
    //            printf("nan ");
    //            continue;
    //        }
    //        printf("%lld ", a[i].val);
    //    }
    //    ki;
   }
   re(0);
}

T3 混乱邪恶

万恶的数学题，问了数学奥赛的朋友，他们说这个题当年对数奥是让证明$\frac{2}{3} \times m$是最优秀的下界...~~好像更ex~~

首先放假做法,这能$A$掉我是没想到的,不过需要~~极致的常技巧和评测机对你的青睐~~，我们可以暴搜过,$96pts$是稳的，就是$AC$不一定

here









%:pragma GCC optimize(3)
%:pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
#define LL long long
#define Re register int
#define LD double
#define mes(x, y) memset(x, y, sizeof(x))
#define cpt(x, y) memcpy(x, y, sizeof(x))
#define fuc(x, y) inline x y
#define fr(x, y, z)for(Re x = y; x <= z; x ++)
#define fp(x, y, z)for(Re x = y; x >= z; x --)
#define delfr(x, y, z)for(Re x = y; x < z; x ++)
#define delfp(x, y, z)for(Re x = y; x > z; x --)
#define frein(x) freopen(#x ".in", "r", stdin)
#define freout(x) freopen(#x ".out", "w", stdout)
#define ki putchar('\n')
#define fk putchar(' ')
#define WMX aiaiaiai~~
#define pr(x, y) pair<x, y>
#define mk(x, y) make_pair(x, y)
#define pb(x) push_back(x)
#define re(x) return x
#define sec second
#define fst first

using namespace std;
namespace kiritokazuto{
    auto read = [](){
        LL x = 0;
        int f = 1;
        char c;
        while (!isdigit(c = getchar())){ if (c == '-')f = -1; }
        do{ x = (x << 1) + (x << 3) + (c ^ 48); } while (isdigit(c = getchar()));
        return x * f;
    };
    template  <typename T> fuc(void, write)(T x){
        if (x < 0)putchar('-'), x = -x;
        if (x > 9)write(x / 10); putchar(x % 10 | '0');
    }
}

using namespace kiritokazuto;


const int maxn = 1e6 + 10, maxm = 505;
int n, m;
struct Node {
    int id, val;
    friend bool operator < (Node A, Node B) {return A.val < B.val;}
}a[1000010];
bool is[1000010];
LL sum = 0;
fuc(bool, dfs)(int x){
    
    if (sum == 0) return 1;
    fp(i, x, 1) {
        if(a[i].val > sum)continue;
        sum -= a[i].val;
        
        if(dfs(i - 1)) {
            is[a[i].id] = 1;
            return 1;
        }
        sum += a[i].val;
    }
    return 0;
}
signed main(){
 n = read(), m = read();
    fr(i, 1, n) {
        a[i].val = read();
        a[i].id = i;
        sum += a[i].val;
    }
    sort(a + 1, a + n + 1);
    sum >>= 1;
    int fg = dfs(n);
        printf("NP-Hard solved\n");
        fr(i, 1, n) {
            if(is[i])printf("-1 ");
            else printf("1 ");
        }
 return 0;
}

然后考虑正解的构造，我们最优肯定是排个序，然后相邻的两两消，最后再一起消就好了
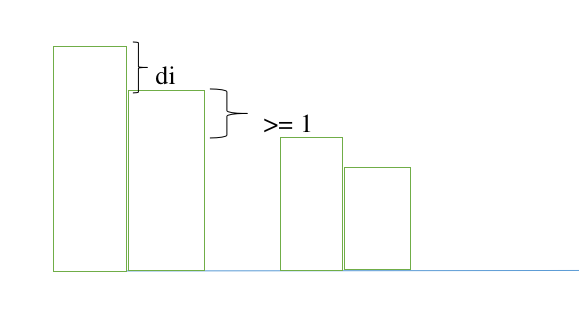
对于题解上$\sum d_{i} \leq m - \frac{n}{2} < n$我们可以画一个图来证明
因为我们是排完序两两配对的,所以相邻的一组之间最少差一，那么我们是一个大小为$m$的子集,所以最大值最大是$m$,我们有$\frac{n}{2}$个组,所以我们$\sum d_{i}$最多也就有$m - \frac{n}{2}$了,剩下的就好证了
其次对于$n = 1$因为一定是偶数,所以$d_{i}$又小于$2 * n$，只能是$0$
对于$n = k$， $d_{i} = 1$的情况,我们显然可以一正一负来做到
当然，在之后消去两个 $d_{i} $产生新的 $d_{i}$ 的过程中,其实没必要只用最大值减去最小值,只要保证减掉的是一个偶数,能让最终消完就行,当然,别减出零来,否则就爆了
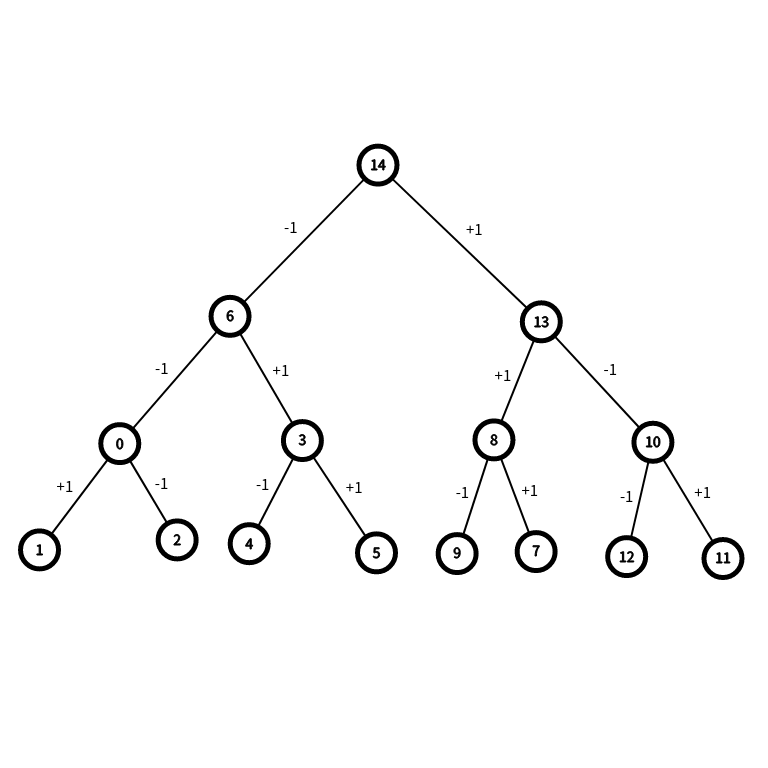
所以最终的解法可以抽象为一颗类似与树的东西
将边权表示成边,这个有两种解法,可以用$dfs$,也可以用$while$暴力
当然在处理的时候注意正负号的改变,比如我要减一个$(big - sml)$,脱了括号之后会变号的,我们可以将他们看成一坨括号，将括号外的符号传递进去，再去处理括号里的
具体怎么进行,我们可以用$multiset$维护一个结构体,记录$d_{i}$以及它的来源,然后一直向上传就行,在维护$d_{i}$的时候注意边界有两个$size == 1$以及全是$1$
然后在传递的时候记得那个标记应该打到谁身上,我这里的$1$ ~ $\frac{n}{2}$是原来的数组直接做差得到的$d_{i}$,而$\frac{n}{2}$之后的是$d_{i}$之间做差得到的新的$d_{i}$，所以注意标记打的位置,新的打在结构体里，原来的直接打在原数组上

multiset



#include <bits/stdc++.h>
#define LL long long
#define Re register int
#define LD double
#define mes(x, y) memset(x, y, sizeof(x))
#define cpt(x, y) memcpy(x, y, sizeof(x))
#define fuc(x, y) inline x y
#define fr(x, y, z)for(Re x = y; x <= z; x ++)
#define fp(x, y, z)for(Re x = y; x >= z; x --)
#define delfr(x, y, z)for(Re x = y; x < z; x ++)
#define delfp(x, y, z)for(Re x = y; x > z; x --)
#define frein(x) freopen(#x ".in", "r", stdin)
#define freout(x) freopen(#x ".out", "w", stdout)
#define ki putchar('\n')
#define fk putchar(' ')
#define WMX aiaiaiai~~
#define pr(x, y) pair<x, y>
#define mk(x, y) make_pair(x, y)
#define pb(x) push_back(x)
#define re(x) return x
#define sec second
#define fst first


using namespace std;
namespace kiritokazuto{
    auto read = [](){
        LL x = 0;
        int f = 1;
        char c;
        while (!isdigit(c = getchar())){ if (c == '-')f = -1; }
        do{ x = (x << 1) + (x << 3) + (c ^ 48); } while (isdigit(c = getchar()));
        return x * f;
    };
    template  <typename T> fuc(void, write)(T x){
        if (x < 0)putchar('-'), x = -x;
        if (x > 9)write(x / 10); putchar(x % 10 | '0');
    }
}

using namespace kiritokazuto;
const int maxn = 1e6 + 10;
struct Node {
    int big, sml;
    int id;
    int val;
    int is;
    friend bool operator < (Node A, Node B){
        return A.val < B.val;
    }
}tp[maxn];
int l = 1, r = 0;
int num;
int n, m, tmp;
int a[maxn], b[maxn];
LL sum;
int is[maxn];
int tong[maxn];
multiset <Node> s;
int rp;
signed main() {
    tmp = n = read();
    m = read();
    fr(i, 1, n) {
        b[i] = a[i] = read();
    }
    if(n & 1)a[++n] = 0;
    sort(a + 1, a + n + 1);
    for(Re i = 1; i <= n - 1; i += 2) {
        int res = a[i + 1] - a[i];
        int pos = i / 2 + 1;
        tp[++num].val = res;
        tp[num].big = a[i + 1];
        tp[num].sml = a[i];
        tp[num].id = pos;
        sum += res;
        s.insert(tp[num]);
    }
    if(sum & 1 || sum >= n){
        printf("Chaotic evil");
        re(0);
    }
    printf("NP-Hard solved\n");
    n /= 2;
    num = n;
    while(1) {
        auto Max = --s.end();
        auto Min = s.begin();
        if(s.size() == 1) {
            tong[++r] = (*Max).id;
            break;
        }
        if((*Max).val == 1) 
        {
            bool iss = 0;
            for(auto it = s.begin(); it != s.end(); it ++) {
                if(iss)tp[(*it).id].is = 1;
                tong[++r] = (*it).id;
                iss ^= 1;
            }
            break;
        }
        tp[++num].id = num;
        tp[num].val = tp[(*Max).id].val - tp[(*Min).id].val;
        tp[num].big = (*Max).id;
        tp[num].sml = (*Min).id;
        s.erase(Max);
        s.erase(Min);
        s.insert(tp[num]);
    }
    while(l <= r) {
        int now = tong[l++];
        if(now <= n){//n / 2
            if(tp[now].is)is[tp[now].big] = 1;
            else is[tp[now].sml] = 1; 
        }else {
            tong[++r] = tp[now].big;
            tong[++r] = tp[now].sml;
            if(tp[now].is)tp[tp[now].big].is = 1;
            else tp[tp[now].sml].is = 1; 
        }
    }
    fr(i, 1, tmp){
        if(is[b[i]])printf("-1 ");
        else printf("1 ");
    }
    re(0);
}

dfs



#define sandom signed
#define fre(x, y) freopen(#x ".in", "r", stdin), freopen(#y ".out", "w", stdout);
#include <bits/stdc++.h>
#define re register int
using namespace std; int wrt[20], TP;
const int Z = 5e6 + 10;
inline int read() { int x = 0, f = 0; char c = getchar(); while (!isdigit(c)) f = c == '-', c = getchar(); while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar(); return f ? -x : x; }
inline void write(int x) { TP = 0; if (x < 0) putchar('-'), x = -x; while (x >= 10) wrt[++TP] = x % 10, x /= 10; wrt[++TP] = x; while (TP) putchar(wrt[TP--] | 48); putchar(' '); }

int n, m, k, ans;
int a[Z], c[Z], p[Z];
struct moj
{
    int id, val;
    pair <int, int> frm;
    friend bool operator <(moj A, moj B) { return A.val < B.val; }
}; moj nod[Z];
multiset <moj> s;
void solve(int n)
{
    if (n == 1) return;//边界条件，此时和一定为0
    auto t1 = s.begin(), t2 = --s.end();
    moj Min = *t1, Max = *t2;//把最大值与最小值做差
    s.erase(t1), s.erase(t2);
    nod[m] = {m, Max.val - Min.val, make_pair(Max.id, Min.id)};
    s.insert(nod[m++]);//新条件
    solve(n - 1);//继续递归
}
void dfs(int rt, int num)
{
    if (nod[rt].frm.first <= n)//到底了，给出答案
    {
        c[nod[rt].frm.first] = num ? -1 : 1;
        c[nod[rt].frm.second] = num ? 1 : -1;
        return;
    }
    dfs(nod[rt].frm.first, num);
    dfs(nod[rt].frm.second, num ^ 1);//因为做了减法，需要取反
}

sandom main()
{
    n = read(), m = read() + 1;
    for (re i = 1; i <= n; i++) a[i] = read();
    if (n & 1) a[++n] = 0;
    for (re i = 1; i <= n; i++) p[a[i]] = i;
    sort(a + 1, a + 1 + n);
    for (re i = 2; i <= n; i += 2)
    {
        nod[m] = {m, a[i] - a[i - 1], make_pair(p[a[i]], p[a[i - 1]])};
        s.insert(nod[m++]);
    }
    solve(n / 2); dfs(m - 1, 0);
    puts("NP-Hard solved");
    if (a[1] == 0) for (re i = 1; i < n; i++) write(c[i]);
    else for (re i = 1; i <= n; i++) write(c[i]);
    return 0;
}

T4 校门外歪脖树上的鸽子

数据结构ex题目,先咕咕

每日一图

posted @ 2022-09-25 20:45 kiritokazuto 阅读(249) 评论(9) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

kiritokazuto

背灯和月就花阴，已是十年踪迹十年心

CSP-S模拟11[回文, 快速排序, 混乱邪恶, 校门外歪脖树上的鸽子]

T1 回文

T2 快速排序

T3 混乱邪恶

T4 校门外歪脖树上的鸽子

公告