暑假集训五[星际旅行, 砍树, 超级树, 求和]
暑假集训5
星际旅行
这个题刚看我觉得很ex,没事思路,就跳了,然后就去欺负\(T4\)了后来别的不会做,然后回来肝它...就肝出来了...对了,注意开\(long long\)
-
首先转化一下题意,我们建无向边不是一下建两条吗,那么如果想让一条无向边只被走一次,那么我们相当于删除掉它两条边的一条,那题意就可以转化为删除两条边之后,我们判断原图是否存在欧拉路(题目走两次的限制就可已相当于把找到的欧拉路反过来走一遍就可以)
-
回到欧拉路,无向图存在(欧啦)欧拉路的充要条件是
- 图是联通的(边联通 -> 边联通和点联通相当于是割点和割边的区别)
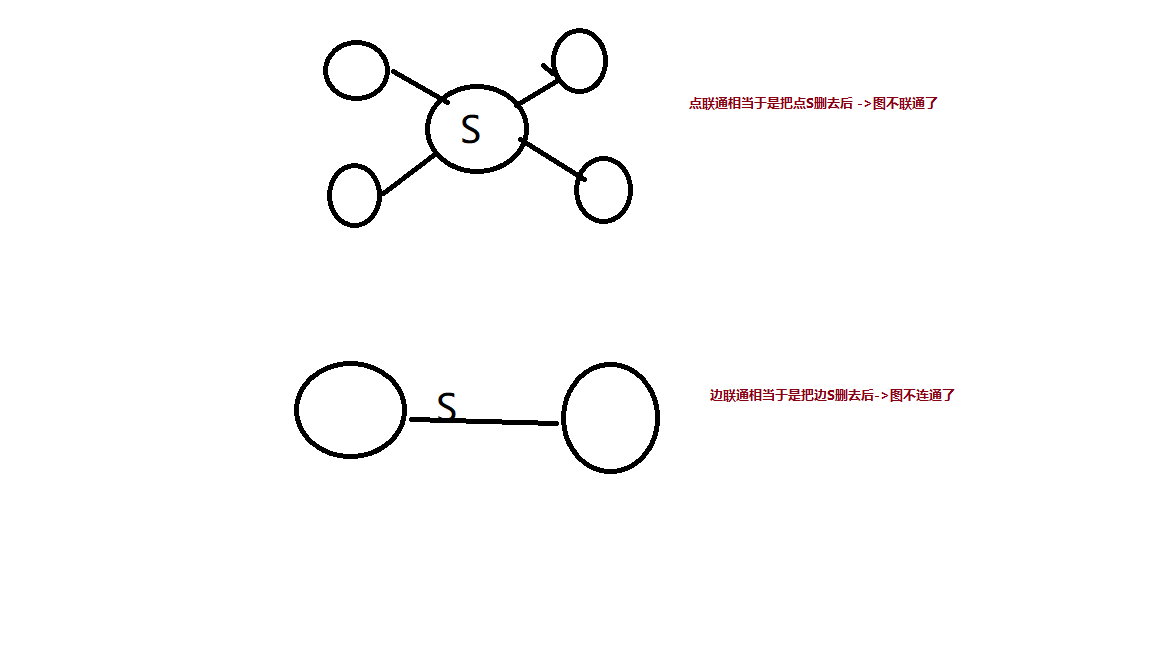
- 只有\(0 / 2\)个点的度数为奇数,如果起点和终点相同则\(0\)个点,不同则一个只有出去,一个只有进来,所以是两个
- 图是联通的(边联通 -> 边联通和点联通相当于是割点和割边的区别)
-
所以现在我们可以考虑删掉什么样的两条边可以使剩下的图可以构成欧拉路
- 首先考虑一个图
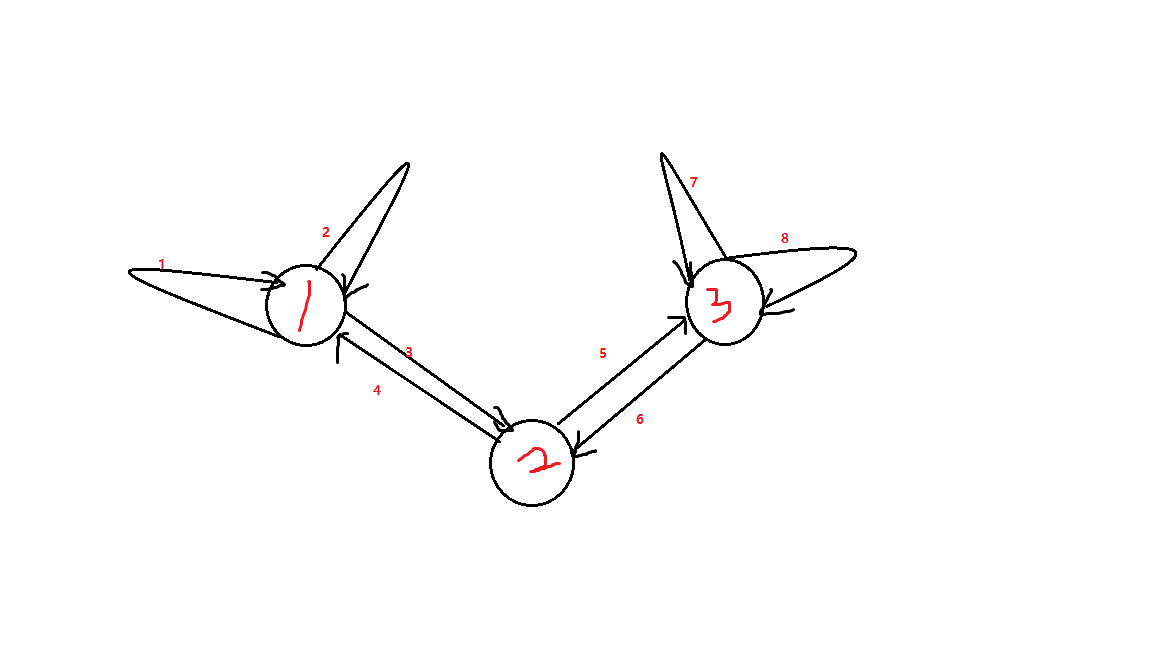
- 这个图的\(ans\)是\(6\),手模可以发现
- 总共只有三种情况合法
- \(1>\) 删除两个自环
- \(2>\) 删除一个自环和一个正常边
- \(3>\) 删除两条有且仅有一个公共顶点的边
- 总共只有三种情况合法
- 考虑正确性
- 对于删除两个个自环,因为自环的度数实际上是可以任意的,既可以当奇又可以当偶,那么我们就可以将那两个点当作奇数度数
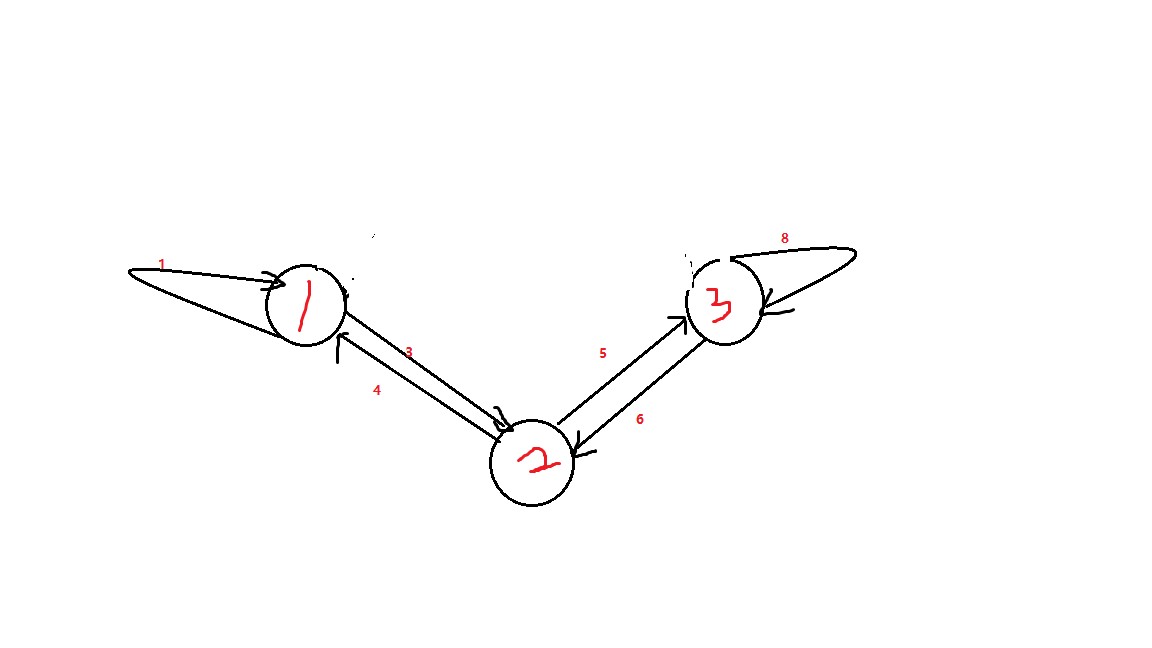 如图删了\(2\)和\(7\)的边,我们可以走$5 -> 8 -> 6 -> 4 -> 1 -> 3 $满足题意
如图删了\(2\)和\(7\)的边,我们可以走$5 -> 8 -> 6 -> 4 -> 1 -> 3 $满足题意 - 对于删除一个自环和一条边,删除自环的一条边对度数没有影响,所以此时那被删去的一条边所相连接的两个顶点的度数一定就是奇数了(原图的度数都是偶数,因为无向边,每连一次边就会加一个入度和出度)
 如图删了\(2\)和\(4\)的边,我们可以走$5 -> 7 -> 8 -> 6 -> 3 -> 1 $满足题意
如图删了\(2\)和\(4\)的边,我们可以走$5 -> 7 -> 8 -> 6 -> 3 -> 1 $满足题意
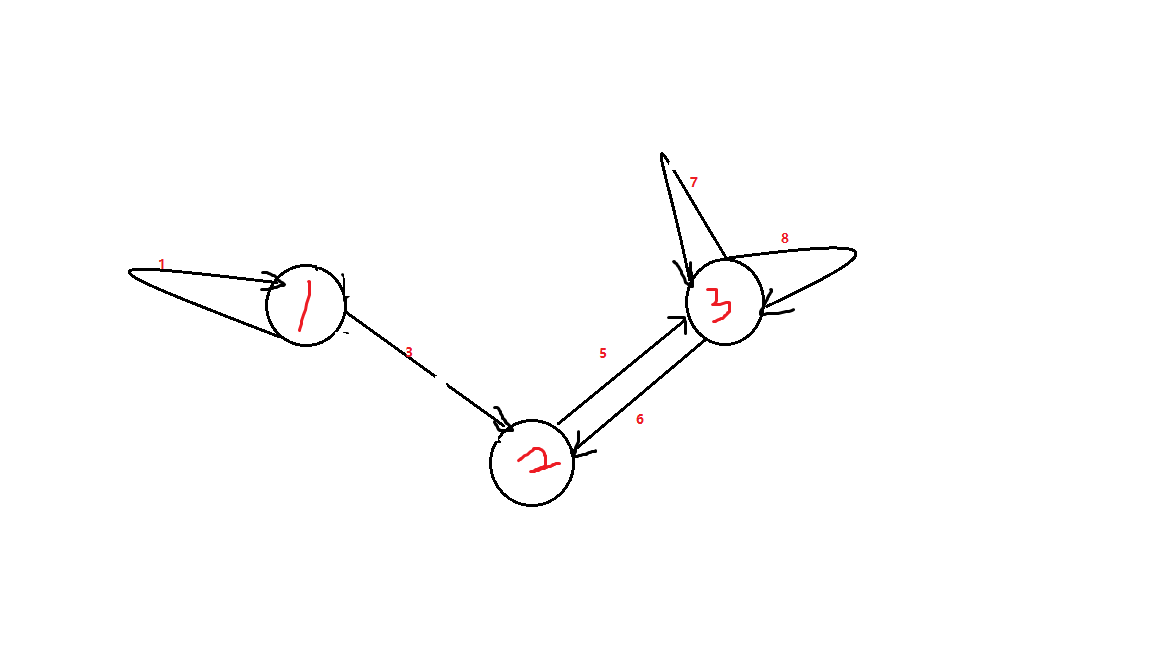
-对于删除两条有且仅有一个公共顶点的边,因为我们删除一个边,就会让所相连接的两个顶点的度数变成奇数,那么如果没有公共顶点的话,\(4\)个奇数点是无法构成欧拉路的,所以有一个公共点能让一个奇数点变回偶数点
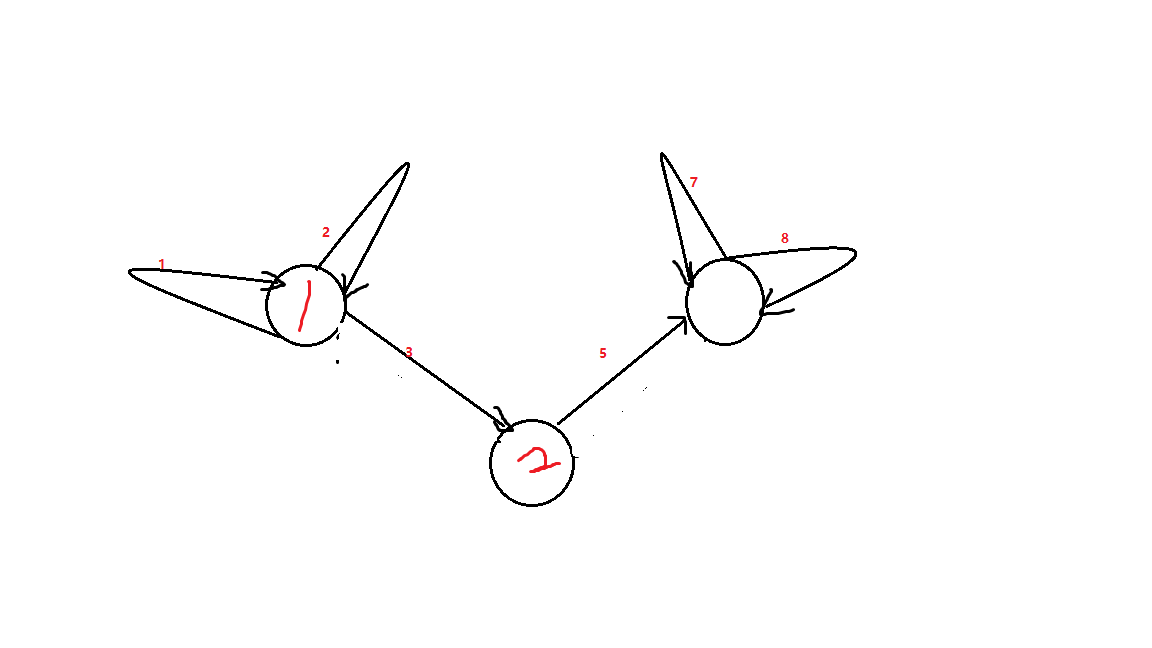 如图删了\(4\)和\(6\)的边,我们可以走$1 -> 2 -> 3 -> 5 -> 7 -> 8 $满足题意
如图删了\(4\)和\(6\)的边,我们可以走$1 -> 2 -> 3 -> 5 -> 7 -> 8 $满足题意
- 对于删除两个个自环,因为自环的度数实际上是可以任意的,既可以当奇又可以当偶,那么我们就可以将那两个点当作奇数度数
- 首先考虑一个图
here
#include <bits/stdc++.h>
#define LL long long
#define Re register int
#define LD long double
#define mes(x, y) memset(x, y, sizeof(x))
#define cpt(x, y) memcpy(x, y, sizeof(x))
#define fuc(x, y) inline x y
#define fr(x, y, z)for(Re x = y; x <= z; x ++)
#define fp(x, y, z)for(Re x = y; x >= z; x --)
#define frein(x) freopen(#x ".in", "r", stdin)
#define freout(x) freopen(#x ".out", "w", stdout)
#define ki putchar('\n')
#define fk putchar(' ')
#define WMX aiaiaiai~~
#define pr pair<long long, long long>
#define mk(x, y) make_posair(x, y)
using namespace std;
namespace kiritokazuto{
auto read = [](){
LL x = 0;
int f = 1;
char c;
while (!isdigit(c = getchar())){ if (c == '-')f = -1; }
do{ x = (x << 1) + (x << 3) + (c ^ 48); } while (isdigit(c = getchar()));
return x * f;
};
template <typename T> fuc(void, write)(T x){
if (x < 0)putchar('-'), x = -x;
if (x > 9)write(x / 10); putchar(x % 10 | '0');
}
}
using namespace kiritokazuto;
const int maxn = 1e5 + 10, Mod = 1e9 + 7;
const int Inf = 2147483647;
//无向图
//有自环
//话说这玩意真的不是排列组合吗?
//(23 24 25 34 35 45 。。。。。)
/*
本质不同
1> 起点不同
2> 终点不同
3> 走不同性质的边(点)
4> 当且仅当至少存在一个虫
洞,在两条航线中经过的次数不同
*/
/*
我行过许多地方的桥,看过许多次数的云,喝过许多不同种类的酒
却只爱过一个正当最好年纪的人
*/
//它相当于是让我走完,应该是一笔画
//话说昨天long long卡我那么多,今天全开long long 妈的
bool vis[maxn];
LL ans = 0;
LL deg[maxn];
int n;
int m;
struct Node{
int to, next;
}wmx[maxn << 1];
int head[maxn], len = 0;
fuc(void, Qian)(int from, int to){
wmx[++len].to = to;
wmx[len].next = head[from];
head[from] = len;
}
int cir, cnt;
//cir为自环的个数, cnt为正常边的个数
//又想暴力删边了
/*
!!!!
被删去的两条边一定连在同一个顶点上
否则删了他们之后就会有 4个度数为奇数的点
跑不了一笔画
连在一起则4 - 2 = 2还是偶数
然后我分情况讨论
1> 删两个自环
2> 删一个自环和一个边(不用在一个顶点上)
3> 删在同一个顶点上的两条边
*/
fuc(void, dfs_check)(int x){
vis[x] = 1;
for (Re i = head[x]; i; i = wmx[i].next){
int to = wmx[i].to;
if (!vis[to])dfs_check(to);
}
}
signed main(){
n = read();
m = read();
fr(i, 1, m){
int x = read(), y = read();
if (x == y){ cir++; continue; }//自环的deg不计入,不连边
deg[x] ++;
deg[y] ++;
Qian(x, y);
Qian(y, x);
}
cnt = m - cir;
if (cir == m){
printf("0");
return 0;
//全是自环啥也不行,图不联通
}
fr(i, 1, n){
if (deg[i]){ dfs_check(i); break; }
}//判断联通否
fr(i, 1, n){
if (deg[i] && !(vis[i])){//图不联通
printf("0\n");
return 0;
}
}
fr(i, 1, n)ans += (deg[i] * (deg[i] - 1)) >> 1;//第三种
ans += (cir * (cir - 1)) >> 1;//随便删两个自环,删完之后那两个点就成deg为奇的;了
ans += cnt * cir;//两个组合
write(ans);
return 0;
}
/*
5 4
1 2
1 3
1 4
1 5
3 4
1 1
2 1
2 3
3 3
*/
砍树
这个题没有单调性,不能二分,呜呜呜
-
这个题目等价于求出一个最大的\(d\)
满足\(\large \sum\limits_{i = 1}^{n}(\left \lceil \frac{a_i}{d} \right \rceil * d - a_i)\leq k\)
(为啥向上取整很显然把,我得等他长够啊) -
所以我设\(\large C = k + \sum\limits_{i = 1} ^ {n}a[i]\)
-
那么显然\(\large \sum\limits_{i = 1} ^ {n}\left \lceil \frac{a_i}{d} \right \rceil * d \leq c\)
-
那么根据数论分块就可以很简单的去做了,另外对于一个块内的值都是一样的,所以不会有遗漏
-
数论分块在这里就证明一个东西,他的边界
$ \begin{aligned}
&\frac{a}{b}=\left\lfloor\frac{a}{b}\right\rfloor+r(0\leq r<1)\
\implies
&\left\lfloor\frac{a}{bc}\right\rfloor
=\left\lfloor\frac{a}{b}\cdot\frac{1}{c}\right\rfloor
=\left\lfloor \frac{1}{c}\left(\left\lfloor\frac{a}{b}\right\rfloor+r\right)\right\rfloor
=\left\lfloor \frac{\left\lfloor\frac{a}{b}\right\rfloor}{c} +\frac{r}{c}\right\rfloor
=\left\lfloor \frac{\left\lfloor\frac{a}{b}\right\rfloor}{c}\right\rfloor\
&&\square
\end{aligned} $
- 此外,对于代码中的一些操作做出解释,\(C / (C / l)\)最外端的\(floor\)可加可不加,因为整数运算本来就是向\(0\)取整,在这里是可以当作向下取整的,对于\(ceil(1.0 * a_i / x)\)是因为如果先让\(a_i/x\)之后直接去\(ceil\)会丢失精度,已经向\(0\)取整了,再向上取整没有意义,所以用 浮点数保留精度
fuc(bool, check)(int x){
int res = 0;
fr(i, 1, n){
res += ceil(1.0 * Exp[i] / x);
}
return res * x <= C;
}
signed main(){
n = read();
k = read();
fr(i, 1, n)Exp[i] = read(), C += Exp[i];
C += k;
for (Re l = 1, r; l <= C; l = r + 1){
r = floor(C / (C / l));
if (check(r)){
ans = r;
}
}
write(ans);
return 0;
}
超级树
怎么天天都是神仙dp啊,放过我吧
-
考虑\(sb\)(帅比(雾)\(dp\)的定义
\(dp[i][j]\)表示一颗\(i -\)超级树,有\(j\)条点不重复的路径的方案数,因为我们要通过 \(k\)去更新\(k + 1\)所以我们的层数相当于是倒着的,分成子问题
-
首先初始化\(dp[1][0] = dp[1][1] = 1\),最终的答案为\(dp[k][1]\)注意这里的\(1\)是一段,既可以是单点,也可以是多个等等,有一种子段和的感觉
-
下边考虑转移
-
我们枚举左子树和右子树的路径条数\(l、r\),记\(num = dp[k][l] * dp[k][r]\)乘法原理
-
\(1>\) 第\(k + 1\)层的根什么也不做,即不考虑它单点的贡献,则有
\(\large dp[k + 1][l + r] += num\)
因为根没有贡献,总路径条数就是两边加起来
-
\(2>\)第\(k + 1\)层的根贡献单点,则有
\(\large dp[k + 1][l + r + 1] += num\)和上边同理,但多了一个单点的贡献,所以我们加一,考虑这两个状态是相互独立的,我们只是在处理第\(k + 1\)层的所有情况,所以两个状态都是合法的
-
\(3>\)第\(k + 1\)层的根连接到左子树(或右子树)的某条路径上, 则有
\(\large dp[k + 1][l + r] += 2 * num * (l + r)\)
因为两个路径合成了一个大路径,所以\(l + r - 1\)少了一个,把括号拆开看\(2 * num * l + 2 * num * r\)就是把左右两边的贡献都加上,乘二是因为有方向,从\(1 -> 2\)和从\(2 -> 1\)不同,此时的边没有少,相当于减一又加一
-
\(4>\)第\(k + 1\)层的根连接左子树和右子树的各一条路径,则有
\(\large dp[k + 1][l + r - 1] += 2 * num * l * r\)
乘二还是因为有方向,这次将\(l * r\)是因为\(num\)是一个的方案数,但我有\(l + r\)个,所以应该累上,或者理解成一个\(l\)配\(r\)个\(r\),那\(l\)个\(l\)就是\(l * r\)
-
\(5>\)第\(k + 1\)层的根连接左子树(或右子树)的两条路径,则有
\(\large dp[k + 1][l + r - 1] += num * (l * (l - 1) + r * (r - 1))\)
此时一个子树里连了两个边,我们这时考虑的一定是经过根节点的,因为不经过的已经在上边被考虑过了,所以此时我们应该有\(C_{l}^{2}\)种方案(先考虑左子树),即是从一个左子树内的点到根再回到一个左子树内的点,又因为有方向,所以再乘以二,就成了\(l * (l - 1)\),右子树同理
-
here
#include <bits/stdc++.h>
#define LL long long
#define Re register int
#define LD long double
#define mes(x, y) memset(x, y, sizeof(x))
#define cpt(x, y) memcpy(x, y, sizeof(x))
#define fuc(x, y) inline x y
#define fr(x, y, z)for(Re x = y; x <= z; x ++)
#define fp(x, y, z)for(Re x = y; x >= z; x --)
#define frein(x) freopen(#x ".in", "r", stdin)
#define freout(x) freopen(#x ".out", "w", stdout)
#define ki putchar('\n')
#define fk putchar(' ')
#define WMX aiaiaiai~~
#define pr pair<long long, long long>
#define mk(x, y) make_posair(x, y)
using namespace std;
namespace kiritokazuto{
auto read = [](){
LL x = 0;
int f = 1;
char c;
while (!isdigit(c = getchar())){ if (c == '-')f = -1; }
do{ x = (x << 1) + (x << 3) + (c ^ 48); } while (isdigit(c = getchar()));
return x * f;
};
template <typename T> fuc(void, write)(T x){
if (x < 0)putchar('-'), x = -x;
if (x > 9)write(x / 10); putchar(x % 10 | '0');
}
}
using namespace kiritokazuto;
const int maxn = 410, Mod = 1e9 + 7;
const int Inf = 2147483647;
#define int long long
int n;
int dp[1010][1010];
LL p = 0;
signed main(){
n = read(), p = read();
dp[1][0] = dp[1][1] = 1;
fr(i, 1, n - 1){
fr(l, 0, n){
for (Re r = 0;l + r - 1 <= n; r++){
LL num = dp[i][l] * dp[i][r] % p;
dp[i + 1][l + r] = (dp[i + 1][l + r] + (2 * (l + r) % p + 1) % p * num) % p;
dp[i + 1][l + r + 1] = (dp[i + 1][l + r + 1] + num) % p;
if (l + r)dp[i + 1][l + r - 1] = (dp[i + 1][l + r - 1] + 2ll * num * l % p * r % p) % p, dp[i + 1][l + r - 1] = (dp[i + 1][l + r - 1] + num * (l * (l - 1) % p + r * (r - 1) % p) % p) % p;
}
}
}
write(dp[n][1] % p);
return 0;
}
求和
签到题,没啥好说的...话说我暴力跑的好快啊,注释掉的是暴力,其实就是预处理一下,然后差分就行
here
#include <bits/stdc++.h>
#define LL long long
#define Re register int
#define LD long double
#define mes(x, y) memset(x, y, sizeof(x))
#define cpt(x, y) memcpy(x, y, sizeof(x))
#define fuc(x, y) inline x y
#define fr(x, y, z)for(Re x = y; x <= z; x ++)
#define fp(x, y, z)for(Re x = y; x >= z; x --)
#define frein(x) freopen(#x ".in", "r", stdin)
#define freout(x) freopen(#x ".out", "w", stdout)
#define ki putchar('\n')
#define fk putchar(' ')
#define WMX aiaiaiai~~
#define pr pair<long long, long long>
#define mk(x, y) make_posair(x, y)
using namespace std;
namespace kiritokazuto{
auto read = [](){
LL x = 0;
int f = 1;
char c;
while (!isdigit(c = getchar())){ if (c == '-')f = -1; }
do{ x = (x << 1) + (x << 3) + (c ^ 48); } while (isdigit(c = getchar()));
return x * f;
};
template <typename T> fuc(void, write)(T x){
if (x < 0)putchar('-'), x = -x;
if (x > 9)write(x / 10); putchar(x % 10 | '0');
}
}
using namespace kiritokazuto;
const int maxn = 300100, Mod = 998244353;
const int Inf = 2147483647;
//虽然但是,D题看着确实好欺负
//先莽个暴力
//又额树剖干上了
struct Node{
int to, next;
}wmx[maxn << 1];
LL head[maxn], len = 0;
fuc(void, Qian)(int from, int to){
wmx[++len].to = to;
wmx[len].next = head[from];
head[from] = len;
}
int k, n, m;
LL ans;
LL top[maxn], sz[maxn], son[maxn], dep[maxn], fa[maxn];
LL Maxdep = -1;
fuc(void, dfs1) (int x, int pre){
sz[x] = 1;
if (x == 1)dep[x] = 0;
else dep[x] = dep[pre] + 1;
fa[x] = pre;
Maxdep = max(Maxdep, dep[x]);
for (Re i = head[x]; i; i = wmx[i].next){
int to = wmx[i].to;
if (to == pre)continue;
dfs1(to, x);
sz[x] += sz[to];
if (sz[son[x]] < sz[to])son[x] = to;
}
}
fuc(void, dfs2) (int x, int tp){
top[x] = tp;
if (!son[x])return;
dfs2(son[x], tp);
for (Re i = head[x]; i; i = wmx[i].next){
int to = wmx[i].to;
if (to != fa[x] && to != son[x])dfs2(to, to);
}
}
fuc(int, get_lca)(int x, int y){
if (top[x] == top[y]){
return (dep[x] < dep[y]) ? x : y;
}
while (top[x] != top[y]){
if (dep[top[x]] < dep[top[y]])swap(x, y);
x = fa[top[x]];
}
// printf("x == %d y == %d\n", x, y);
return (dep[x] < dep[y]) ? x : y;
}
LL Pow[maxn][51];
fuc(void, init)(LL x){
fr(i, 1, x)Pow[i][1] = i;//所有dep自己的
fr(i, 1, x){
fr(j, 2, 50){
Pow[i][j] = (Pow[i][j - 1] * i) % Mod;
//累乘
}
}
fr(j, 1, 50){
fr(i, 1, x){
Pow[i][j] = (Pow[i][j] + Pow[i - 1][j]) % Mod;
//链前缀和
}
}
}
// fuc(LL, qpow)(LL a, LL b){
// LL res = 1;
// while (b){
// if (b & 1) res = (res * a) % Mod;
// a = (a * a) % Mod;
// b >>= 1;
// }
// return res % Mod;
// }
//疏忽了,k <= 50打个表就行....qpow太慢了
//可以类比一下那个dis的操作
/*
这拍了一下,好像也没快多少....
1900 -> 1800
保佑能卡过去!
*/
signed main(){
// frein(data);
// freout(std);
n = read();
fr(i, 1, n - 1){
int x = read(), y = read();
Qian(x, y);
Qian(y, x);
}
dfs1(1, 0);
dfs2(1, 1);
//ri dfs2写成dfs1了,浪费半个小时
m = read();
// fr(i, 1, n){
// printf("dep[%d] = %d top[%d] = %d\n", i, dep[i], i, top[i]);
// }
init(Maxdep);
fr(i, 1, m){
ans = 0;
int x = read(), y = read(), k = read();
int lca = get_lca(x, y);
ans = Pow[dep[x]][k] + Pow[dep[y]][k] - Pow[dep[lca]][k];
if (dep[lca] > 1)ans -= Pow[dep[lca] - 1][k];
ans = (ans % Mod + Mod) % Mod;
// ans = (ans + qpow(dep[lca], k)) % Mod;
// int st = 0;
// st = (dep[x] < dep[y]) ? x : y;
// int ed = 0;
// ed = (st == x) ? y : x;
// // printf("lca = %d st = %d ed = %d ans = %lld dep[%d] = %d\n", lca, st, ed, ans, lca, dep[lca]);
// if (top[x] != top[y])fr(j, dep[lca] + 1, dep[st]) ans = (ans + 2 * qpow(j, k)) % Mod;
// else fr(j, dep[lca] + 1, dep[st]) ans = (ans + qpow(j, k)) % Mod;
// // printf("now ans = %lld \n", ans);
// fr(j, dep[st] + 1, dep[ed]) ans = (ans + qpow(j, k)) % Mod;
write(ans);
ki;
}
return 0;
}
/*
5
1 2
1 3
2 4
2 5
2
1 4 5
5 4 45
*/

![暑假集训五[星际旅行, 砍树, 超级树, 求和]](https://img2022.cnblogs.com/blog/2205491/202209/2205491-20220930065154345-1792396788.png) 暑假集训五
暑假集训五
