算法导论(第24章 单源最短路径)
第24章 单源最短路径
问题描述
给定一个带权重的有向图\(G = (V, E)\)和权重函数\(w: E → R\),该权重函数将每条边映射到实数值的权重上(当然可能存在负权)。
图中一条路径\(p = <v_0, …, v_k>\)的权重\(w(p)\)是构成该路径的所有边的权重之和:\(w(p) = \sum_{i = 1}^{k}w(v_{i - 1}, v_i)\)。
定义从结点\(u\)到结点\(v\)的最短路径权重\(\delta(u, v)\)如下:
\(\delta(u, v) = min\{w(p): u → v\}\)——如果存在一条从结点\(u\)到结点\(v\)的路径
\(\delta(u, v) = \infty\)——其他
从结点\(u\)到结点\(v\)的最短路径则定义为任何一条权重为\(w(p) = \delta(u, v)\)的从\(u\)到\(v\)的路径\(p\)。
22.2节讨论的广度优先搜索算法就是一个求取最短路径的算法,但该算法只能用于无权重的图。
最短路径的几个变体
- 单源最短路径问题
- 单目的地最短路径问题
- 单结点对最短路径问题
- 所有结点对最短路径问题
最短路径的最优子结构
最短路径算法通常依赖最短路径的一个重要性质:两个结点之间的一条最短路径包含着其他的最短路径。
而最优子结构是可以使用动态规划(第15章)和贪心算法(第16章)的一个重要指标。相应的,后面在24.3节讨论的\(Dijkstra\)算法就是一个贪心算法,在25.2节讨论的\(Floyd-Warshall\)算法则是一个动态规划算法。
- 引理24.1(最短路径的子路径也是最短路径)
负权重的边
环路
最短路径的表示
松弛操作
最短路径和松弛操作的性质
-
三角不等式性质
-
上界性质
-
非路径性质
-
收敛性质
-
路径松弛性质
-
前驱子图性质
本章概要
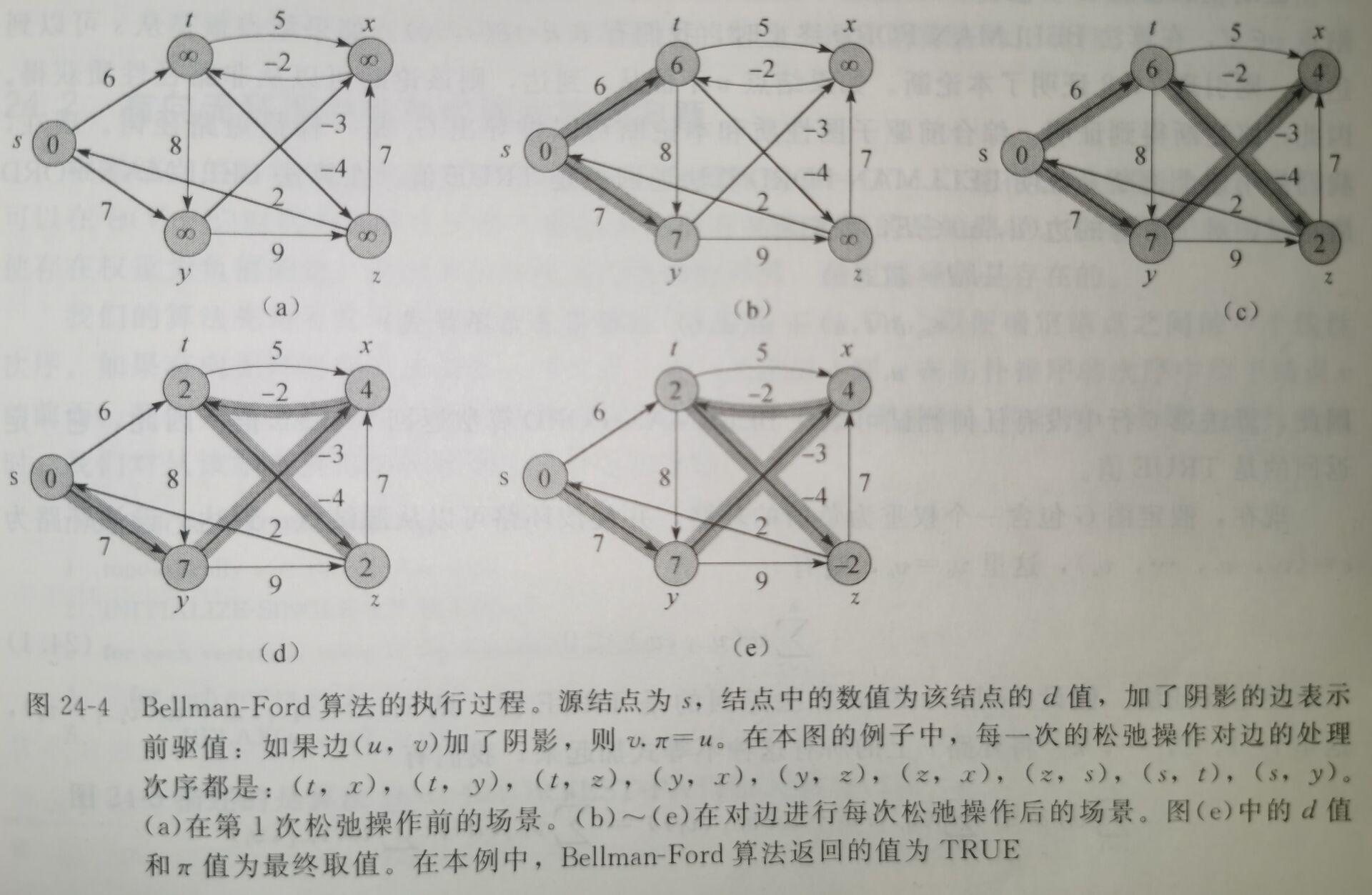
24.1节讨论\(Bellman-Ford\)算法,该算法解决的是一般情况下的单源最短路径问题(边的权重可以为负值)。\(Bellman-Ford\)算法还能够侦测是否存在从源结点可以到达的权重为负值的环路。
24.2节给出在有向无环图中计算单源最短路径的线性时间的算法。
24.3节讨论\(Dijkstra\)算法,该算法的时间复杂度低于\(Bellman-Ford\)算法,但要求边的权重为非负值。
24.4节描述如何使用\(Bellman-Ford\)算法来解决线性规划中的一种特殊情况。
24.5节给出最短路径和松弛操作的性质的证明。
本章所讨论的所有算法都假定有向图\(G\)以邻接链表的方式予以存放。此外,边的权重与边本身存放在一起,这样在遍历每条邻接链表时,我们可以在\(O(1)\)时间内获得边的权重。
24.1 \(Bellman-Ford\)算法
\(Bellman-Ford\)算法解决的是一般情况下的单源最短路径问题,在这里,边的权重可以为负值。
给定带权重的有向图\(G = (V, E)\)和权重函数\(w: E → R\),\(Bellman-Ford\)算法返回一个布尔值,以表明是否存在一个从源结点可以到达的权重为负值的环路。如果存在这样一个环路,算法将告诉我们不存在解决方案。如果没有这种环路存在,算法将给出最短路径和它们的权重。
\(Bellman-Ford\)算法通过对边进行松弛操作来渐近地降低从源结点\(s\)到每个结点\(v\)的最短路径的估计值\(v.d\),直到该估计值与实际的最短路径权重\(\delta(u, v)\)相同为止。
BELLMAN-FORD(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 for i = 1 to |G.V| - 1
3 for each edge(u, v) ∈ G.E
4 RELAX(u, v, w)
5 for each edge(u, v) ∈ G.E
6 if v.d > u.d + w(u, v)
7 return FALSE
8 return TRUE
- 算法第1行对所有结点的\(d\)值和\(\pi\)值进行初始化。
- 算法第2~4行对每条边进行\(|V| - 1\)次松弛操作。
- 算法第5~8行检查图中是否存在权重为负值的环路并返回与之相应的布尔值。
\(Bellman-Ford\)算法的复杂度为\(O(VE)\)。
24.2 有向无环图中的单源最短路径问题
24.3 \(Dijkstra\)算法
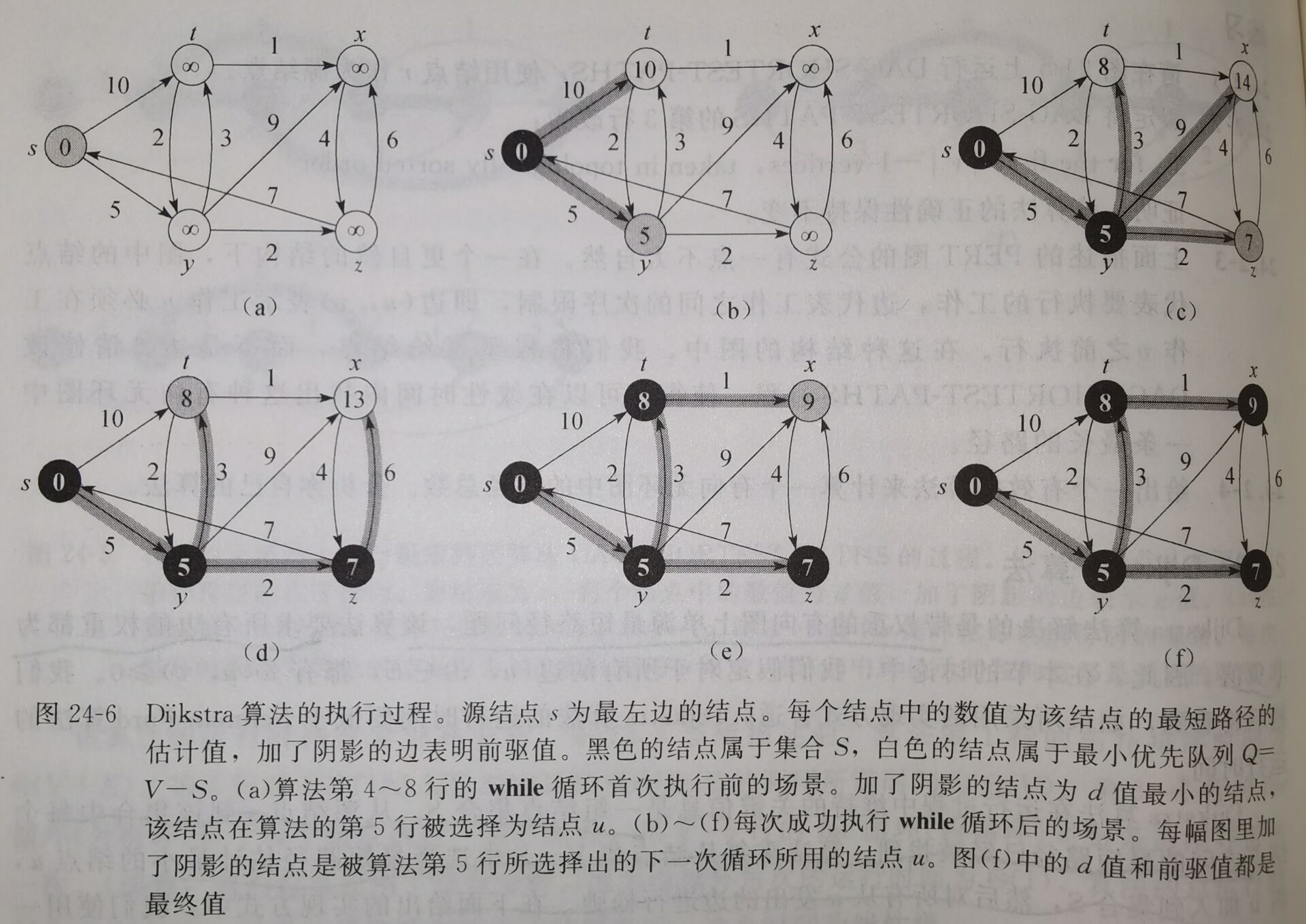
\(Dijkstra\)算法解决的是带权重的有向图上单源最短路径问题,该算法要求所有边的权重都为非负值。
\(Dijkstra\)算法在运行过程中维持的关键信息是一组结点集合\(S\)。从源结点\(s\)到该集合中每个结点之间的最短路径已经被找到。算法重复从结点集\(V - S\)中选择最短路径估计最小的结点\(u\),将\(u\)加入到集合\(S\),然后对所有从\(u\)发出的边进行松弛(这里使用一个最小优先队列\(Q\)来保存结点集合,每个结点的关键值为其\(d\)值)。
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 S = Ø
3 Q = G.V
4 while Q ≠ Ø
5 u = EXTRACT-MIN(Q)
6 S = S ∪ {u}
7 for each vertex v ∈ G.Adj[u]
8 RELAX(u, v, w)
- 算法第1行执行的同样是\(d\)值和\(\pi\)值进行初始化。
- 算法第2行将集合\(S\)初始化为一个空集。
- 算法第3行对最小优先队列\(Q\)进行初始化。(算法所维持的不变式为\(Q = V - S\))
- 算法第4~8行从\(Q\)中抽取结点\(u\)并加入到\(S\)中,对所有从结点\(u\)发出的边\((u, v)\)进行松弛操作。
\(Dijkstra\)算法的复杂度依赖于最小优先队列的实现。
- 如果采用数组,则复杂度为\(O(V^2)\)
- 如果采用二叉堆,则复杂度为\(O((V + E)\lg{V})\)(若所有结点都可以从源结点到达,则该时间为\(O(E\lg{V})\))
- 如果采用斐波那契堆,则可改善为\(O(Vlog{V} + E)\)
24.4 差分约束和最短路径
24.5 最短路径性质的证明
-
引理24.11(上界性质) 设\(G = (V, E)\)为一个带权重的有向图,权重函数为\(w: E → R\),源结点为\(s\),该图由算法\(INITIALIZE-SINGLE-SOURCE(G, s)\)执行初始化。那么对于所有的结点\(v \in V\),\(v.d \geqslant \delta(s, v)\),并且该不等式在对图\(G\)的边进行任何次序的松弛过程中保持成立。而且一旦\(v.d\)取得其下界\(\delta(s, v)\)后,将不再发生变化。
-
引理24.13(收敛性质) 设\(G = (V, E)\)为一个带权重的有向图,权重函数为\(w: E → R\)。设\(s \in V\)为某个源结点,\(s → u → v\)为图\(G\)中的一条最短路径,这里\(u, v \in V\)。假定图\(G\)由\(INITIALIZE-SINGLE-SOURCE(G, s)\)算法进行初始化,并在这之后进行了一系列边的松弛操作,其中包括对边\((u, v)\)的松弛操作\(RELAX(u, v, w)\)。如果在对边\((u, v)\)进行松弛操作之前的任意时刻有\(u.d = \delta(s, u)\),则在该松弛操作之后的所有时刻有\(v.d = \delta(s, v)\)。
证明:根据上界性质——如果在对边\((u, v)\)进行松弛前的某个时刻有\(u.d = \delta(s, u)\),则该等式在松弛操作后仍然成立。所以松弛操作之后,仍然有\(u.d = \delta(s, u)\)。
根据最优子结构的性质,在对边\((u, v)\)进行松弛后,有\(v.d \leqslant u.d + w(u, v) = \delta(s, u) + w(u, v) = \delta(s, v)\)
又根据上界性质,我们有\(v.d \geqslant \delta(s, v)\)。
由夹逼定理:\(v.d = \delta(s, v)\),并且该等式在此之后一直保持成立。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号