算法导论(第23章 最小生成树)
第23章 最小生成树
问题描述
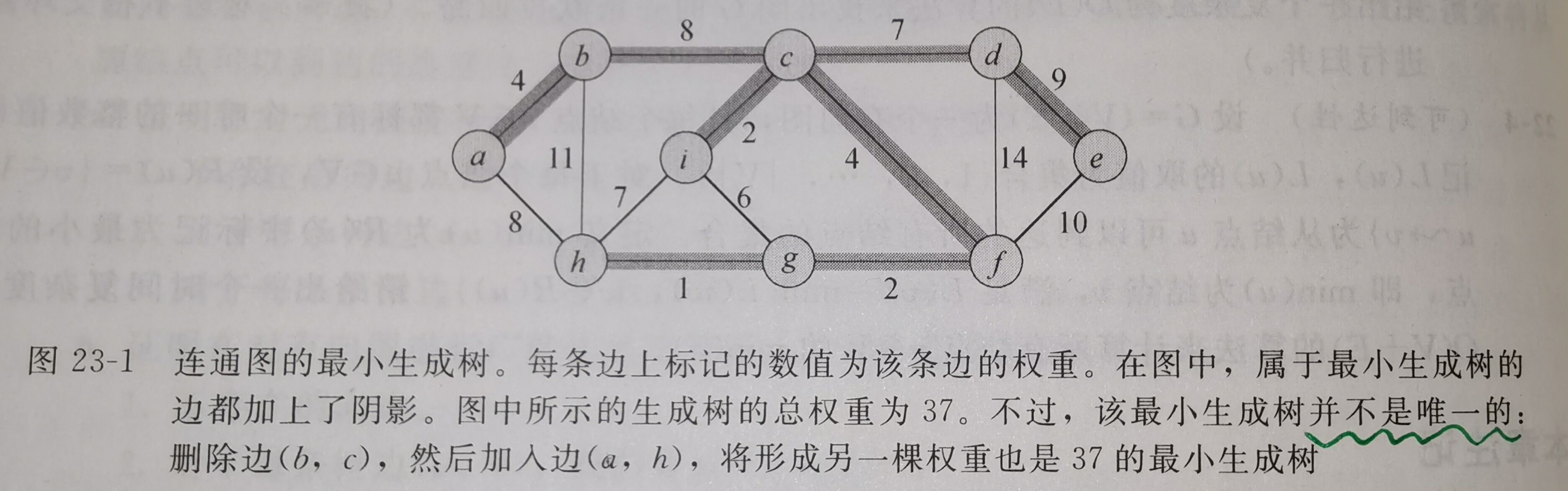
对于一个连通无向图\(G = (V, E)\),为其每条边\((u, v) \in E\),赋予权重\(w(u, v)\)。我们希望找到一个无环子集\(T \subset E\),既能够将所有结点连接起来,又具有最小权重,即\(w(T) = \sum_{(u, v) \in T}w(u, v)\)的值最小。
由于\(T\)是无环的,并且连通所有的结点,因此,\(T\)必然是一棵树。我们称这样的树为(图\(G\)的)生成树,因为它是由图\(G\)所生成的。我们称求取该生成树的问题为最小生成树问题。
对于求解最小生成树问题的两种算法:\(Kruskal\)算法和\(Prim\)算法。如果使用普通的二叉堆,那么可以容易地将这两个算法的时间复杂度限制在\(O(E\lg{V})\)的数量级内。但如果使用斐波那契堆,\(Prim\)算法的运行时间将改善为\(O(E + V\lg{V})\)。此运行时间在\(|V|\)远远小于\(|E|\)的情况下较二叉堆有很大改进。
上述两种最小生成树算法都是贪心算法。
23.1 最小生成树的形成
两种算法使用的贪心策略可以通用地表述为:在每个时刻生长最小生成树的一条边,并在整个策略的实施过程中,管理一个遵循下述循环不变式的边集合\(A\)——在每遍循环之前,\(A\)是某棵最小生成树的一个子集。
在每一步,我们要做的事情是:选择一条边\((u, v)\),将其加入到集合\(A\)中,使得\(A\)不违反循环不变式(即\(A∪{(u, v)}\)也是某棵最小生成树的子集)。由于我们可以安全地将这种边加入到集合\(A\)而不会破坏\(A\)的循环不变式,因此这样的边为集合\(A\)的安全边。
GENERIC-MST(G, w)
1 A = Ø // init
2 while A does not form a spanning tree // hold
3 find an edge(u, v) that is safe for A
4 A = A ∪ {(u, v)}
5 return A // end
下面将介绍辨认安全边的规则(定理 23.1)。
首先给出一些定义:
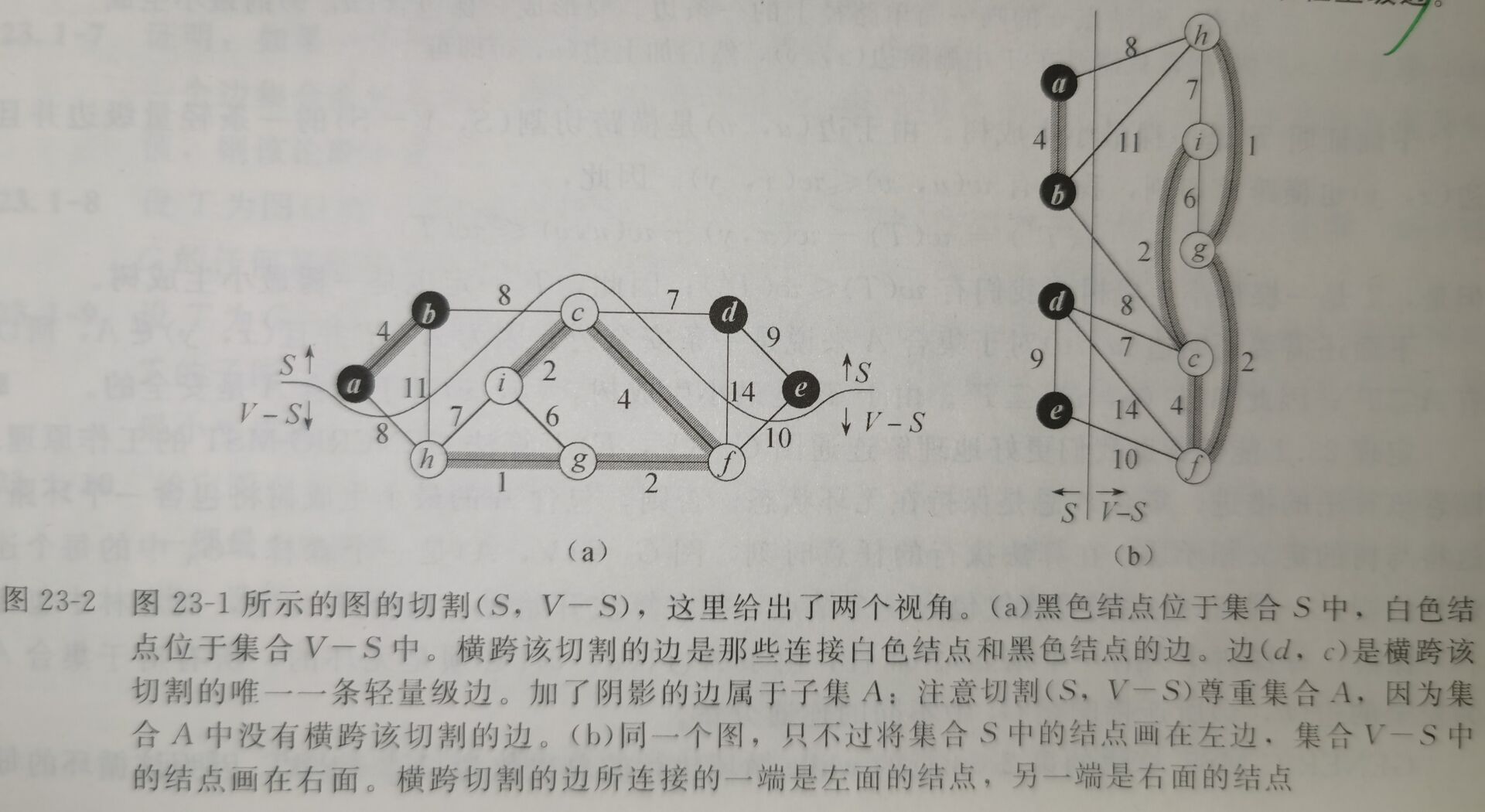
- 无向图\(G = (V, E)\)的一个切割\((S, V - S)\)是集合\(V\)的一个划分。
- 如果一条边\((u, v) \in E\)的一个端点位于集合\(S\),另一个端点位于集合\(V - S\),则称该条边横跨切割\((S, V - S)\)。
- 如果集合\(A\)中不存在横跨该切割的边,则称该切割尊重集合\(A\)。
- 在横跨一个切割的所有边中,权重最小的边称为轻量级边(不一定唯一)。
- *如果一条边是满足某个性质的所有边中权重最小的,则称该条边是满足给定性质的一条轻量级边。
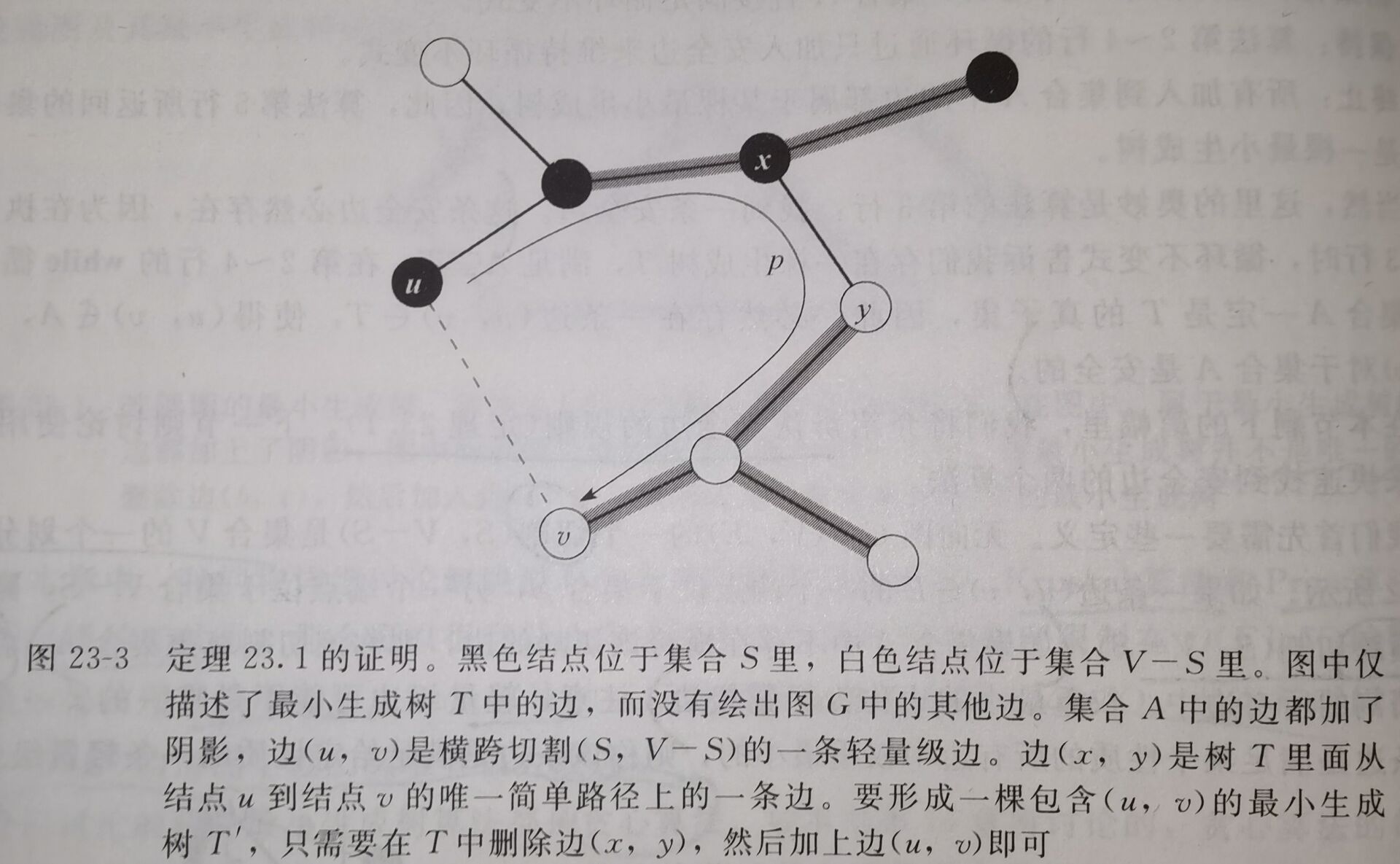
- 定理 23.1 设\(G = (V, E)\)是一个在边\(E\)上定义了实数值权重函数\(w\)的连通无向图。设集合\(A\)为\(E\)的一个子集,且\(A\)包括在图\(G\)的某棵最小生成树中,设\((S, V - S)\)是图\(G\)中尊重集合\(A\)的任意一个切割,又设\((u, v)\)是横跨切割\((S, V - S)\)的一条轻量级边。那么边\((u, v)\)对于集合\(A\)是安全的。
23.2节中的两个算法将使用定理 23.1的下列推论:
- 推论 23.2 设\(G = (V, E)\)是一个在边\(E\)上定义了实数值权重函数\(w\)的连通无向图。设集合\(A\)为\(E\)的一个子集,且\(A\)包括在图\(G\)的某棵最小生成树中,并设\(C = (V_C, E_C)\)为森林\(G_A = (G, A)\)中的一个连通分量(树)。如果边\((u, v)\)是连接\(C\)和\(G_A\)中某个其他连通分量的一条轻量级边。那么边\((u, v)\)对于集合\(A\)是安全的。
证明:切割\((V_C, V - V_C)\)尊重集合\(A\),边\((u, v)\)是横跨该切割的一条轻量级边,因此边\((u, v)\)对于集合\(A\)是安全的。
23.2 \(Kruskal\)算法和\(Prim\)算法
两种算法都使用一条具体的规则来确定GENERIC-MST算法第3行所描述的安全边。
- 在\(Kruskal\)算法中,集合\(A\)是一个森林,其结点就是给定图的结点。每次加入到集合\(A\)中的安全边永远是权重最小的连接两个不同分量的边。
- 在\(Prim\)算法中,集合\(A\)则是一棵树。每次加入到\(A\)中的安全边永远是连接\(A\)和\(A\)之外某个结点的边中权重最小的边。
\(Kruskal\)算法
在所有连接森林中两棵不同树的边里面,找到权重最小的边\((u, v)\)。
设\(C_1\)和\(C_2\)为边\((u, v)\)所连接的两棵树。由于边\((u, v)\)一定是连接\(C_1\)和其他某棵树的一条轻量级边,由推论23.2可知边\((u, v)\)是\(C_1\)的一条安全边。很显然\(Kruskal\)算法属于贪心算法。
MST-KRUSKAL(G, w)
1 A = Ø
2 for each vertex v ∈ G.V
3 MAKE-SET(v)
4 sort the edges of G.E into nondecreasing order by weight w
5 for each edge (u, v) ∈G.E, taken in nondecreasing order by weight
6 if FIND-SET(u) ≠ FIND-SET(v)
7 A = A ∪ {(u, v)}
8 UNION(u, v)
9 return A
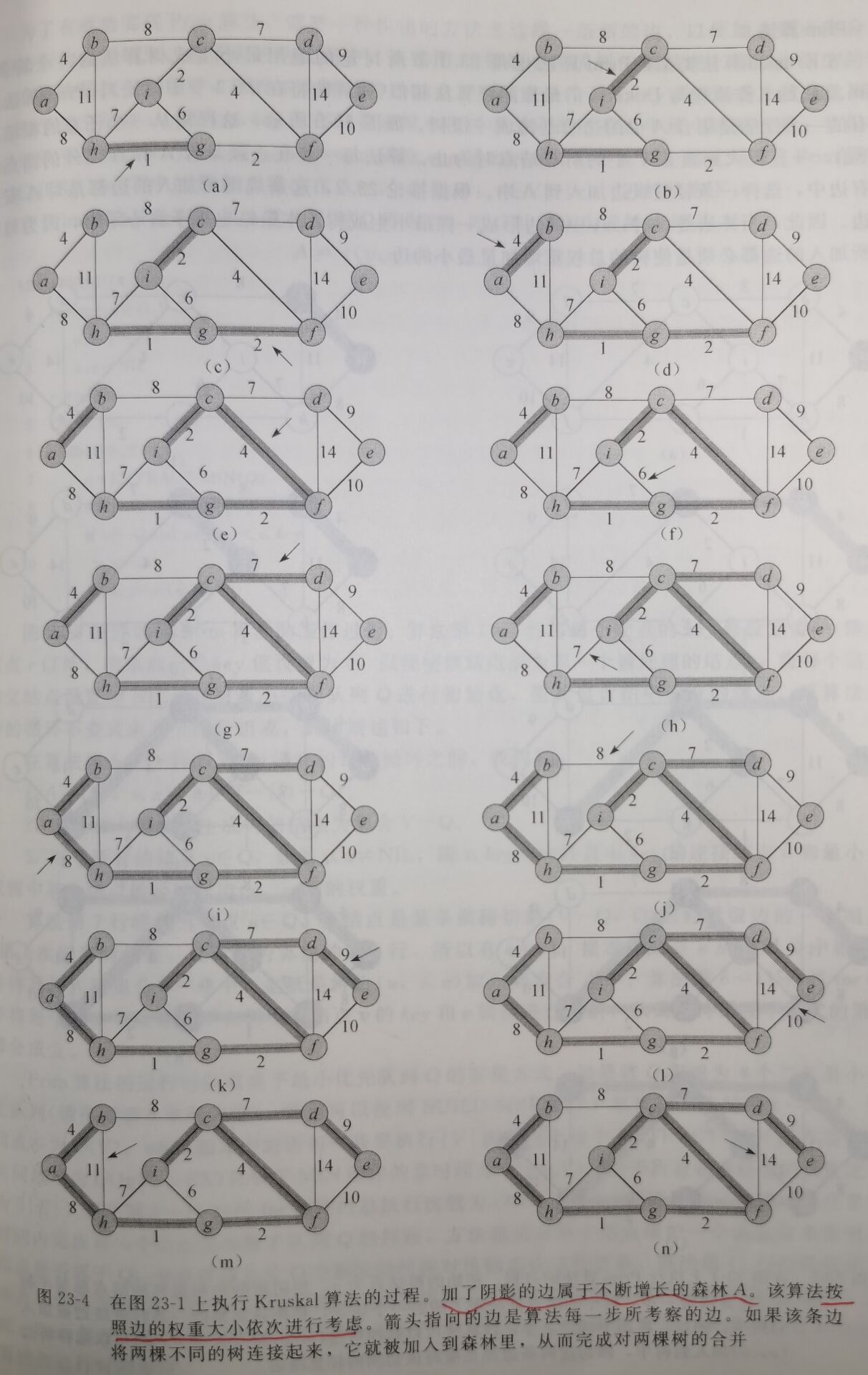
该算法的实现与21.1节所讨论的计算连通分量的算法类似。使用一个不相交集合数据结构来维护几个互不相交的元素集合。每个集合代表当前森林中的一棵树。
- 算法的1~3行将集合\(A\)初始化为空集,并创建\(|V|\)棵树,每棵树仅包含一个结点。
- 算法的5~8行的for循环安装权重从低到高的次序遍历边。对于每条边\((u, v)\)来说,检查端点\(u\)和端点\(v\)是否属于同一棵树。如果是,该条边不能加入到森林里;如果不是,则两个端点分别术语不同的树,算法第7行将把这条边加入到集合\(A\)中,第8行则将两棵树中的结点进行合并。
\(Kruskal\)算法的复杂度为\(O(E\lg{V})\)
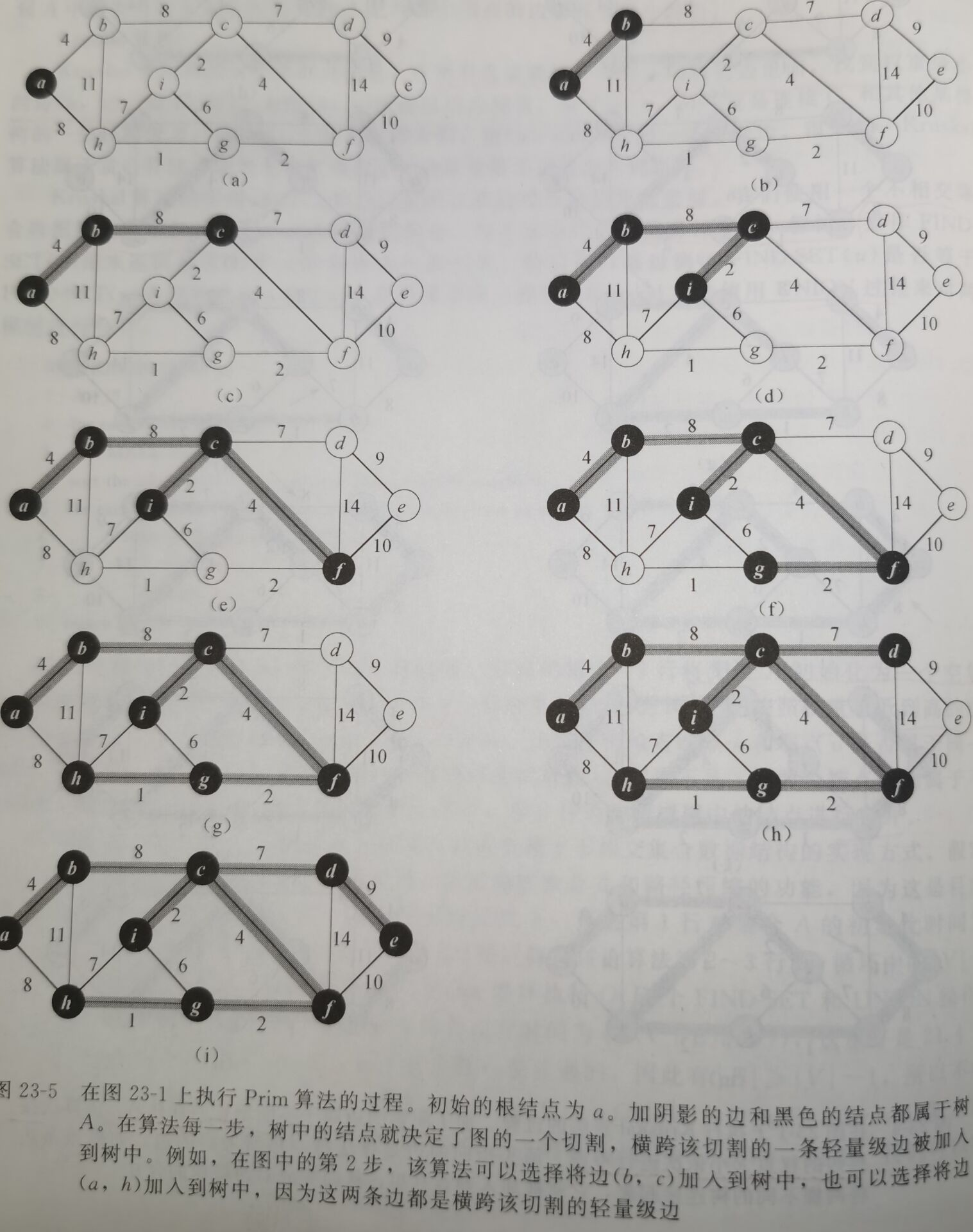
\(Prim\)算法
在所有连接集合\(A\)和\(A\)之外的结点的所有边中,选择一条轻量级边加入到\(A\)中。
同样的,根据推论23.2,上述算法规则所加入的边都是对\(A\)安全的边,因此,当算法终止时,\(A\)中的边形成一棵最小生成树。很显然\(Prim\)算法也属于贪心算法。
MST-PRIM(G, w, r)
1 for each u ∈ G.V
2 u.key = ∞
3 u.π = NIL
4 r.key = 0
5 Q = G.V
6 while Q ≠ Ø
7 u = EXTRACT-MIN(Q)
8 for each v ∈ G.Adj[u]
9 if v ∈ Q and w(u, v) < v.key
10 v.π = u
11 v.key = w(u, v)
连通图\(G\)和最小生成树的根结点\(r\)将作为算法的输入。在算法的执行过程中,所有不在树\(A\)中的结点都存放在一个基于\(key\)属性的最小优先队列\(Q\)中。对于每个结点\(v\),属性\(v.key\)保存的是连接\(v\)和树中结点的所有边中最小边的权重。属性\(v.π\)给出的是结点\(v\)在树中的父结点。
\(Prim\)算法将GENERIC-MST中的集合\(A\)维持在\(A = \{(v, v.π): v ∈ V - \{ r \} - Q\}\)的状态下。
当\(Prim\)算法终止时,最小优先队列\(Q\)将为空,而\(G\)的最小生成树\(A = \{(v, v.π): v ∈ V - \{ r \}\}\)。
- 算法的1~5行将除根结点之外的每个结点的\(key\)值设置为∞,将每个结点的父结点设置为\(NIL\),并对最小优先队列\(Q\)进行初始化,使其包含图中所有的结点。
- 算法的7行将找出结点\(u \in Q\),该结点是某条横跨切割\((V - Q, Q)\)的轻量级边的一个端点。接着将结点\(u\)从队列\(Q\)中删除,并将其加入到集合\(V - Q\)中,也就是将边\((u, u.π)\)加入到集合\(A\)中。
- 算法的8~11行的for循环将每个与\(u\)邻接但却不在树中的结点\(v\)的\(key\)和\(\pi\)属性进行更新。
\(Prim\)算法的运行时间取决于最小优先队列\(Q\)的实现方式:如果将\(Q\)实现为一个二叉最小优先队列,则复杂度为\(O(E\lg{V})\);如果使用斐波那契堆来实现最小优先队列\(Q\),则其复杂度将改进到\(O(E + V\lg{V})\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号