算法导论(第22章 基本的图算法)
第22章 基本的图算法
本章将介绍图的表示和图的搜索。
- 图的搜索指的是系统化地跟随图中的边来访问图中的每个结点。(可以用来发现图的结构)
可以结合数据结构与算法分析——C语言描述(第9章 图论算法)https://www.cnblogs.com/kirin-dev/p/Data-Structures_Chapter-9.html 食用。
22.1 图的表示
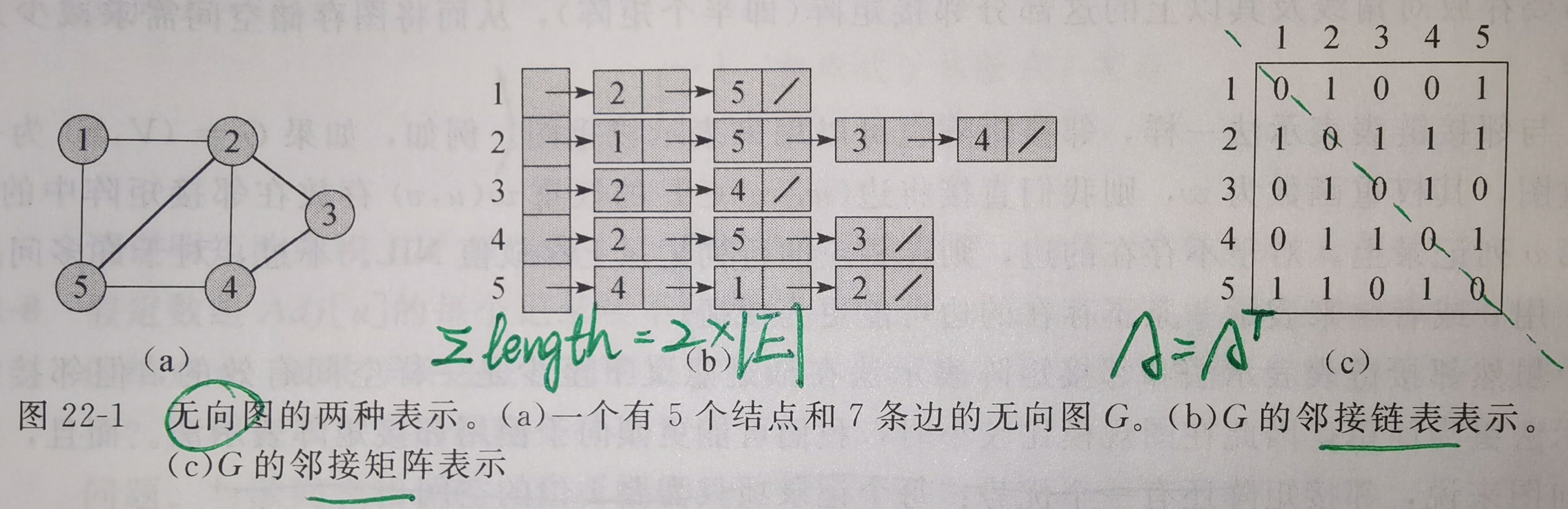
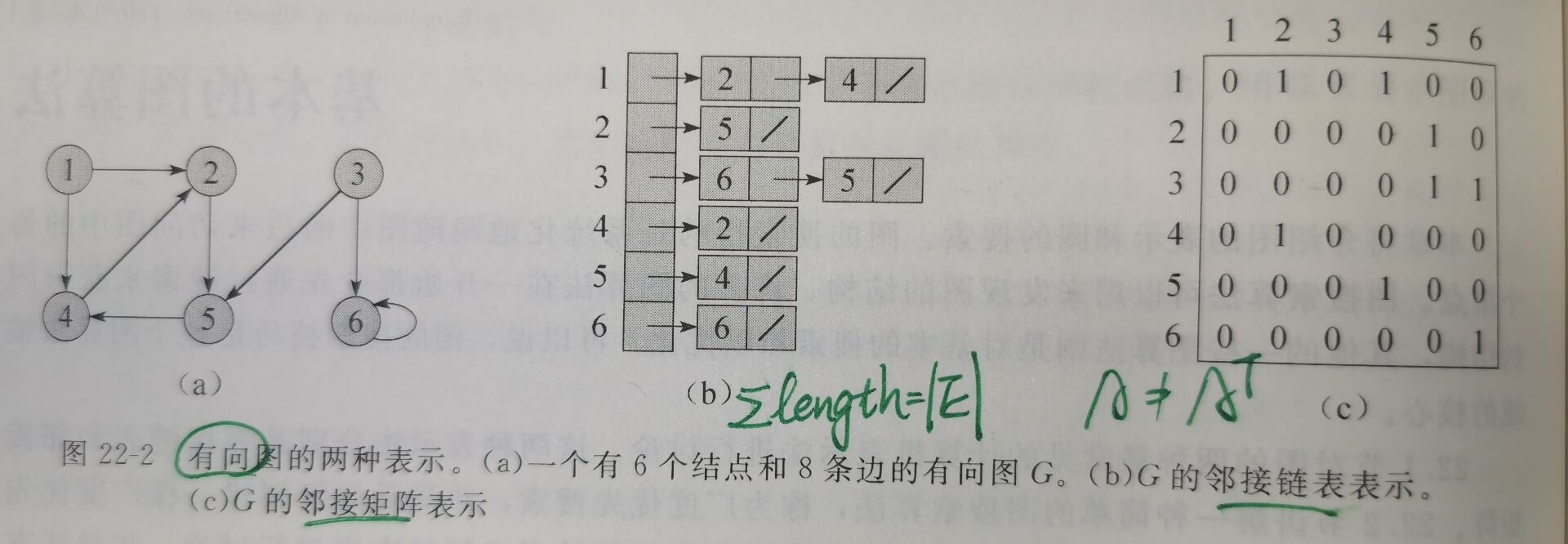
对于图\(G = (V, E)\),可以用两种标准表示方法表示。(既可以表示无向图,也可以表示有向图)
- 邻接链表的组合
- 邻接矩阵
稀疏图(边的条数\(|E|\)远远小于\(|V|^2\)的图)——邻接链表更紧凑。
稠密图(边的条数\(|E|\)接近\(|V|^2\)的图)/图规模较小/需要快速判断任意两个结点之间是否有边相连(第25章最短路径算法)——邻接矩阵。
邻接链表表示
对于图\(G = (V, E)\)来说,其邻接链表表示由一个包含\(|V|\)条链表的数组\(Adj\)所构成,每个结点有一条链表。
对于每个结点\(u \in V\),邻接链表\(Adj[u]\)包含所有与结点\(u\)之间有边相连的结点\(v\)——即\(Adj[u]\)包含图\(G\)中所有与\(u\)邻接的点。(伪代码中,将数组\(Adj\)看做是图的一个属性——\(G.Adj[u]\))
不管是有向图还是无向图,邻接链表表示法的存储空间需求均为\(\Theta(V + E)\)。
- 优势:鲁棒性很高,可以对其进行简单修改来支持许多其他的图变种(权重图)。
- 缺陷:无法快速判断\((u, v)\)是否是图中的一条边——需要进行一次搜索。
邻接矩阵表示
图\(G\)的邻接矩阵由一个\(|V| × |V|\)的矩阵\(A = (a_{ij})\)予以表示:
\(a_{ij} = 1——(i, j) \in E\)
\(a_{ij} = 0——(i, j) \notin E\)
邻接矩阵表示法的存储空间需求为\(\Theta(V^2)\)。而对于无向图,该需求可减少到原来的一般\(\Theta(V^2/2)\)——对称性。
-
优势:同样可以表示权重图;可以快速判断\((u, v)\)是否是图中的一条边;对于无向图而言,避免了数据冗余。
-
劣势:消耗更大的存储空间。
表示图的属性
对图进行操作的多数算法需要维持图中结点或边的某些属性。
在伪代码中,这些属性可以简单地通过在主体后加'.'并跟上属性名来表示。
在算法的实际程序中,则总需要额外分配空间来存放属性,或者通过面向对象的程序设计方式来实现(eg:结构体)。
22.2 广度优先搜索(BFS)
广度优先搜索是最简单的图搜索算法之一,也是许多重要的图算法的原型——Prim的最小生成树(23.2)和Dijkstra的单源最短路径算法(24.3)。
给定图\(G = (V, E)\)和一个可以识别的源结点\(s\),广度优先搜索对图\(G\)中的边进行系统性的探索来发现可以从源结点\(s\)到达的所有结点。
该算法能够计算从源结点\(s\)到每个可到达的结点的距离(最少的边数),同时生成一棵“广度优先搜索树”——该树以源结点\(s\)为根结点,包含所有可以从\(s\)到达的结点。
广度优先搜索之所以如此得名是因为该算法始终是将已发现结点和未发现结点之间的边界,沿其广度方向向外扩展。也就是说,算法需要在发现所距离源结点\(s\)为\(k\)的所有结点之后,才会发现距离源结点\(s\)为\(k + 1\)的其他结点。
为了跟踪算法的进展,广度优先搜索在概念上将每个结点涂上白色、灰色或黑色。所有结点在一开始的时候均涂上白色。第一次遇到一个结点就称该结点被发现。如果边\((u, v) \in E\)且结点\(u\)是黑色,则结点\(v\)既可能是灰色也可能是黑色——所有与黑色结点邻接的结点都已被发现,灰色结点邻接的结点中可能存在未被发现的白色结点(已知和未知的边界)。
广度优先搜索树:
- 根节点为源结点\(s\)。
- 在扫描已发现结点\(u\)的邻接链表时,每当发现一个白色结点\(v\),就将结点\(v\)和边\((u, v)\)同时加入该棵树中,称结点\(u\)是结点\(v\)的前驱或者父节点(每个结点最多只有一个父节点)。
- 如果结点\(u\)是从根结点\(s\)到结点\(v\)的简单路径上的一个结点,则结点\(u\)是结点\(v\)的祖先,结点\(v\)是结点\(u\)的后代。
该算法使用一个先进先出的队列\(Q\)来管理灰色结点集。
BFS(G, s)
1 for each vertex u ∈ G.V - {s}
2 u.color = WHITE // color
3 u.d = ∞ // distance
4 u.π = NIL // predecessor
5 s.color = GRAY
6 s.d = 0
7 s.π = NIL
8 Q = Ø
9 ENQUEUE(Q, s)
10 while Q ≠ Ø
11 u = DEQUEUE(Q)
12 for each v ∈ G.Adj[u]
13 if v.color == WHITE
14 v.color = GRAY
15 v.d = u.d + 1
16 v.π = u
17 ENQUEUE(Q, v)
18 u.color = BLACK
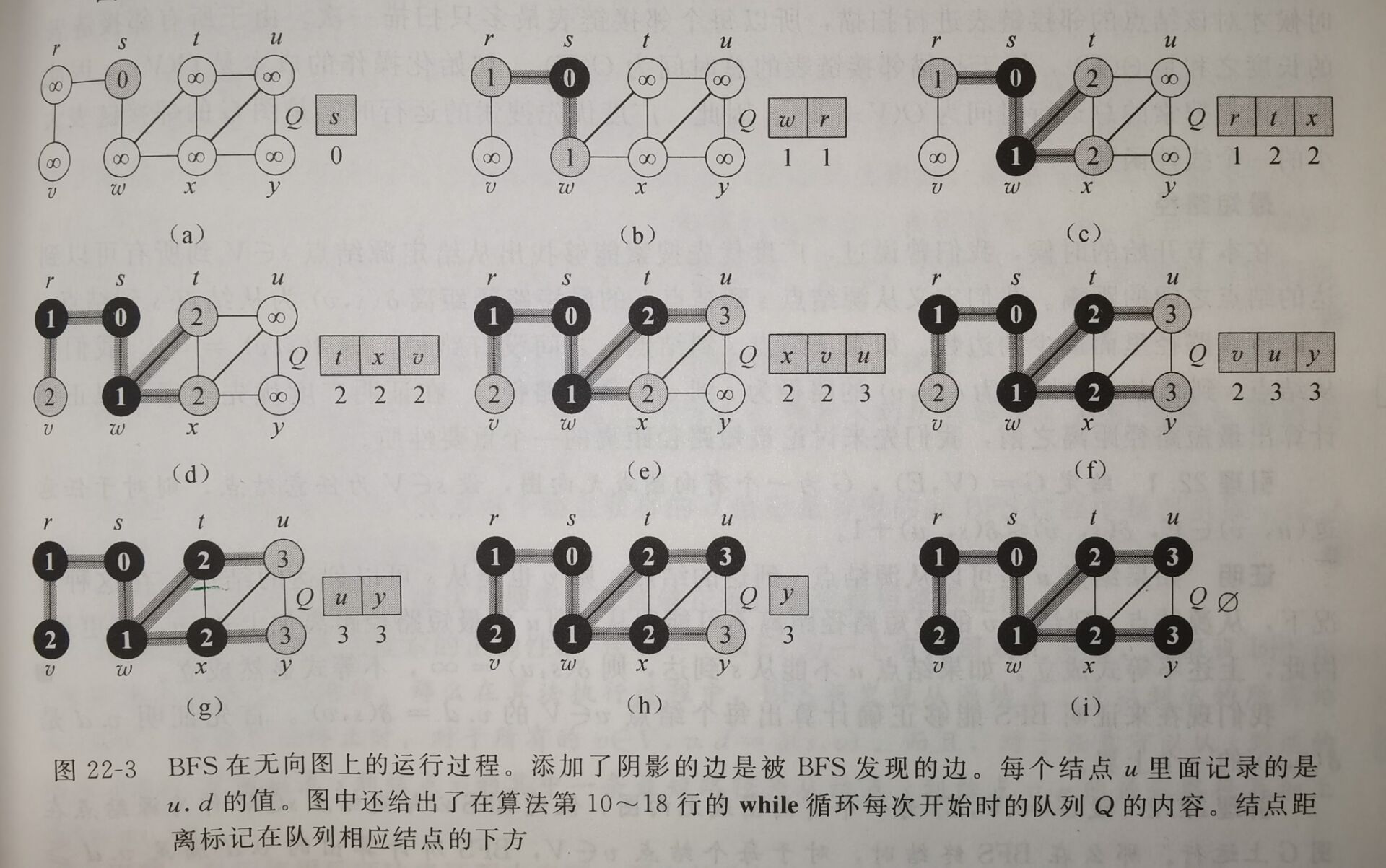
广度优先搜索的结果可能依赖于对每个结点的邻接结点的访问顺序:广度优先搜索树可能会不一样,但本算法所计算出来的距离\(d\)都是一样的。
广度优先搜索分析
- 入队出队:\(O(1) * V = O(V)\)
- 扫描邻接链表:\(O(E)\)
- 初始化:\(O(V)\)
广度优先搜索的运行时间:\(O(V + E)\)
最短路径
广度优先搜索树
22.3 深度优先搜索(DFS)
深度优先搜索之所以如此得名是因为它总是对最近才发现的结点\(v\)的出发边进行探索,直到该结点的所有出发边都被发现为止。(只要可能,就在图中尽量“深入”)一旦结点\(v\)的所有出发边都被发现,搜索则“回溯”到\(v\)的前驱结点,来搜索该前驱结点的出发边。该过程一直持续到从源结点可以达到的所有结点都被发现为止。如果还存在尚未发现的结点,则深度优先搜索将从这些未被发现的结点中任选一个作为新的源结点,并重复同样的搜索过程,直到图中所有结点都被发现为止。
与广度优先搜索不同的是,广度优先搜索的前驱子图形成一棵广度优先搜索树,深度优先搜索的前驱子图形成一个由多棵深度优先搜索树构成的深度优先搜索森林——搜索可能从多个源结点重复进行。
为了跟踪算法的进展,同样的,深度优先搜索在概念上将每个结点涂上白色、灰色或黑色。每个结点的初始颜色都是白色,在结点被发现后变为灰色,在其邻接链表被扫描完成后变为黑色。该方法可以保证每个结点仅在一棵深度优先搜索树中出现,因此,所有的深度优先搜索树是不相交的(disjoint)。
除了创建一个深度优先搜索森林外,深度优先搜索算法还在每个结点盖上一个时间戳。每个结点\(v\)由两个时间戳:第一个时间戳\(v.d\)记录结点\(v\)第一次被1发现的时间(涂上灰色的时间),第二个时间戳\(v.f\)记录搜索完成对\(v\)的邻接链表扫描的时间(涂上黑色的时间)——这能够帮助推断深度优先搜索算法的行为。
显然有\(v.d < v.f\),且都是处于\(1\)和\(2|V|\)之间的整数。
结点\(v\)在时刻\(v.d\)之前为白色,在时刻\(v.d\)和\(v.f\)之间为灰色,在时刻\(v.f\)之后为黑色。
在以下算法中,变量\(time\)是一个全局变量,用来计算时间戳。
DFS(G)
1 for each vertex u ∈ G.V
2 u.color = WHITE // color
3 u.π = NIL // predecessor
4 time = 0
5 for each vertex u ∈ G.V
6 if u.color == WHITE
7 DFS-VISIT(G, u)
DFS-VISIT(G, u)
1 time = time + 1 // white vertex u has just been discovered
2 u.d = time
3 u.color = GRAY
4 for each v ∈ G.Adj[u] // explore edge(u, v)
5 if v.color == WHITE
6 v.π = u
7 DFS-VISIT(G, v)
8 u.color = BLACK // blacken u; it is finished
9 time = time + 1
10 u.f = time
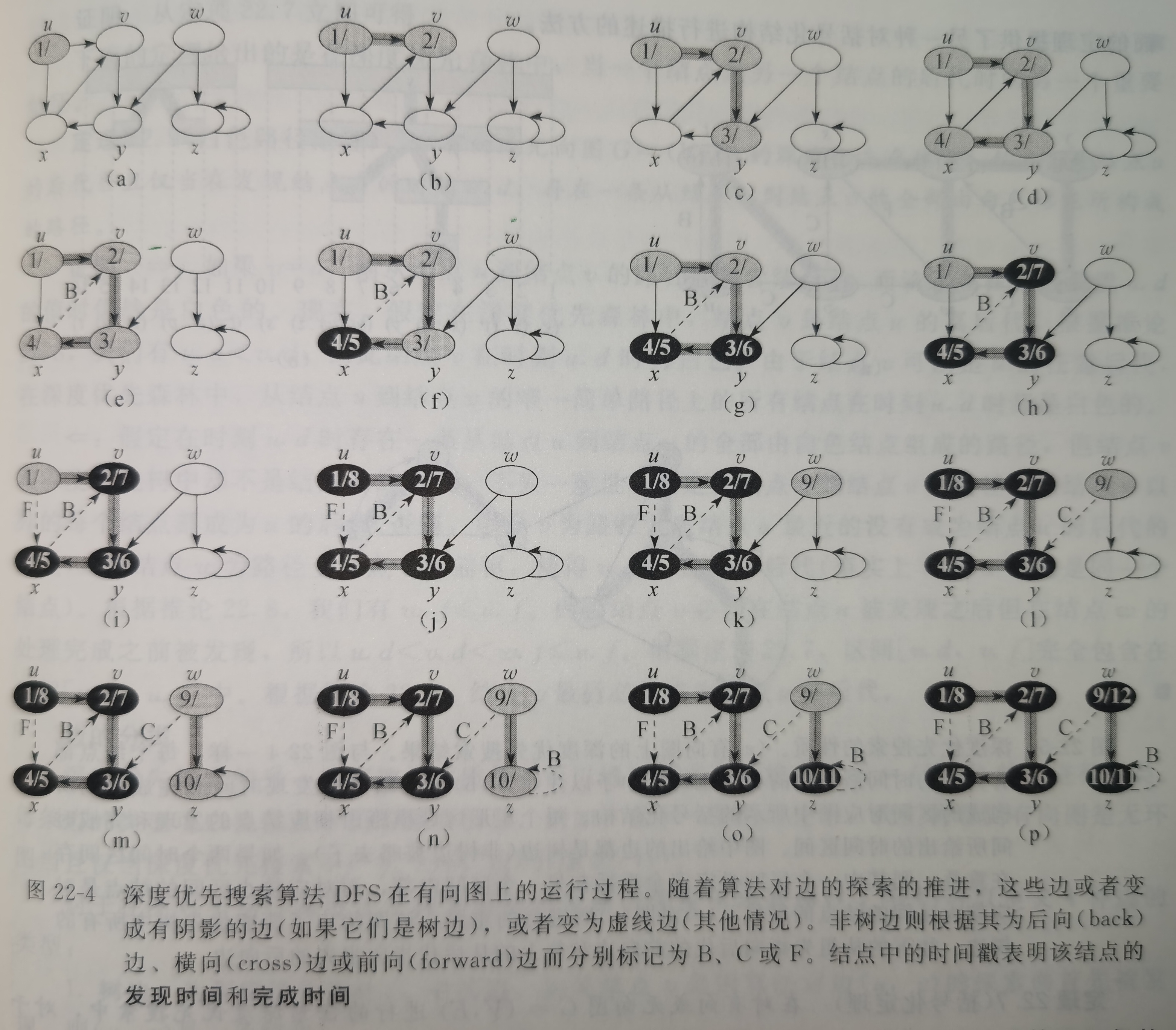
深度优先搜索分析
- 扫描图所用循环:\(\Theta(V)\)
- DFS-VISIT:\(\Theta(E)\)
深度优先搜索的运行时间:\(\Theta(V + E)\)
深度优先搜索的性质
深度优先搜索提供的是关于图结构的价值很高的信息。
-
深度优先搜索最基本的性质是:其生成的前驱子图\(G_π\)形成一个由多棵树所构成的森林,这是因为深度优先搜索树的结构与DFS-VISIT的递归调用结构完全对应(\(u = v.\pi\)当且仅当DFS-VISIT(G, v)在算法对结点\(u\)的邻接链表进行搜索时被调用)。
-
深度优先搜索的另一个重要性质是:结点的发现时间和完成时间具有所谓的括号化结构(parenthesis structure)。
边的分类
- 树边
- 后向边
- 前向边
- 横向边
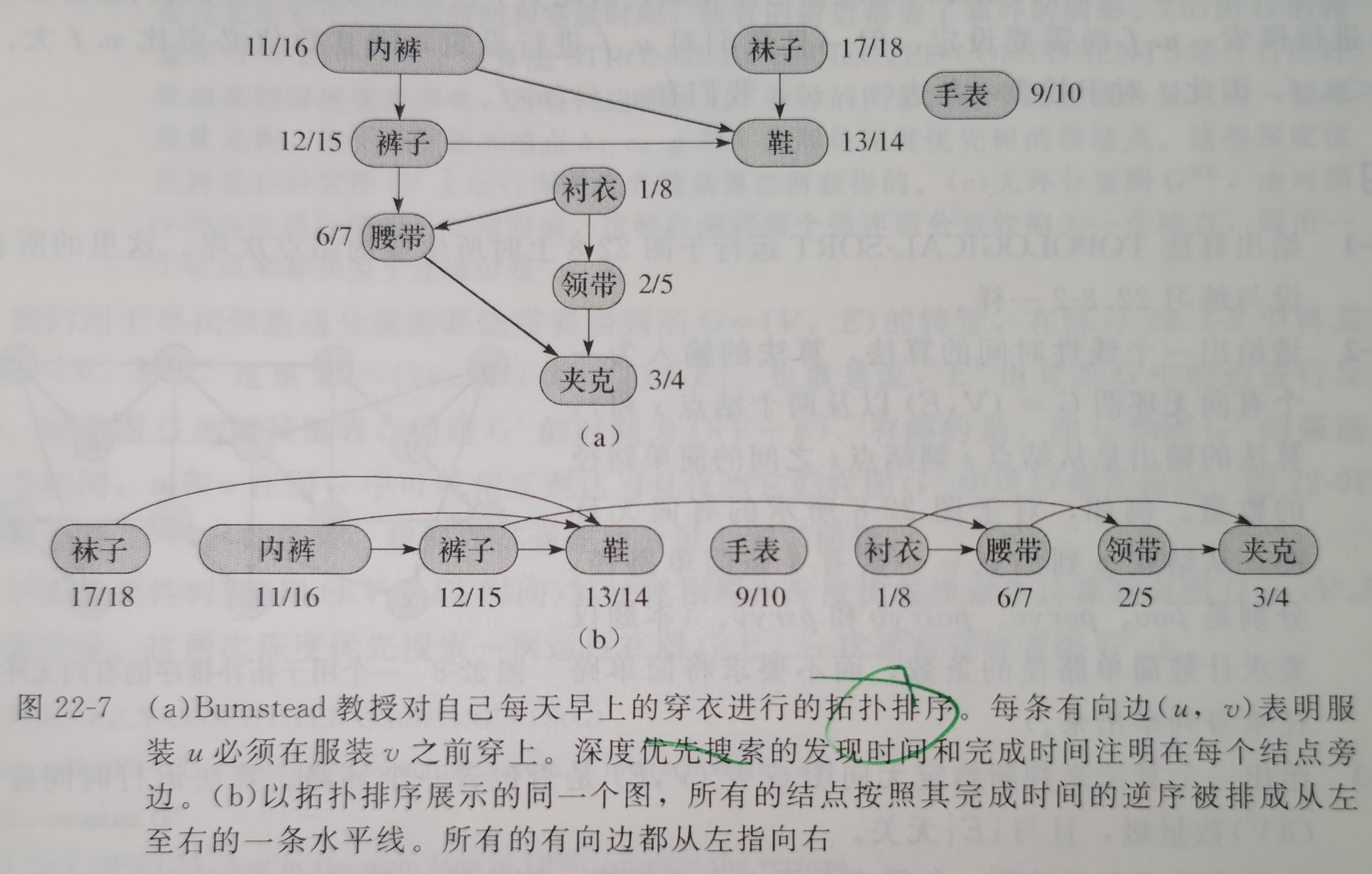
拓扑排序
用深度优先搜索来对有向无环图进行拓扑排序。
对于一个有向无环图\(G = (V, E)\)来说,其拓扑排序是\(G\)中所有结点的一种线性次序,该次序满足如下条件:如果图\(G\)包含边\((u, v)\),则结点\(u\)在拓扑排序中处于结点\(v\)的前面。可以将图的拓扑排序看做是将图的所有结点在一条水平线上排开,图的所有有向边都从左指向右。
下面的简单算法可以对一个有向无环图进行拓扑排序:
TOPOLOGICAL-SORT(G)
1 call DFS(G) to compute finishing times v.f for each vertex v
2 as each vertex is finished, insert it onto the front of a linked list
3 return the linked list of vertices
我们可以在\(\Theta(V + E)\)的时间内完成拓扑排序,因为深度优先搜索算法的运行时间为\(\Theta(V + E)\),将结点插入到链表最前端所需的时间为\(O(1)\),而一共只有\(|V|\)各结点需要插入。
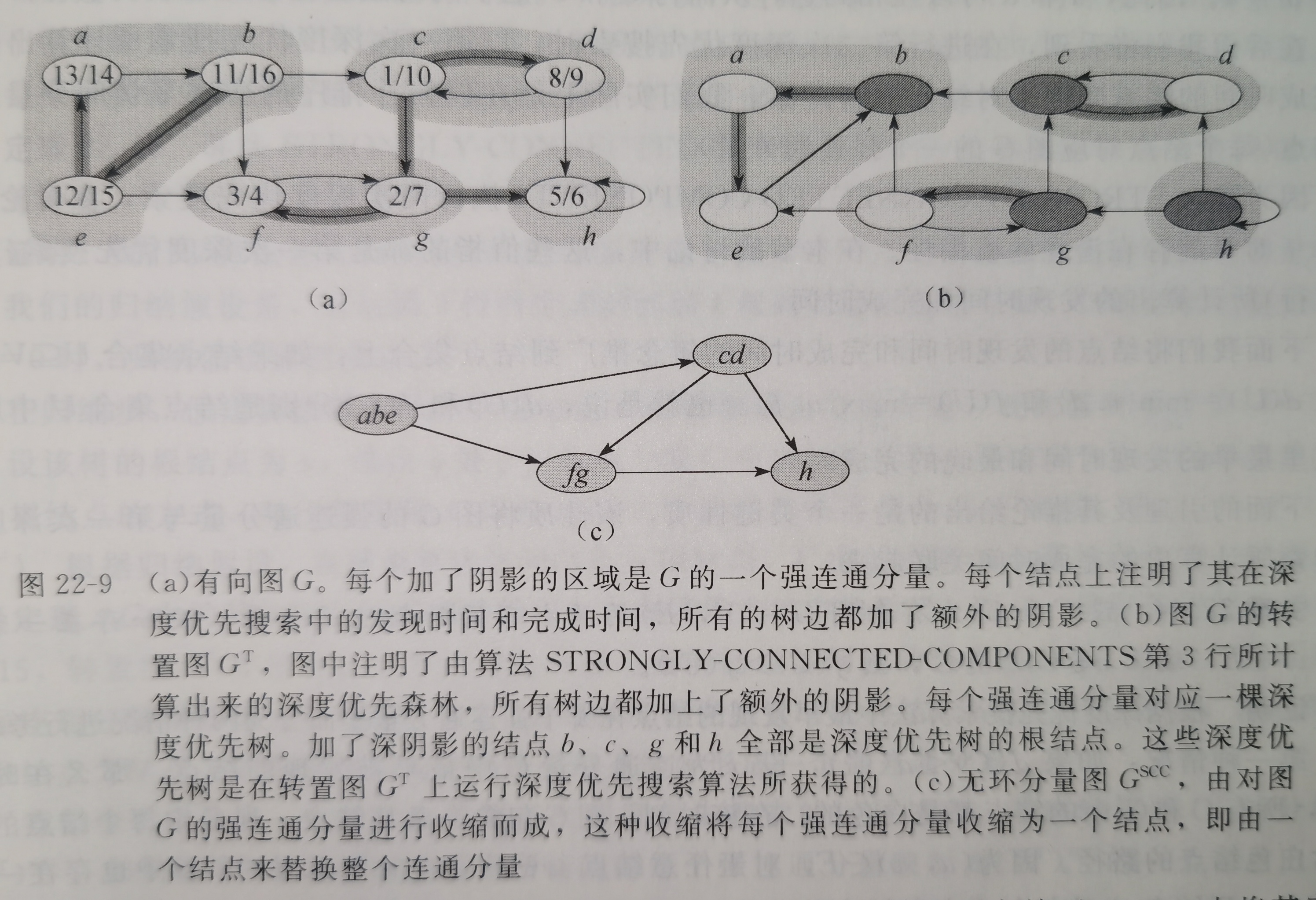
强连通分量
用深度优先搜索来将有向图分解为强连通分量。
有向图\(G = (V, E)\)的强连通分量是一个最大结点集合\(C \subset V\),对于该集合中的任意一对结点\(u\)和\(v\)来说,路径\(u->v\)和路径\(v->u\)同时存在;也就是说两结点可以互相到达。
因此引入有向图的转置:\(G^T = (V, E^T)\),其中\(E^T = \{(u, v):(v, u) \in E\}\),创建\(G^{T}\)的时间为\(O(V + E)\)。
图\(G\)和图\(G^T\)的强连通分量完全相同。
下面的\(\Theta(V + E)\)时间算法使用两次深度优先搜索来计算有向图\(G = (V, E)\)的强连通分量。两次分别运行在图\(G\)和图\(G^T\)上:
STRONGLY-CONNECTED-COMPONENTS(G)
1 call DFS(G^T) to compute finishing times u.f for each vertex u
2 compute G^T
3 call DFS(G), but in the main loop of DFS, consider the vertices in order of decreasing u.f (as computed in line 1)
4 output the vertices of each tree in the depth-first forest formed in line 3 as a separate strongly connected component
上述算法背后的思想来自于分量图\(G^{SCC} = (V^{SCC}, E^{SCC})\)的一个关键性质:假定图\(G\)由强连通分量\(C_1, …, C_k\)。结点集\(V^{SCC}\)为\(\{v_1, …, v_k\}\),对于图\(G\)的每个强连通分量\(C_i\)来说,该集合包含代表该分量的结点\(v_i\)。如果对于某个\(x \in C_i\)和\(y \in C_j\),图\(G\)包含一条有向边\((x, y)\),则边\((v_i, v_j) \in E^{SCC}\)。
通过收缩所有相邻结点都在同一个强连通分量中的边,剩下的图就是\(G^{SCC}\)。
分量图的关键性质就是:分量图是一个有向无环图。
许多针对有向图的算法都以将有向图分解为强连通分量的操作开始。在将图分解为强连通分量后,这些算法将分别运行在每个连通分量上,然后根据连通分量之间的连接结构将各个结果组合起来,从而获得最终所需的结果。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号