算法导论(第16章 贪心算法)
第16章 贪心算法
贪心算法(greedy algorithm)总是做出局部最优的选择,寄希望这样的选择能导致全局最优解。
贪心算法并不保证得到最优解,但对很多问题确实可以求得最优解。
后面的章节中会提出很多利用贪心策略设计的算法:
第23章 最小生成树
第24章 单源最短路径——Dijkstra算法
第35章 近似算法——Chvatal贪心启发式算法
16.1 活动选择问题
假定有一个n个活动(activity)的集合\(S\)=\({a_1, a_2, …, a_n}\),这些活动使用同一个资源,而这个资源在某个时刻只能供一个活动使用。每个活动\(a_i\)都有一个开始时间\(s_i\)和一个结束时间\(f_i\),其中\(0\leqslant s_i<f_i<∞\)。
- 如果被选中,任务\(a_i\)发生在半开时间区间[\(s_i\), \(f_i\))期间。
- 如果两个活动\(a_i\)和\(a_j\)满足[\(s_i\), \(f_i\))和[\(s_j\), \(f_j\))不重叠,则称它们是兼容的。也就是说,若\(s_i\geqslant f_j\)或\(s_j\geqslant f_i\),则\(a_i\)和\(a_j\)是兼容的。
在活动选择问题中,我们希望选出一个最大兼容活动集。
假定活动已按结束时间的单调递增顺序排序:
\(f_1\leqslant f_2\leqslant f_3\leqslant…\leqslant f_{n-1}\leqslant f_n\)
(稍后,我们会看到这一假设的好处)。
解决策略:
- 通过动态规划将这个问题分为两个子问题,然后将两个子问题的最优解整合成原问题的一个最优解。
- 贪心算法只需考虑一个选择,在做贪心选择时,子问题之一必是空的,只留下一个非空子问题。
我们将找到一种递归贪心算法来解决活动调度问题,并将递归算法转化为迭代算法,以完成贪心方法的过程。
活动选择问题的最优子结构
令\(S_{ij}\)表示在\(a_i\)结束之后开始,且在\(a_j\)开始之前结束的那些活动的集合。
假定\(A_{ij}\)是\(S_{ij}\)的一个最大的相互兼容的活动子集,包含活动\(a_k\)。因此我们得到两个子问题:寻找\(S_{ik}\)中的兼容活动以及寻找\(S_{kj}\)中的兼容活动。
令\(A_{ik}=A_{ij}∩S_{ik}\)和\(A_{kj}=A_{ij}∩S_{kj}\),所以有\(A_{ij}=A_{ik}∪\{a_k\}∪A_{kj}\)。也就是说,\(S_{ij}\)中最大兼容任务子集\(A_{ij}\)包含\(|A_{ij}|=|A_{ik}|+|A_{kj}|+1\)个活动。
如果用\(c[i, j]\)表示集合\(S_{ij}\)的最优解的大小,则可得递归式——\(c[i, j]=c[i, k]+c[k, j]+1\)
接下来我们可以设计一个带备忘机制的递归算法,或者使用自底向上法填写表项。
贪心选择
选择\(S\)中最早结束的活动,因为它剩下的资源可供它之后尽量多的活动使用。(如果\(S\)中最早结束的活动有多个,我们可以选择其中任意一个)
由于活动已按结束时间单调递增的顺序排序,贪心选择就是活动\(a_1\)。(选择最早结束的活动并不是本问题唯一的贪心选择方法,见练习16.1-3)
作出贪心选择后,只剩下一个子问题需要求解:寻找在\(a_1\)结束后开始的活动(即\(S_1\))。(最优子结构的性质告诉我们:如果\(a_1\)在最优解中,那么原问题的最优解由活动\(a_1\)及子问题\(S_1\)中所有活动组成)
所以,我们可以反复选择最早结束的活动,直至不再有剩余活动。而且,因为我们总是选择最早结束的活动,所以选择的活动的结束时间必然是严格递增的。我们只需按结束时间的单调递增顺序处理所有活动,每个活动只考查一次。
此时,我们只需自顶向下进行计算。
- 定理16.1 考虑任意非空子问题\(S_k\),令\(a_m\)是\(S_k\)中结束时间最早的活动,则\(a_m\)在\(S_k\)的某个最大兼容活动子集中。

递归贪心算法
设计一个直接的递归过程来实现贪心算法。
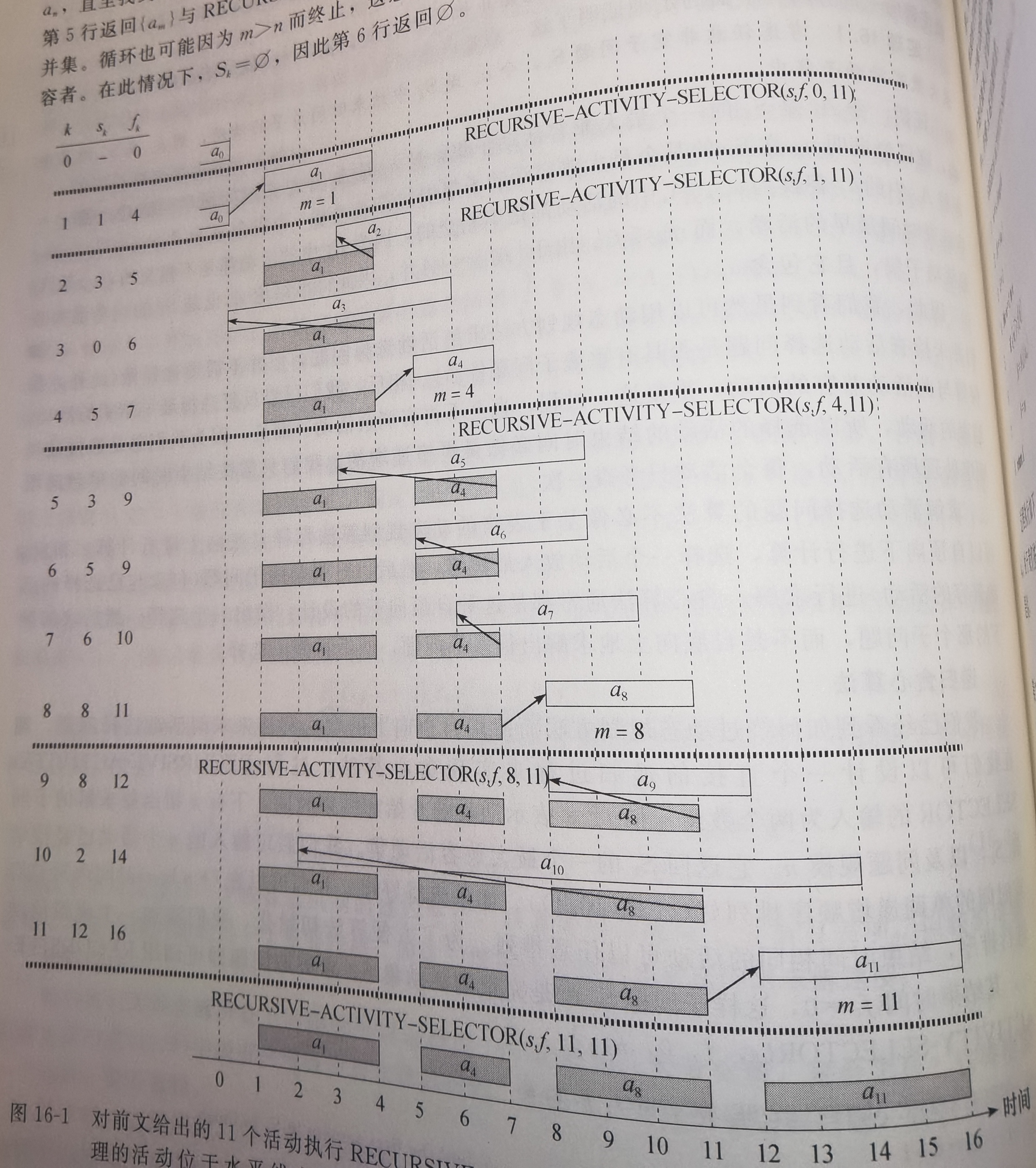
过程RECURSIVE-ACTIVITY-SELECTOR的输入为两个数组\(s\)和\(f\),表示活动的开始和结束时间,下标\(k\)指出要求解的子问题\(S_k\),以及问题规模\(n\)。它返回\(S_k\)的一个最大兼容活动集。
我们假定输入的\(n\)个活动已经按结束时间的单调递增顺序排列好。如果未排好序,我们可以在\(O(nlgn)\)时间内对它们进行排序,结束时间相同的活动可以任意排列。
为了方便算法初始化,我们添加一个虚拟活动\(a_0\),其结束时间\(f_0=0\),这样子问题\(S_0\)就是完整的活动集\(S\)。求解原问题即可调用RECURSIVE-ACTIVITY-SELECTOR(\(s, f, 0, n\))。
RECURSIVE-ACTIVITY-SELECTOR(s, f, k, n)
1 m = k + 1
2 while m ≤ n and s[m] ≥ f[k] // find the first activity to finish
3 m = m + 1
4 if m ≤ n
5 return {a_m} ∪ RECURSIVE-ACTIVITY-SELECTOR(s, f, m, n)
6 else return ∅
假定活动已经按结束时间排好序,则递归调用RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n)的运行时间为\(Θ(n)\)。
在整个递归调用过程中,每个活动被且只被while循环检查一次。特别地,活动\(a_i\)在\(k<i\)的最后一次调用中被检查。
迭代贪心算法
过程RECURSIVE-ACTIVITY-SELECTOR几乎就是“尾递归”:它以一个对自身的递归调用再解决一次并集操作结尾。
将一个尾递归过程改为迭代形式通常是很直接的:
GREEDY-ACTIVITY-SELECTOR(s, f)
1 n = s.length
2 A = {a_1}
3 k = 1
4 for m = 2 to n
5 if s[m] ≥ f[k]
6 A = A ∪ {a_m}
7 k = m
8 return A
与递归版本类似,在输入活动已按结束时间排序的前提下,GREEDY-ACTIVITY-SELECTOR的运行时间为\(Θ(n)\)。
总结
16.1节对于活动选择问题设计贪心算法的过程如下:
- 确定问题的最优子结构。
- 设计一个递归算法。
- 证明如果我们做出一个贪心选择,则只剩下一个子问题。
- 证明贪心选择总是安全的(步骤3、4的顺序可以调换)。
- 设计一个递归算法实现贪心策略。
- 将递归算法转换为迭代算法。
16.2 贪心算法原理
更一般地,我们可以按如下步骤设计贪心算法:
- 将最优化问题转化为这样的形式:对其做出一次选择后,只剩下一个子问题需要求解。
- 证明做出贪心选择后,原问题总是存在最优解,即贪心选择总是安全的。
- 证明做出贪心选择后,剩余的子问题满足性质:其最优解与贪心选择组合即可得到原问题的最优解,这样就得到了最优子结构。
每个贪心算法都对应一个更繁琐的动态规划算法。
证明一个最优化问题中贪心算法的可行性,贪心选择性质和最优子结构是两个关键要素。
贪心选择性质(greedy-choice property)
贪心选择性质:我们可以通过做出局部最优(贪心)选择来构造全局最优解。
在动态规划中,每个步骤都要进行一次选择,但选择通常依赖于子问题的解——自底向上的方式。(也可以自顶向下求解,但需要备忘机制。当然,即使算法是自顶向下进行计算,我们仍然需要先求解子问题再进行选择。)
在贪心算法中,总是做出当时看来最佳的选择,然后求解剩下的唯一的子问题——自顶向下的方式。
当然,必须证明每个步骤做出贪心选择能生成全局最优解。(证明步骤通常首先考查某个子问题的最优解,然后用贪心选择替换某个其他选择来修改此解,从而得到一个相似但更小的子问题。)
通过对输入进行预处理或者使用适合的数据结构(通常是优先队列),我们通常可以使贪心选择更快速,从而得到更高效的算法。(比如活动选择问题中将活动按结束时间单调递增顺序排序)
最优子结构(optimal substructure)
最优子结构性质:一个问题的最优解包含其子问题的最优解。——能否应用动态规划和贪心方法的关键要素。
当应用于贪心算法时,我们通常使用更为直接的最优子结构。我们假定,通过对原问题应用贪心选择即可得到子问题。只要证明:将子问题的最优解与贪心选择组合在一起就能生成原问题的最优解。(数学归纳法)
贪心对动态规划
二者都利用了最优子结构的性质。为了说明两种方法之间的细微差别,下面研究一个经典最优化问题的两个变形。
0-1背包问题(0-1 knapsack problem)
一个正在抢劫商店的小偷发现了\(n\)个商品,第\(i\)个商品价值\(v_i\)美元,重\(w_i\)磅,\(v_i\)和\(w_i\)都是整数。这个小偷希望拿走价值尽量高的商品,但他的背包最多能容纳\(W\)磅重的商品,\(W\)是一个整数。他应该拿哪些商品呢?(我们称这个问题是0-1背包问题,因为对每个商品,小偷要么把它完整拿走,要么把它留下;他不能只拿走一个商品的一部分,或者把一个商品拿走多次。)
分数背包问题(fractional knapsack problem)
设定与0-1背包问题是一样的,但对每个商品,小偷可以拿走其一部分,而不是只能做出二元(0-1)选择。(可以将0-1背包问题中的商品想象为金锭,分数背包问题中的商品想象为金砂)
分析
贪心策略可以求解分数背包问题,而不能求解0-1背包问题。
为了求解分数背包问题,我们首先计算每个商品的每磅价值\(v_i/w_i\)。遵循贪心策略,小偷首先尽量多地拿走每磅价值最高的商品。如果该商品已全部拿走而背包尚未满,他继续尽量多地拿走每磅价值第二高的商品,依此类推,直至达到重量上限\(W\)。\(O(nlogn)\)
为了求解0-1背包问题,我们只能使用动态规划。\(O(nW)\)——此处还有一个k-优化算法。




16.3 赫夫曼编码(Huffman Coding)
赫夫曼编码可以很有效地压缩数据:通常可以节省20%~90%的空间,具体压缩率依赖于数据的特性。我们将待压缩数据看做是字符序列。根据每个字符的出现频率,赫夫曼贪心算法构造出字符的最优二进制表示。
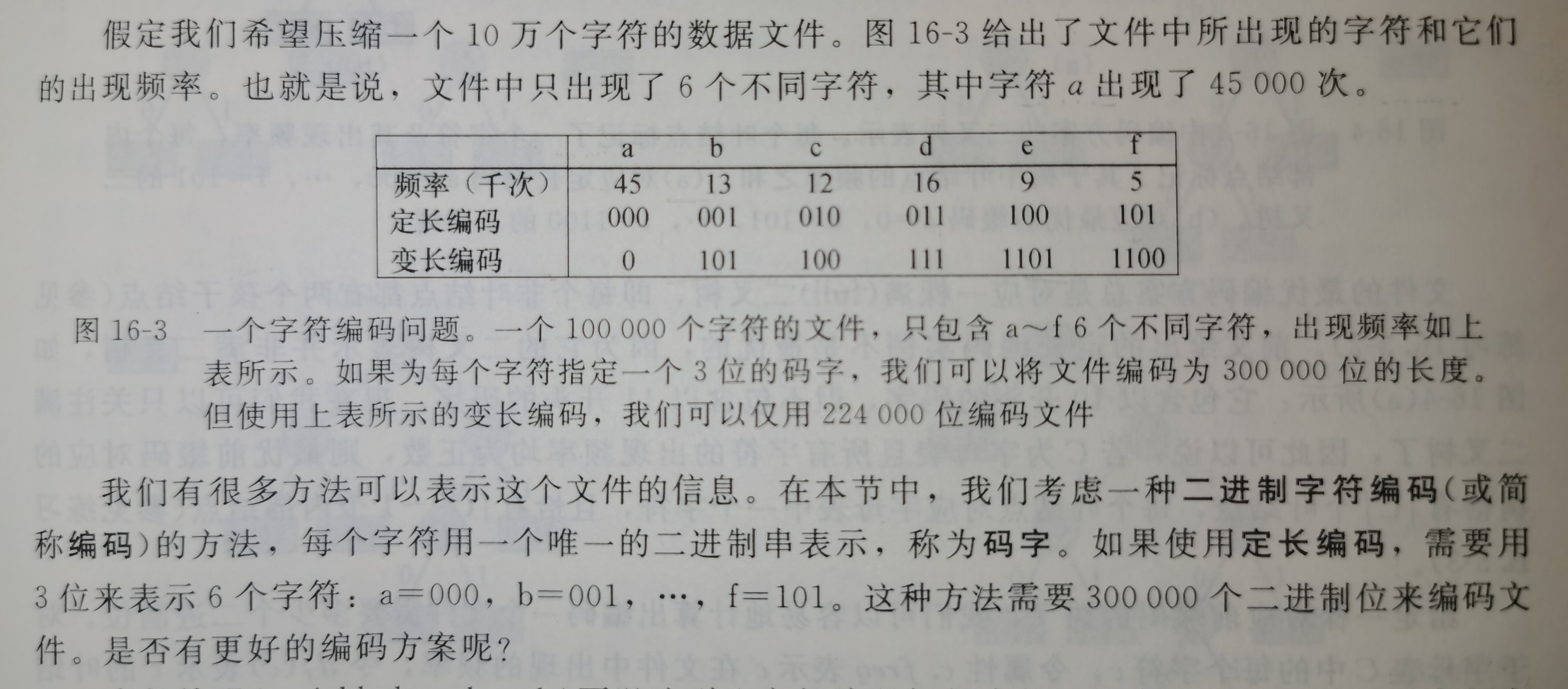
变长编码(variable-length code)可以达到比定长编码好得多的压缩率,其思想是赋予高频字符短码字,赋予低频字符长码字。
我们这里只考虑前缀码(prefix code)——没有任何码字是其它码字的前缀。(最优数据压缩率、简化解码过程)
我们构造一棵二叉树来表示前缀码,以便截取码字。其叶结点为给定的字符,字符的二进制码字用从根结点到该字符叶节点的简单路径表示,其中0意味着“转向左孩子”,1意味着“转向右孩子”。
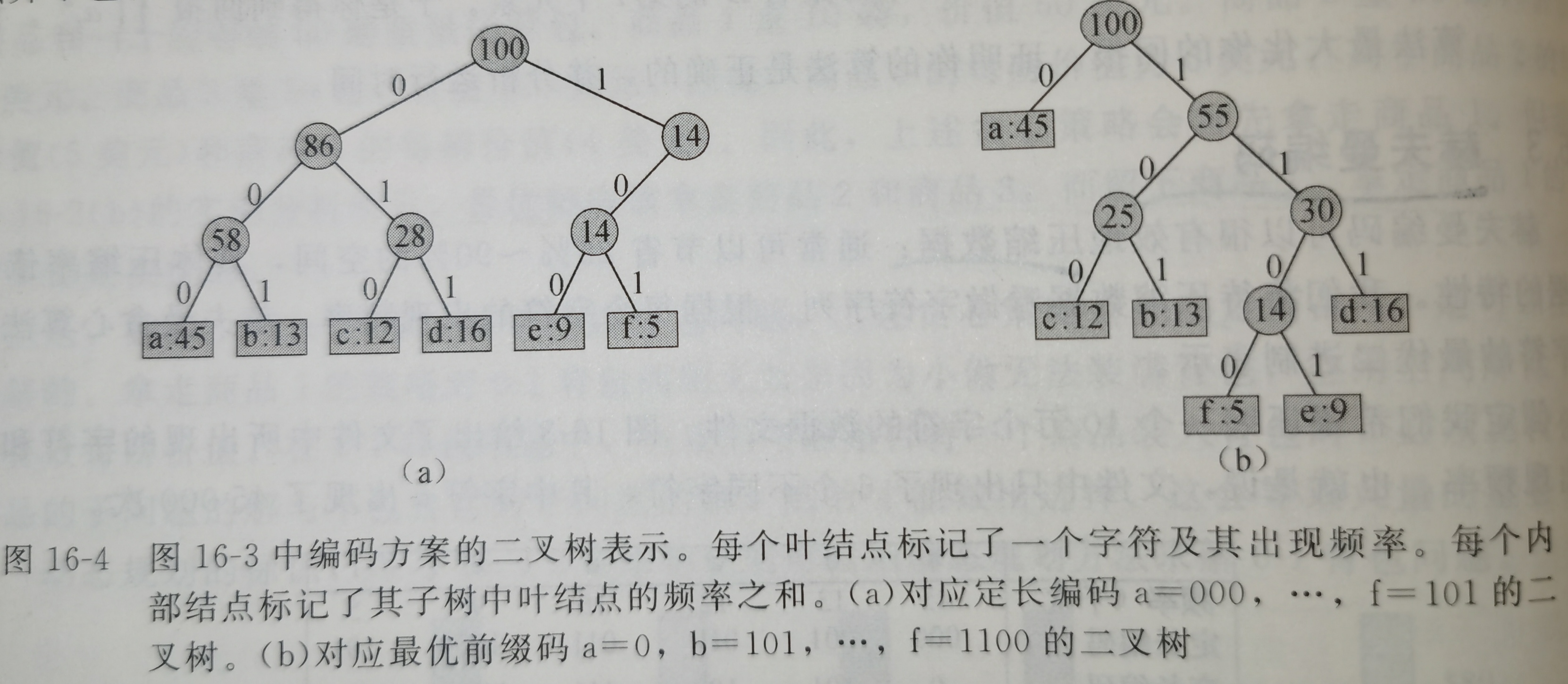
文件的最优编码方案总是对应一棵满(full)二叉树,即每个非叶结点都要两个孩子结点。
给定一棵对应前缀码的树T,我们可以容易地计算出编码一个文件需要多少个二进制位。对与字母表\(C\)中的每个字符\(c\),令属性\(c.freq\)表示\(c\)在文件中出现的频率,令\(d_T(c)\)表示\(c\)的叶结点在树中的深度。则编码文件需要\(B(T) = \sum_{c∈C}{c.freq·d_T(c)}\)个二进制位,我们将\(B(T)\)定义为\(T\)的代价。
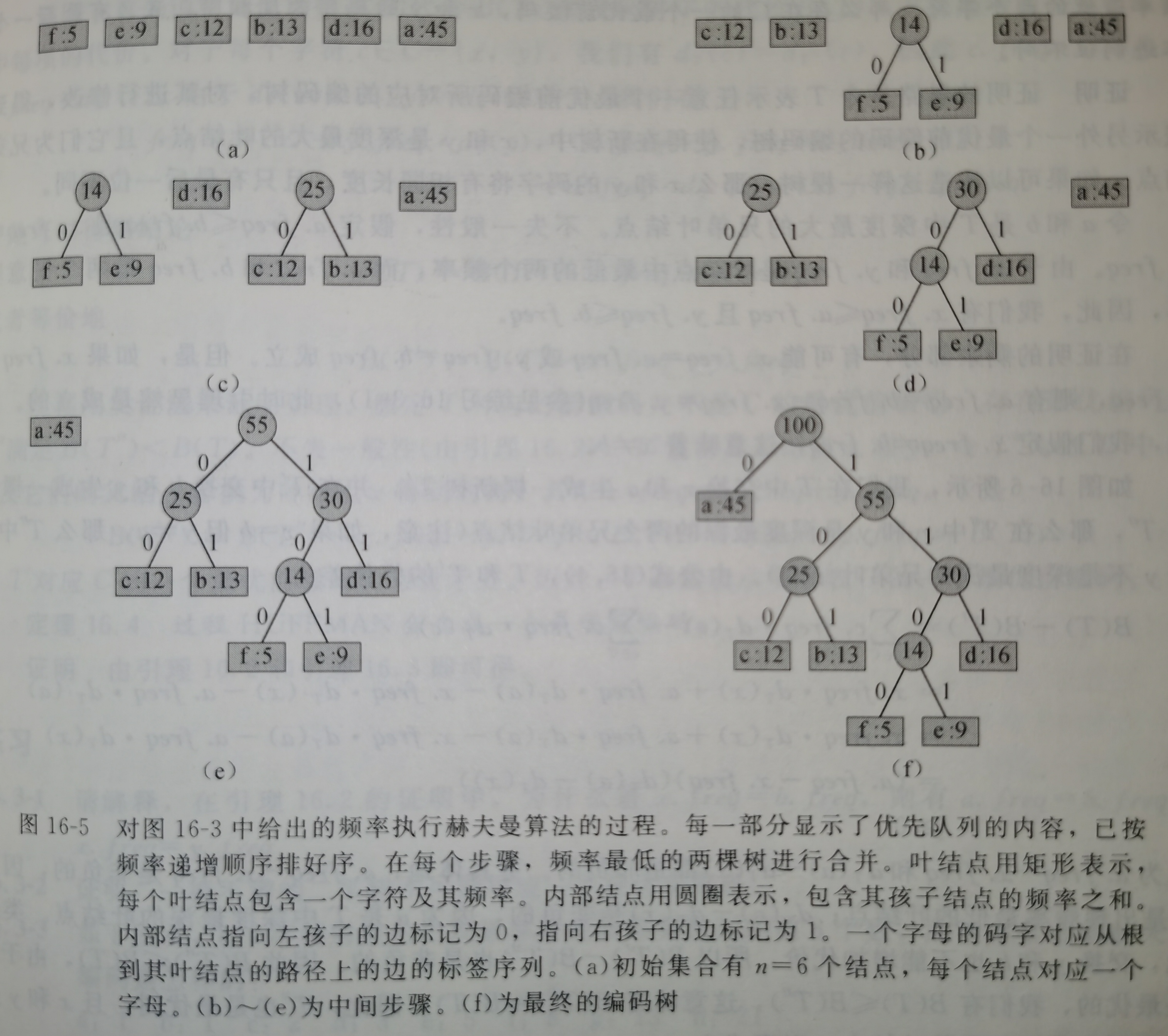
构造赫夫曼编码
在下面给出的伪代码中,我们假定\(C\)是一个n个字符的集合,而其中每个字符\(c∈C\)都是一个对象,其属性\(c.freq\)给出了字符的出现频率。算法自底向上地构造出对应最优编码的二叉树\(T\)。它从\(C\)个叶结点开始,执行\(|C| - 1\)个“合并”操作创建出最终的二叉树。算法使用一个以属性\(freq\)为关键字最小优先队列\(Q\),以识别两个最低频率的对象将其合并。当合并两个对象时,得到的新对象的频率设置为原来两个对象的频率之和。\(O(nlogn)\)(如果将最小二叉堆换为van Emde Boas树,可以将运行时间减少为\(O(nloglogn)\))
HUFFMAN(C)
1 n = |C|
2 Q = |C|
3 for i = 1 to n - 1
4 allocate a new node z
5 z.left = x = EXTRACT-MIN(Q)
6 z.right = y = EXTRACT-MIN(Q)
7 z.freq = x.freq + y.freq
8 INSERT(Q, z)
9 return EXTRACT-MIN(Q) //return the root of the tree
赫夫曼算法的正确性
下面的引理证明问题具有贪心选择性质。
- 引理16.2 令\(C\)为一个字母表,其中每个字符\(c∈C\)都有一个频率\(c.freq\)。令\(x\)和\(y\)是\(C\)中频率最低的两个字符。那么存在\(C\)的一个最优前缀码,\(x\)和\(y\)的码字长度相同,且只有最后一个二进制位不同。

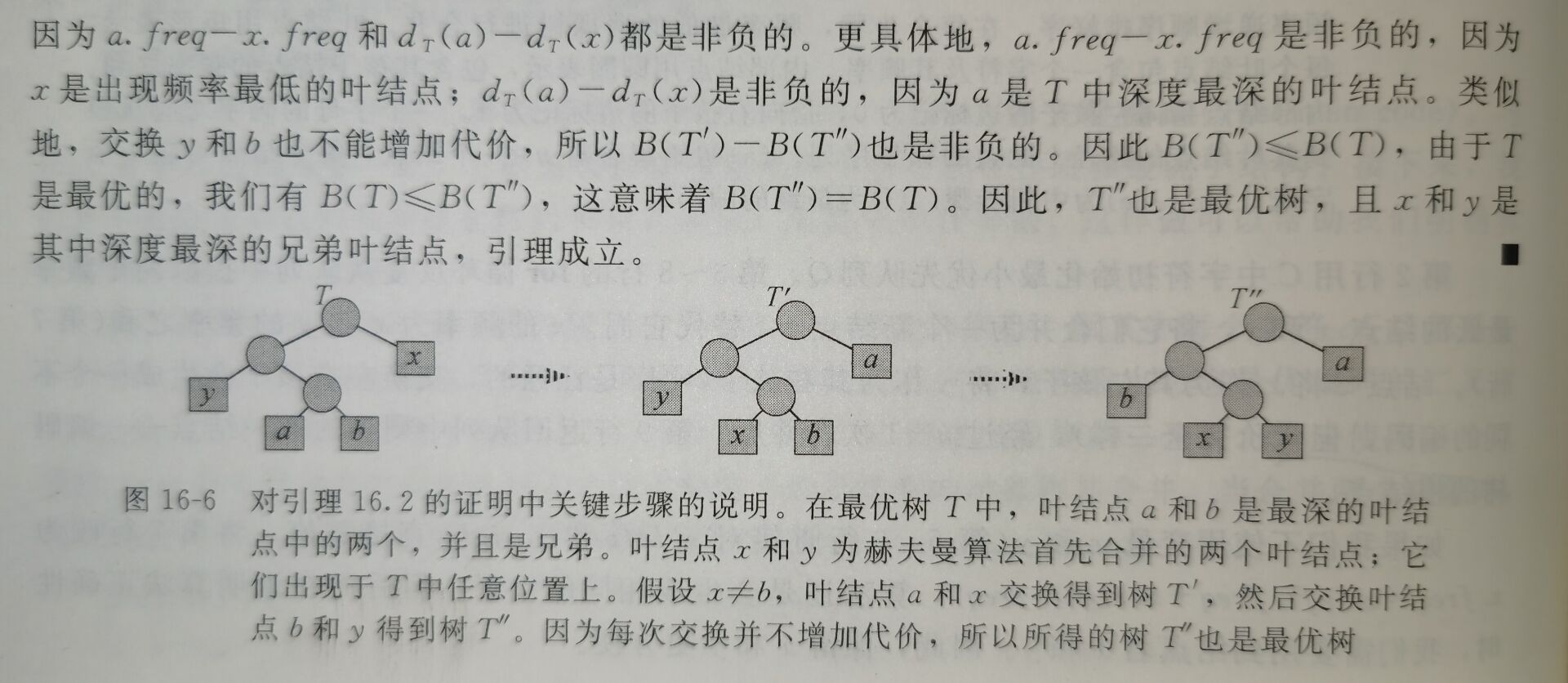
下面的引理证明问题具有最优子结构性质。
-

-

-
定理16.4 过程HUFFMAN会生成一个最优前缀码。
-
证明:由引理16.2和引理16.3即可得。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号