深入理解计算机系统（第2章 信息的表示和处理③）
目录
2.4 浮点数
2.4.1 二进制小数
我们套用十进制小数的定义
考虑一个形如\(b_{m}b_{m-1}…b_{1}b_{0}.b_{-1}b_{-2}…b_{n-1}b_{n}\)的二进制表示法。
用这种表示方法表示的二进制小数b定义如下：
\(b\) = \(\sum_{i=-n}^{m}2^i×b_{i}\)
2.4.2 IEEE（电气和电子工程师协会，读做“eye-triple-ee”）浮点表示
IEEE浮点标准用\(V\) = \((-1)^{s}×M×2^{E}\)的形式来表示一个数：
- 符号(sign)——s。
- 尾数(significand)——M，二进制小数，范围是1到2-\(ε\)，或者是0到1-\(ε\)。
- 阶码(exponent)——E，对浮点数加权，权重是2的E次幂（可能是负数）。
将浮点数的位表示划分为三个字段分别进行编码：
- 一个单独的符号位s直接编码符号s。
- k位的阶码字段exp = \(e_{k-1}…e_{1}e_{0}\)编码阶段E。
- n位小数字段frac = \(f_{n-1}…f_{1}f_{0}\)编码尾数M。（依赖阶码字段的值是否等于0）
给定位表示，根据exp的值，被编码的值可以分成三种不同的情况：
情况1：规格化的值
情况2：非规格化的值
逐渐下溢(gradual underflow)
情况3：特殊值
IEEE编码方式的特殊性质：
2.4.3 数字示例
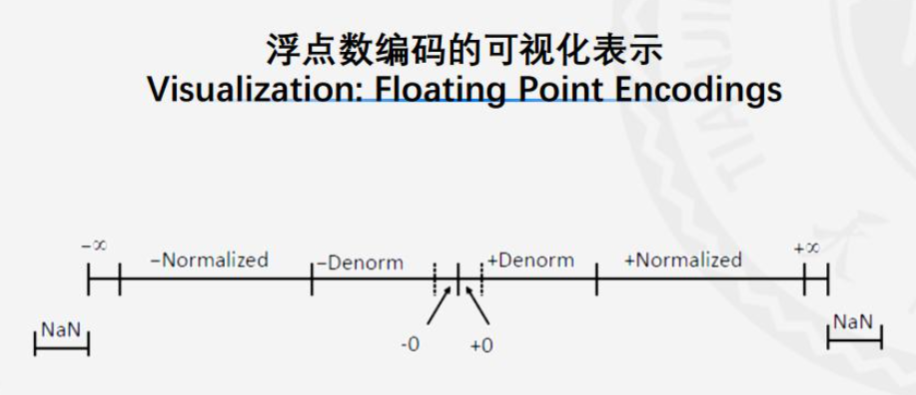
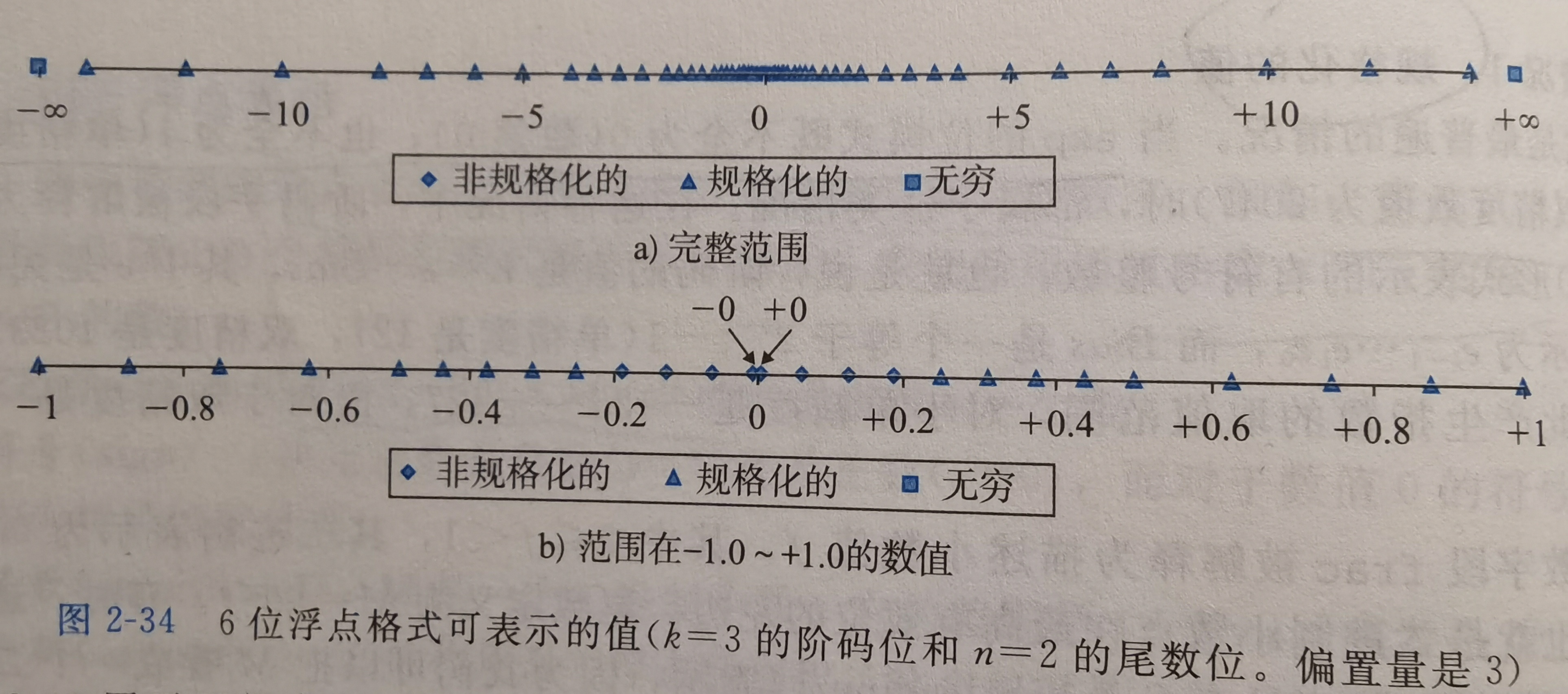
示例1：
- 特征：非规格化数是等间距的，规格化数的间距由小变大
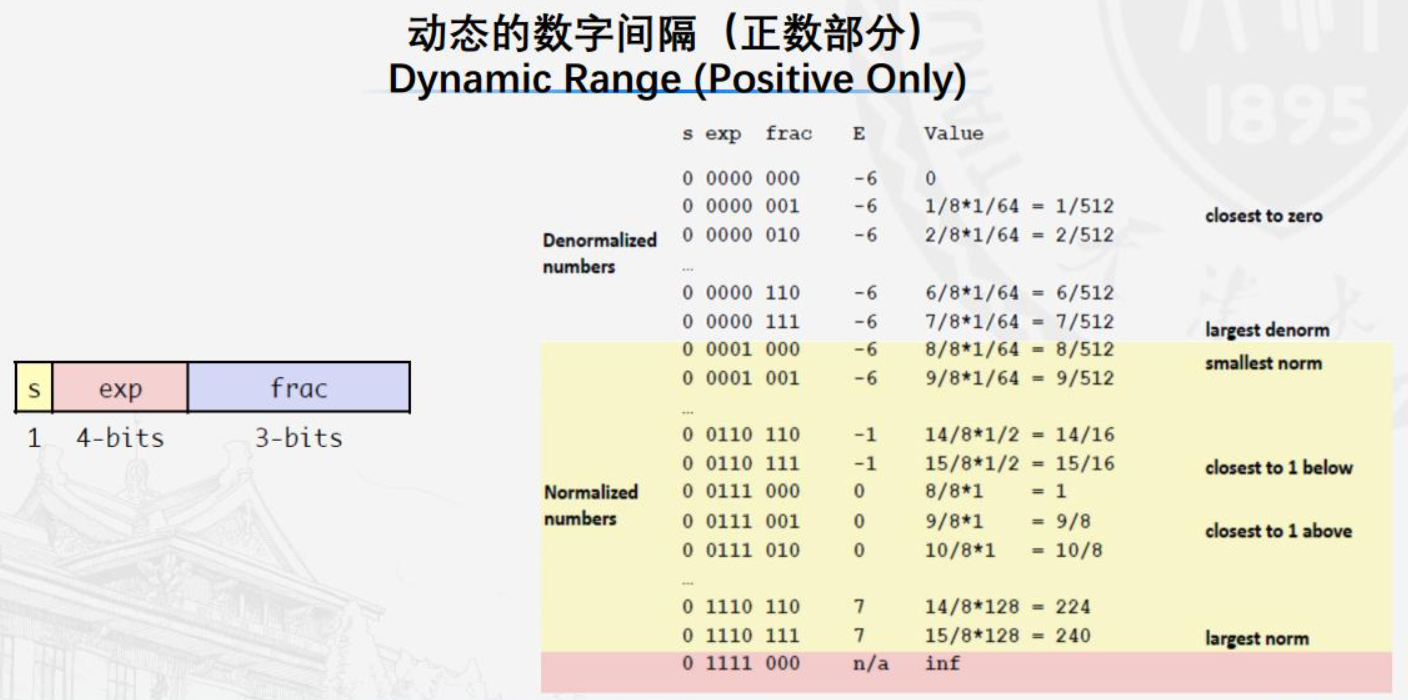
示例2：
2.4.4 舍入(rounding)
因为表示方法限制了浮点数的范围和精度，所以浮点运算只能近似地表示实数运算。需要通过舍入来找到最接近的匹配值。
舍入的四种方式：
- 向偶数舍入(round-to-even)/向最接近的值舍入(round-to-nearest)——浮点数运算默认的舍入模式一组正数的总和将始终被高估或者低估。（这里偶数的特征是二进制编码末位是0）
- 向零舍入
- 向下舍入
- 向上舍入
后三种方式产生实际值的确界(guaranteed bound)，且都会统计偏差。
2.4.5 浮点运算
- 加法
- 乘法
2.4.6 C语言中的浮点数
