CoPG
Paper2
Contrastive Policy Gradient: Aligning LLMs on sequence-level scores in a supervised-friendly fashion: https://arxiv.org/abs/2406.19185
Motivation
- 研究中经常使用强化学习中的基于偏好的奖励模型来对LLM进行微调。
- 关于上述任务,目前提出了各种直接对齐方法。
Challenge
- 直接对齐方法无法优化任意奖励,而且LLM并不只对基于偏好的奖励感兴趣。
- 基于普通策略梯度的强化学习微调开销较大,代价高昂。
Method
引入对比策略梯度(Contrastive Policy Gradient,CoPG)方法。该方法可以看作是一种不依赖重要性采样,并且强调使用正确状态基线重要性的离轨策略梯度方法。
-
对比方法不需要像RLHF那样对它们进行排序。对于一对独立的样本\(y\)和\(y^′\),引入以下样本损失:
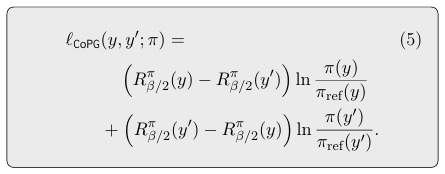
-
假设\(µ_1\)和\(µ_2\)是不需要通过分析得知的独立的分布(这与基于重要性采样的策略梯度方法相反),当然二者也可以是相同的。那么目标就可描述为最大化以下函数:
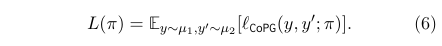
-
由于\(µ\)的期望奖励可以写成:
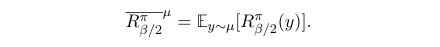
因此目标函数可以重写为(注意,在RL术语中,这并不是严格意义上的值,因为期望是在\(𝜇\)而不是\(𝜋\)之下。):
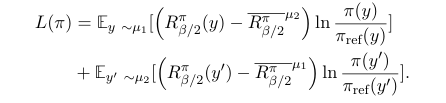
函数可以看作是一种加权对数似然,即在一种分布下加权对数似然的奖励与在另一种分布下的期望奖励的对比。这种损失是可监督的,因为它不涉及从训练好的策略中采样。
论文附录A详细证明了最大化目标函数\(𝐿\)能够解决预期问题。 -
对目标函数求梯度可以更明显地看出其与策略梯度的关系:

这在\(µ_1 = µ_2\)的情况下更为清晰:
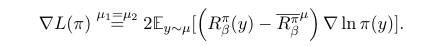
普通策略梯度:
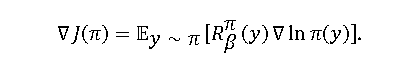
区别在于:- \(L(π)\)式中期望值不是根据学习到的政策\(π\)确定的,而是根据\(µ_1\)或\(µ_2\)确定的,这意味着它可以被理解为一个健全的离轨的策略梯度方法。
- \(L(π)\)式中有一个基线,即对比项,它是根据另一种分布(如果两者分布相同,则可以相同)得出的预期收益。最重要的是这个基线不能是任意的(因为一般来说\(E_{y∼µ}[∇lnπ(y)] \not= 0\)),它必须是一个特定的基线。
综上,策略梯度可以在使用正确基线的前提下安全地应用于离轨数据,而无需引入重要性采样修正项。
Algorithm
为了获得实用的算法,我们必须选择\(µ_1\)和\(µ_2\)是什么,它们是不同的还是相同的,以及如何估计期望值。所有这些选择都可能影响算法的稳定性和效率。(TODO)
这里作者专注于以离线方式从给定数据集中学习的简单情况,类似于现在常用的直接对齐方法,只不过CoPG不需要排名。

这是一个简单的、对监督友好的目标函数,可以通过对从数据集采样的小批量数据进行梯度上升来最小化。梯度可以通过自动微分得到:

Evaluation
论文在一个bandit问题上对提出的CoPG进行了实验,以说明其特性,并在一个总结任务上使用CoPG对LLM进行了微调,验证了该方法的有效性。
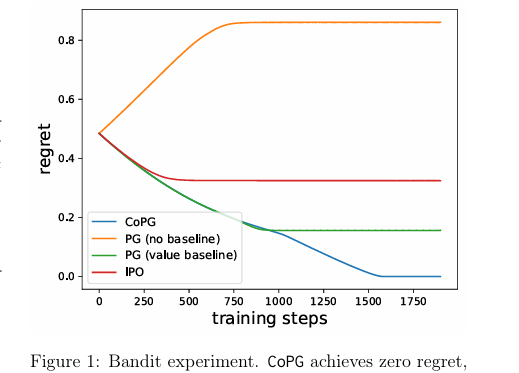
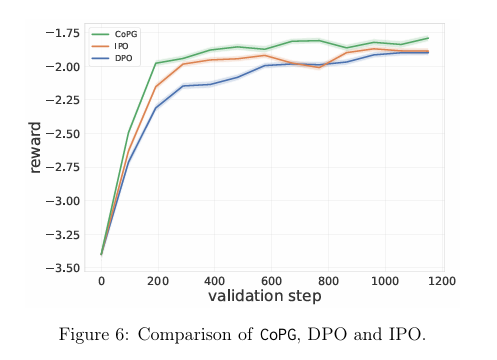
Conclusion
该文章提出了对比测量梯度方法,该方法能够以监督友好、开销较小、能够优化任意奖励的方式对LLM进行微调。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号