[POJ1195] Mobile phones(二维树状数组)
题目链接:http://poj.org/problem?id=1195
题意:四种操作:
0:初始化一个S*S的零矩阵
1:点(x,y)是值+A
2:查询一个子矩阵里所有数的和
3:退出
线段树由于不能在两棵树之间传递标记,所以这种求和的操作非常难处理。
改学了一下而为树状数组,发现可是比二维线段树简单多了。
记得之前曾经看过zkw线段树的ppt讲稿,好像zkw线段树的实现方法就是利用下标<<1和<<1|1可以构成一棵树而做的优化,所有对节点的操作跟树状数组极其相似,看来可以放弃普通树套树的二维线段树,而学用zkw线段树了。
这里二维树状数组update操作为从(0,0)到(x,y)这个子矩阵所有的值+val。
sum就是查询(0,0)到(x,y)这个子矩阵所有值的和。
对于本题,想要查询起点非(0,0)的子矩阵的和,只要和一维树状数组一样处理一下重叠部分就可以了,见下图:
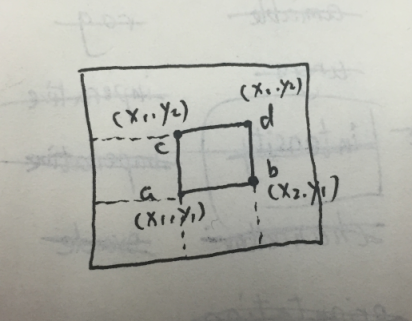
真的是太好写了。
1 #include <algorithm> 2 #include <iostream> 3 #include <iomanip> 4 #include <cstring> 5 #include <climits> 6 #include <complex> 7 #include <cassert> 8 #include <cstdio> 9 #include <bitset> 10 #include <vector> 11 #include <deque> 12 #include <queue> 13 #include <stack> 14 #include <ctime> 15 #include <set> 16 #include <map> 17 #include <cmath> 18 using namespace std; 19 20 const int maxn = 2020; 21 int n; 22 int bit[maxn][maxn]; 23 inline int lowbit(int x) { return x & (-x); } 24 25 void update(int i, int j, int val) { 26 for(int x = i; x <= n; x += lowbit(x)) { 27 for(int y = j; y <= n; y += lowbit(y)) { 28 bit[x][y] += val; 29 } 30 } 31 } 32 33 int sum(int i, int j) { 34 int ret = 0; 35 for(int x = i; x > 0; x -= lowbit(x)) { 36 for(int y = j; y > 0; y -= lowbit(y)) { 37 ret += bit[x][y]; 38 } 39 } 40 return ret; 41 } 42 43 int main() { 44 // freopen("in", "r", stdin); 45 int op; 46 int x1, y1, x2, y2, val; 47 scanf("%d%d",&op,&n); 48 memset(bit, 0, sizeof(bit)); 49 while(~scanf("%d", &op) && op != 3) { 50 if(op == 1) { 51 scanf("%d%d%d",&x1,&y1,&val); 52 x1++; y1++; 53 update(x1, y1, val); 54 } 55 else { 56 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 57 x1++; y1++; x2++; y2++; 58 int a = sum(x1-1, y1-1); 59 int b = sum(x2, y1-1); 60 int c = sum(x1-1, y2); 61 int d = sum(x2, y2); 62 printf("%d\n", a + d - c - b); 63 } 64 } 65 }
顺便祭奠一下写挂了的二维线段树:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define lrt rt << 1 5 #define rrt rt << 1 | 1 6 const int maxn = 1030; 7 8 9 typedef struct NodeY { 10 int val; 11 }NodeY; 12 13 typedef struct NodeX { 14 NodeY segY[maxn<<2]; 15 void build(int l, int r, int rt) { 16 segY[rt].val = 0; 17 if(l == r) return; 18 int mid = (l + r) >> 1; 19 build(l, mid, lrt); 20 build(mid+1, r, rrt); 21 } 22 23 void pushup(int rt) { 24 segY[rt].val = segY[lrt].val + segY[rrt].val; 25 } 26 27 void update(int p, int val, int l, int r, int rt) { 28 if(l == r) { 29 segY[rt].val += val; 30 return; 31 } 32 int mid = (l + r) >> 1; 33 if(p <= mid) update(p, val, l, mid, lrt); 34 else update(p, val, mid+1, r, rrt); 35 pushup(rt); 36 } 37 38 int query(int L, int R, int l, int r, int rt) { 39 if(L <= l && r <= R) return segY[rt].val; 40 int mid = (l + r) >> 1; 41 int ret = 0; 42 if(L <= mid) ret += query(L, R, l, mid, lrt); 43 if(mid < R) ret += query(L, R, mid+1, r, rrt); 44 return ret; 45 } 46 }NodeX; 47 48 NodeX segX[maxn<<2]; 49 int n; 50 51 void build(int l, int r, int rt) { 52 segX[rt].build(1, n, 1); 53 if(l == r) return; 54 int mid = (l + r) >> 1; 55 build(l, mid, lrt); 56 build(mid+1, r, rrt); 57 } 58 59 void update(int x, int y, int val, int l, int r, int rt) { 60 segX[rt].update(y, val, 1, n, 1); 61 if(l == r) return; 62 int mid = (l + r) >> 1; 63 if(x <= mid) update(x, y, val, l, mid, lrt); 64 else update(x, y, val, mid+1, r, rrt); 65 } 66 67 int query(int y1, int y2, int L, int R, int l, int r, int rt) { 68 if(L <= l && r <= R) return segX[rt].query(y1, y2, 1, n, 1); 69 int mid = (l + r) >> 1; 70 int ret = 0; 71 if(L <= mid) ret += query(y1, y2, L, R, l, mid, lrt); 72 if(mid < R) ret += query(y1, y2, L, R, mid+1, r, rrt); 73 return ret; 74 } 75 76 int main() { 77 freopen("in", "r", stdin); 78 int op, a, b, c, d; 79 scanf("%d %d", &op, &n); 80 build(1, n, 1); 81 while(~scanf("%d", &op) && op != 3) { 82 if(op == 1) { 83 scanf("%d%d%d",&a,&b,&c); 84 cout << a << " " << b << endl; 85 a++; b++; 86 update(a, b, c, 1, n, 1); 87 } 88 if(op == 2) { 89 scanf("%d%d%d%d",&a,&b,&c,&d); 90 a++; b++; c++; d++; 91 printf("%d\n", query(c, d, a, b, 1, n, 1)); 92 } 93 } 94 return 0; 95 }


