函数式编程

函数式编程介绍分为两章节。
第一章介绍C++函数式编程语法， 第二章简单介绍函数式编程思想。

C++语法

lambda表达式

lambda表达式是一个匿名函数。Lambda表达式基于数学中的λ演算得名，直接对应于其中的lambda抽象。

语法：[捕获列表](参数列表)->返回类型{函数体}

比如定义加法lambda表达式

// lambda表达式的类型是函数指针类型
int(*func)(int, int) = [](int x, int y) -> int {return x + y;};
// 省略返回类型
int(*func)(int, int) = [](int x, int y) {return x + y;};

• 捕获列表
  捕捉列表总是出现在lambda函数的开始位置，编译器根据[]来判断接下来的代码是否为lambda函数，捕捉列表能够捕捉上下文中的变量供lambda函数使用。不可省略。

  值	说明
  var	值传递方式捕捉变量var
  this	值传递方式捕捉this指针
  =	值传递方式捕获所有父作用域中的变量(包括this)
  &var	引用传递捕捉变量var
  &	引用传递捕捉所有父作用域中的变量(包括this)

  tips:
  值传递：形参是实参的拷贝，改变形参的值并不会影响外部实参的值。
  引用传递：指向实参地址，引用相当于实参的别名
  指针传递：有独立的地址，存储的值指向实参地址的指针
  

• 参数列表
  参数列表与普通函数的参数列表一致，如果不需要参数传递，可省略。

• 返回类型
  返回值类型。没有返回值时或返回值类型明确情况下，可省略。

• 函数体
  在该函数体内，除了可以使用其参数外，还可以使用所有捕获到的变量。不可省略。

类型推导

auto关键字

auto func = [](int x, int y) {return x + y;};

Function

类模版std::function是一种通用、多态的函数封装。std::function的实例可以对任何可以调用的目标实体进行存储、复制、和调用操作，这些目标实体包括普通函数、Lambda表达式、函数指针、以及其它函数对象等。

• 函数
• 函数指针
• lambda 表达式
• bind 创建的对象
• 重载函数调用运算符的类（仿函数）

#include <iostream>
#include <functional>

using namespace std;

int main() {
    function<int(int, int)> func = [](int x, int y){return x + y;};
    cout << func(5, 2) << endl;
    return 0;
}

函数式编程思想

λ演算

λ演算（lambda calculus）是一套从数学逻辑中发展，以变量绑定和替换的规则，来研究函数如何抽象化定义、函数如何被应用以及递归的形式系统。lambda演算作为一种广泛用途的计算模型，可以清晰地定义什么是一个可计算函数，而任何可计算函数都能以这种形式表达和求值。
λ演算可比拟是最根本的编程语言，它包括了一条变换规则（变量替换）和一条将函数抽象化定义的方式。

λ项

定义

语法	名称	描述
x	变量λ	用字符或字符串来表示参数或者数学上的值或者表示逻辑上的值
(λx.E)	抽象化	一个完整的函数定义（E是一个λ项），在表达式中的x都会绑定为变量x
(E1E2)	应用	将函数E1作用于参数E2,E1和E2是λ项

tips: λxy.xzy是λx.λy.xzy缩写形式

优先级

• E1E2形式
  表示函数调用，E1是函数，E2是参数；
  默认左结合，如 E1E2E3…En=(((E1E2)E3)…)En。

• λx.E形式
  表示函数抽象，x是形参，M是函数体；
  默认右结合，如 λx1⋅λx2⋅…λxn⋅E=λx1⋅(λx2⋅(…(λxn⋅E)…))

子表达式

设E是一个λ表达式, 那E的子表达式可以定义为

语法	子表达式
E≡x	x
E≡E1E2	E1、E2
E≡λx⋅E′	λx⋅E′、E′
E≡(E′)	E′的子表达式和E′

tips: SUB(E)表示E的所有子表达式

变量

作用域

对于λ表达式λx⋅E

• 定义点

  λx⋅即为定义点

• 作用域

  变量x为绑定变量，作用域为E中去掉所有形如λx⋅E′的子表达式的表达式部分

• 使用点

  在E中变量x的作用域出现的变量x

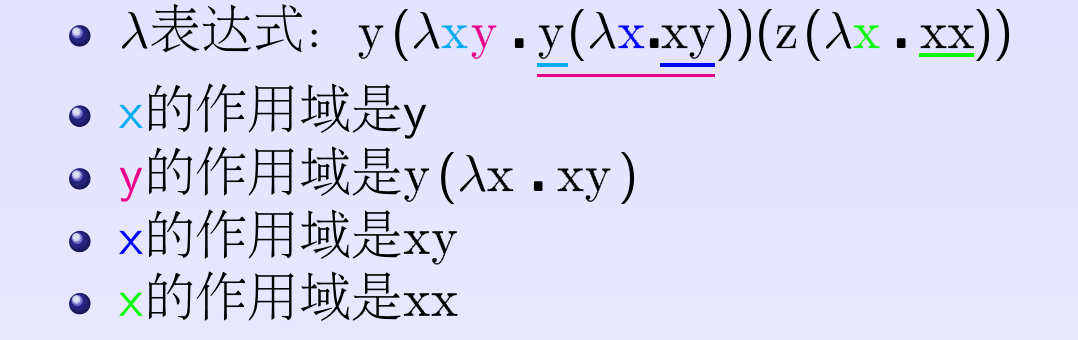
绑定变量及自由变量

绑定变量

bound variable，BV,lambda抽象中的变量.

语法	绑定关系	描述
x	BV(x) = ∅	变量是自由变量
(λx.M)	BV(λx.M) = BV(M) ∪	M抽象已有的绑定变量集合上新增变量x
(M N)	BV(MN) = BV(M) ∪ BV(N)	MN应用结果中的绑定变量集合是各自绑定变量集合的并集

自由变量

free variable，FV,非绑定变量的变量

语法	绑定关系	描述
x	FV(x) =	变量是自由变量
(λx.M)	FV(λx.M) = FV(M) -	M抽象已有的自由变量集合上减去变量x
(M N)	FV(MN) = FV(M) ∪ FV(N)	MN应用结果中的自由变量集合是各自自由变量集合的并集

约简

α变换

\[\lambda x \centerdot E \stackrel{\alpha}{\longrightarrow} \lambda y \centerdot(E[y/x]) \]

目的是改变绑定变量的名称，避免名称冲突。绑定的变量名称不重要。

对λ抽象进行α变换时，只能替换那些绑定到当前λ抽象上的变量。如 λ 抽象 λx.λx.x 可以 α 变换为 λx.λy.y 或 λy.λx.x，但是不能变换为 λy.λx.y。新的形参不允许是当前λ抽象自由变量 ，否则会改变当前λ抽象含义。

如果两个λ项可以通过α变换来进行转换，则这两个λ项是α等价的。比如

• \((\lambda x \centerdot \lambda x \centerdot x) \stackrel{\alpha}{\longrightarrow} (\lambda y \centerdot \lambda y \centerdot y)\)
• \((\lambda x \centerdot \lambda x \centerdot x) \stackrel{\alpha}{\longrightarrow} (\lambda x \centerdot \lambda y \centerdot y)\)
• \((\lambda x \centerdot ((\lambda y \centerdot yx) x)) \stackrel{\alpha}{\longrightarrow} (\lambda z \centerdot ((\lambda y \centerdot yz) z))\)

β约简

\[(\lambda x \centerdot E)E_0 \stackrel{\beta}{\longrightarrow} E[E_0/x] \]

β 约简（β-reduction）与函数应用相关。β约简用替换来表示函数应用。实际上定义了函数调用。

消解了λx.并在E中用λ项E0替代λ项x。比如

• \((\lambda x \centerdot xy) x \stackrel{\beta}{\longrightarrow} xy\)
• \((\lambda x \centerdot xx) y \stackrel{\beta}{\longrightarrow} yy\)

η变换

\[(\lambda x \centerdot Mx) \stackrel{\eta}{\longrightarrow} M \]

描述函数的外延等价性。外延性指的是如果两个函数当且仅当对所有参数的结果相同时，才被认为是相等的。比如

• \(\lambda x \centerdot (\lambda y \centerdot yy) x \stackrel{\eta}{\longrightarrow}(\lambda y \centerdot yy)\)

闭包

闭包是支持头等函数的编程语言中实现词法绑定的一种技术。

实现上是一个结构体，它存储了一个函数（通常是其入口地址）和一个关联的环境（相当于一个符号查找表）。环境里是若干对符号和值的对应关系，它既要包括约束变量，也要包括自由变量。有些函数也可能没有自由变量，即只有 函数指针。

闭包跟函数最大的不同在于，当捕捉闭包的时候，它的自由变量会在捕捉时被确定，这样即便脱离了捕捉时的上下文，它也能照常运行。捕捉时对于值的处理可以是值拷贝，也可以是名称引用。

#include <iostream>
#include <functional>

using namespace std;

int main() {
    function<function<int(int)>(int)> func = [](int x){return [x](int y) {return x + y;};};
    function<int(int)> addTwoFunc = func(2);
    cout << addTwoFunc(3) << endl; // 5
    cout << addTwoFunc(4) << endl; // 6
    return 0;
}

高阶函数

可以返回函数的函数

惰性求值

柯里化

把接受多个参数的函数变换成接受一个单一参数(最初函数的第一个参数)的函数，并且返回接受余下的参数且返回结果的新函数的技术。

public class CurryFunctions {
    // 未柯里化
    public static Integer sum(int t, int u, int v) {
        return t + u + v;
    }
    // 柯里化
    static  Function<Integer, Function<Integer, Function<Integer, Integer>>> sumCurry() {
        return t -> u -> v -> t + u + v;
    }

    public static void main(String[] args) {
        Function<Integer, Function<Integer, Function<Integer, Integer>>> sumCurry =  sumCurry();
        Function<Integer, Function<Integer, Integer>> addOne = sumCurry.apply(1);
        Function<Integer, Integer> addOneTwo = addOne.apply(2);

        System.out.println(addOne.apply(2).apply(3));
        System.out.println(addOneTwo.apply(3)); // 6
        System.out.println(addOneTwo.apply(4)); // 7
    }
}

函数组合

表驱动

#include <iostream>
#include <map>
#include <functional>

using namespace std;

int main() {

    using f = int(int, int);

    map<char, function<f>> f_map = {
        {'+', [](int x, int y){return x + y;}},
        {'-', [](int x, int y){return x - y;}},
        {'*', [](int x, int y){return x * y;}},
        {'/', [](int x, int y){return x / y;}}
    };

    cout << f_map['+'](5, 2) << endl;
    cout << f_map['-'](5, 2) << endl;
    cout << f_map['*'](5, 2) << endl;
    cout << f_map['/'](5, 2) << endl;

    return 0;
}

纯函数

透明性。同样的输入一定会是同样的输出，且不引起变化。