链表双指针技巧

题目	难度	要点
分隔链表	●	快慢指针:不用两个新链表拼接，使用原地修改
合并K个升序链表	●	最小堆:类ProirityQueue的使用
环形链表	●	快慢指针:相遇有环
环形链表II	●	快慢指针:入环第一个节点

分隔链表

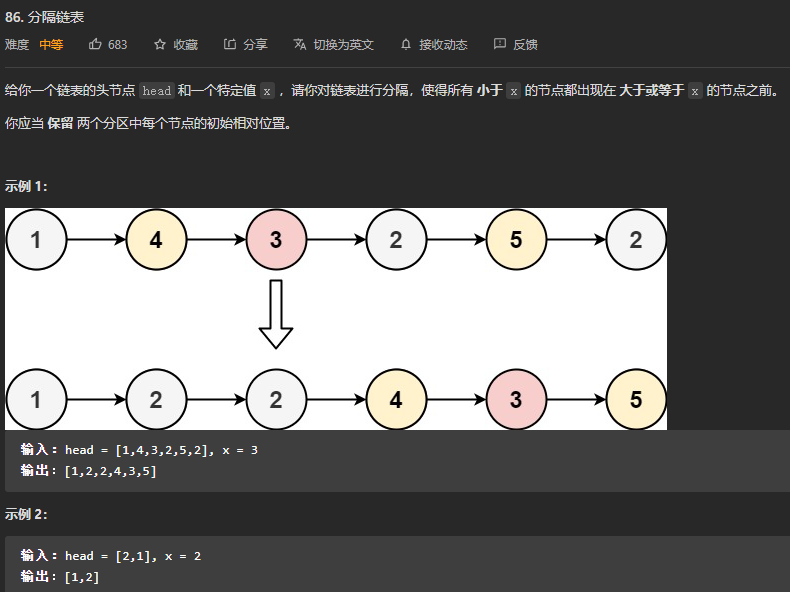
题目要求按原顺序，以x值将小的放链表前半段，其他的放链表后半段。很容易想到一种解法，新开两条链表分别存放，最后将两条链表合并。题目难度给个中等，可以考虑换个复杂点的原地修改解法。那么需要了解2个地方的信息：1.待插入的节点 2.需要移动的节点。很容易就可以想到快慢指针，慢指针等待插入，快指针寻找小于x的节点，进行操作即可。

public ListNode partition(ListNode head, int x) {
        ListNode dummy = new ListNode(-1, head);
        ListNode slow = dummy;
        while (slow.next != null && slow.next.val < x) {
            slow = slow.next;
        }
        ListNode fast = slow;
        while (fast != null && fast.next != null) {
            if (fast.next.val < x) {
                ListNode temp = fast.next;
                fast.next = temp.next;
                temp.next = slow.next;
                slow.next = temp;
                slow = slow.next;
            } else {
                fast = fast.next;
            }
        }
        return dummy.next;
    }

合并K个升序链表

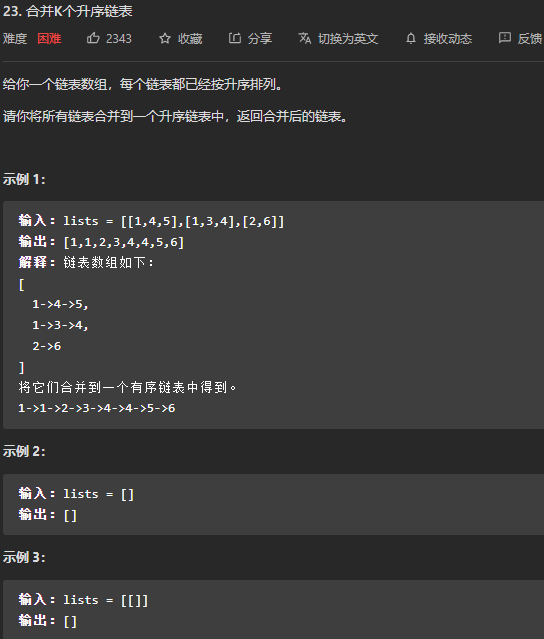
两个链表合并的升级版。JAVA没有大小堆的直接类，但是优先级队列类底层默认为最小堆，可指定Comparator变为最大堆。
思路：首先放链表个数的节点到最小堆中，每次取出最小的置于新链表。如果节点有子节点则加入优先级队列自动排序。重复步骤直到队列为空即可。

    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }
        ListNode dummy = new ListNode(), p = dummy;
        PriorityQueue<ListNode> pq = new PriorityQueue<>(lists.length, (a, b) -> (a.val - b.val));
        for (ListNode node: lists) {
            if (node != null) {
                pq.add(node);
            }
        }
        while (!pq.isEmpty()) {
            ListNode node = pq.poll();
            if (node.next != null) {
                pq.add(node.next);
            }
            p.next = node;
            p = p.next;
        }
        return dummy.next;
    }

环形链表

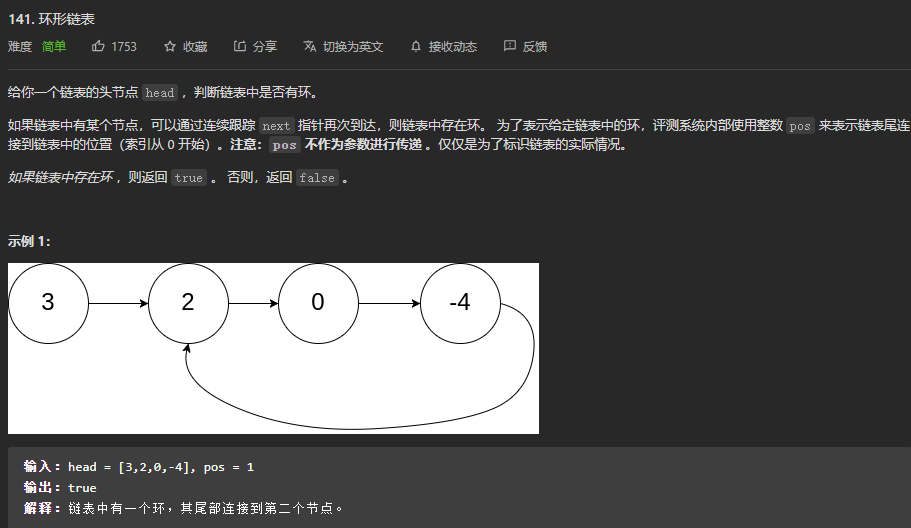
快慢指针经典题，两个指针相遇即有环，否则无环。

    public boolean hasCycle(ListNode head) {
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                return true;
            }
        }
        return false;
    }

环形链表II

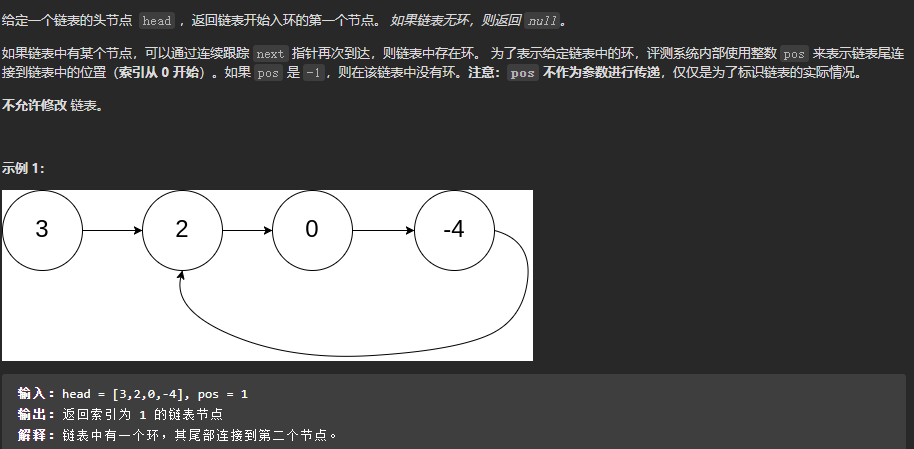
环形链表升级，返回入环的第一个节点。借用截图中例子，任意假设0节点相遇，那么此时slow跑了长度n，fast跑了长度2n。假设2节点到0节点长度为k，那么通过slow可得3节点到2节点长度为n-k，通过fast（fast比slow多跑了一个圈）可得-4节点到2节点长度为2n-n-k=n-k。那么slow或fast重置为head，都单步前进直到相遇即答案。

    public ListNode detectCycle(ListNode head) {
        ListNode slow = head, fast = head;
        // 判断是否有环
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                break;
            }
        }
        if (fast == null || fast.next == null) {
            return null;
        }
        // 寻找入环第一个节点
        slow = head;
        while (slow != fast) {
            slow = slow.next;
            fast = fast.next;
        }
        return slow;
    }

··