并查集

并查集是一种树型数据结构，主要用于处理不相交集合之间的合并和判断某一元素所在的集合（并查集中集体是用其最高父结点表示），这种数据结构维护一个数组，father[],用于记录每个元素的父亲，也就其所在的集合；其主要的操作有两种，查找和合并，查找是为了判断出指定元素所有的集合（树），对于查找算法可以用路径压缩进行优化；合并则是将两个不相交集合按某种标准进行合并成一个新的集合（树）；除了这两种主要的操作，并查集还有一个初始化的算法，主要是用于把每个元素都初始化单个元素的集合，也就是其father就是它本身；

相关的代码如下：

int father[MAX];

int rank[MAX];
//initialize every point as a set. And they are disjoin.
void Make_Set(int x) {
    father[x] = x;
    rank[x] = 0;
}

int Find_Set(int x) {
    //没有进行路径压缩的查找; 
    /*return x == father[x] ? father[x] : Find_set(father[x]);*/
    //进行了路径压缩的查找，对应的当调用该函数时,一般为x = Find_Set(x)
    if(x != father[x]) {
        father[x] = Find_set(father[x]);
    }
    return father[x];
}
//按秩将两个不相交的集合（也就是其根不相同， find_set不同）行合并；
int Union_Set(int x, int y) {
    x = Find_set(x);
    y = Find_set(y);
    
    if(x == y) {
        return;
    }
    if(rank[x] > rank[y]) {
        father[y] = x;
    }
    else {
        if(rank[x] == rank[y]) {
            ++rank[y];
        }
        father[x] = y;
    }
}

这里解释下什么叫做路径压缩？路径压缩是为了把查找的O(n)的代码降至O(1)， 从直观上来看就是希望让树的结构变成高度为2的多叉树；算法思想是要进行查找时，把没有直接连在根的结点用递归的方式连到根部，这样当再次进行查找本树时，其查找的消耗就为O(1)了，如图：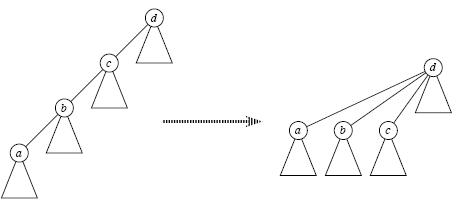

合并时，要记住要有一个的合并规则，根据什么标准进行合并，主要是考虑到哪一个根做为合并后的新根，同时记得要更新新树的标准；

关于并查集可以做下poj里的三个题目：poj_1611, poj_2524, poj_1861;

这里附上poj_1611的代码并说明：

#include<stdio.h>

int father[30003], num[30003];

void make_set(int n) {
    int i;
    for(i = 0; i < n; ++i)
        father[i] = i;
}

int find_set(int x) {
    /*return x == father[x] ? father[x] : find_set(father[x]);*/
    //路径压缩优化    
    if(x != father[x]) {
        father[x] = find_set(father[x]);
    }
    return father[x];
    
}

void union_set(int x, int y) {
    x = find_set(x);
    y = find_set(y);
    //care the union_rule
    if(x != y) {
        father[y] = x;   //这个是与外部相关的，main中的主要是用每个组的第一个集合的根做为合并后新树的根。
        num[x] += num[y];
    }
}


int main() {
    int n, m, t, i, x, y;
    while(scanf("%d%d", &n, &t), n+t) {
        make_set(n);
        for(i = 0; i < n; ++i)
            num[i] = 1;
        while(t--) {
            scanf("%d", &m);
            --m;
            scanf("%d", &x);
            while(m--) {
                scanf("%d", &y);
                union_set(x, y);
            }
        }

        printf("%d\n", num[find_set(0)]);
    }
}

并查集还且个极好的用法就是用来完成最小生成树的Kruskal算法，可以很方便的用于判断是否成环，如果两个点已经在同一个集合中了，则表明加入这两个点后将成环：另外合并的规则主要是看谁的集合中元素个数多；代码如下：

#include<iostream>
#include<algorithm>
#define MAX 100

using std::endl;
using std::cout;
using std::cin;


int parent[MAX];
int child[MAX];

struct Edge {
    int start, end;
    int weight;
};

bool comp(Edge a, Edge b) {
    return a.weight < b.weight;
}

int find(int child) {
    //return child == parent[child] ? child : find(parent[child]);
    //path_tar（outside child = find(child)）
    if(child != father[child] {
        father[child] = find(father[x]);
    }
    return father[x];
}

bool join(int first, int second) {
    int root1, root2;

    root1 = find(first);
    root2 = find(second);

    if(root1 == root2)
        return false;
    else {
        if(child[root1] >= child[root2]){
            parent[root2]  = root1;
            child[root1] += child[root2];
        }
           else {
            parent[root1] = root2;
            child[root2] += child[root1];
        }
    }
    return true;
}
int main() {
    int vertex_num, edge_num, i, sum, total;
       cin >> vertex_num >> edge_num;
    Edge edge[edge_num + 1]; // edge[0] is not used
    //init
    for(i = 0; i < vertex_num; ++i) {
        parent[i] = i;
        child[i] = 1;
    }
    for(i = 1; i <= edge_num; ++i) {
        cin >> edge[i].start >> edge[i].end >> edge[i].weight;}    
    std::sort(edge + 1, edge + 1 + edge_num, comp);

    for(sum = 0, total = 0, i = 1; i <= edge_num; ++i) {
        if(join(edge[i].start, edge[i].end)) {
            sum += edge[i].weight;
            ++total;
            cout << "Add the edge: " << edge[i].start << " -> " << edge[i].end << " : "<< edge[i].weight << endl;
        }
        if(total == vertex_num - 1)
        break;
    }
    cout << "The sum of the mst is " << sum << endl;
}

相关参与网站：http://blog.csdn.net/freezhanacmore/article/details/8629871
　　　　　　　http://zh.wikipedia.org/wiki/%E5%B9%B6%E6%9F%A5%E9%9B%86