【雷达原理】脉冲压缩-匹配滤波的自己理解与参考资料
在一般雷达走-停模型中,在慢时间停下的时候,做的是快时间的脉冲压缩。
(20.12.12)
先来说一下我自己的总结。
本部分为原创,转载请贴链接:https://www.cnblogs.com/kinologic/p/14105907.html
【第一个问题:为什么要脉冲压缩?】
一、距离分辨率
一个周期的脉冲信号,可以认为两部分
一个是有脉冲值的部分,我们记作是\(\tau\),一个是脉冲开始到下一个脉冲开始的时间,我们记作是\(T\),周期
很容易可以想到,将两个脉冲时间分开来的这个分辨力 就是\(\tau\)
因为两个有值的脉冲在一起的时候,会重叠吧,就不能分辨开了
我们就可以近似得到一个结论
雷达的分辨力是跟这个\(\tau\)成正比的
分辨力 \(\delta\propto\tau\)
而分辨力这个东西需要注意,它是越小越好的,谁都希望分辨力高对吧.
所以为了得到良好的距离分辨力,必须使用短脉冲,或者经过信号处理能够得到短脉冲的信号。
在雷达系统中,距离向分辨力\(\delta_r=\frac{c}{2B}\)
这个B是什么呢,是雷达发射信号的带宽
带宽又是什么呢?带宽就是在频带上占了多少,可以理解为频率f的变化范围
这个带宽,在脉冲信号上可以近似认为等于脉冲时常的倒数,因为\(\tau\)的选择是sinc函数下降为峰值4dB位置的宽度,这个宽度近似等于\(\frac{1}{B}\)
\(B=\frac{1}{\tau}\)
具体可以参考后面的资料。
二、为了得到精确的目标参数,接收信号的SNR必须高,需要提高平均发射功率,提高SNR有两个方式:
1.增大峰值功率(难以实现)
2.增加脉冲长度(通常使用)
为了实现一和二,使用了一个两全其美的方式:脉冲压缩。
具体如下:
发送一个展宽脉冲,再对其进行脉冲压缩,得到所需的分辨率。
【第二个问题:如何进行脉冲压缩?】
如何将回收的展宽脉冲进行压缩呢?
这里有两个理解方式。
第一个是用传统通信的方式理解。
从一个有噪声的信号\(r(t)\)中找出需要的预期信号\(s(t)\),需要对收到的信号\(r(t)\)和\(s(t)\)做互相关。
互相关是什么?
互相关的定义.
信号\(f(x)\)和\(h(x)\)的互相关:
\(R_{fh}=\int_{- \infty}^{+ \infty}f^*(\tau-x)h(\tau)d\tau\)
互相关不满足交换定理,有:
\(R_{fh}(x)=R^*_{hf}(-x)\)
是不是觉得这个式子看起来很熟悉?没错,长得很像卷积
我们来看看卷积的定义式:
\(f(x)*h(x)=\int_{- \infty}^{+ \infty}f(x-\tau)h(\tau)d\tau\)
我们再把上面的互相关定义是考察一下:
\(R_{fh}=\int_{- \infty}^{+ \infty}f^*(\tau-x)h(\tau)d\tau=\int_{- \infty}^{+ \infty}f^*[-(x-\tau)]h(\tau)d\tau=f^*(-x)*h(x)\)
看出来了嘛?互相关就是对需要的信号的负共轭求一个卷积
所以脉冲压缩就是对接收信号\(r(t)\)和预期信号(发射信号)\(s^*(-t)\)进行卷积。
第二个是从雷达的方式理解。
我们雷达发射的信号是一个LFM信号,作为一个调角信号,且是调频信号,相位有载波频率和时间的二次项。
脉冲压缩结果,为了让时域能量集中,要得到sinc函数的形式。而要得到时域上的sinc函数,sinc函数可以用频域上的矩形函数进行傅里叶逆变换。
为了取得好的脉冲压缩,必须对接收信号进行处理,使得频谱幅度非常平坦(从而可以得到频域上近似矩形函数,来ift到时域上的sinc函数),所以我们需要相位仅包含常量和线性分量。
如何得到这样的频域平坦频谱?
我们知道,雷达发射的LFM信号:
\(s(t)=rect(\frac{t}{T})exp(j\pi Kt^2)\)
是有二次相位的(\(t^2\))
为了得到方波形状的平坦频谱,也就是需要将相位变成线性相位。
在频域,可以与含有二次共轭相位的类似频谱信号相乘,相乘后信号相位就是线性的。
【匹配滤波器的实现】
我们接受的信号,可以看作是发射信号带有了\(t_0\)的时延:
\(s_r(t)=rect(\frac{t-t_0}{T}exp({j\pi K(t-t_0)^2}))\)
第一种方式,传统的通信理解方式,就是在时域构造发送信号的复共轭为滤波器:
\(h(t)=rect(\frac{t}{T})exp({-j\pi K(-t)^2})\)
压缩结果:
\(s_{out}(t)=Tsinc(KT(t-t_0))\)
第二种方式,从频域构造平缓的频域结果,从而ift得到时域的sinc函数,来完成压缩的效果:
由驻定相位原理(POSP),回波信号:
\(s_r(t)=rect(\frac{t-t_0}{T}exp({j\pi K(t-t_0)^2}))\)
的频域表示可以写作:
\(S_r(t)=rect(\frac{f}{|K|T})exp({-j\pi \frac{f^2}{K}})exp({-j2\pi ft_0})\)
我们的匹配滤波器应该要消除二次相位,注意频域相乘->时域卷积,
消去二次相位,只要相乘一个\(H(t)=rect(\frac{f}{|K|T})exp({+j\pi \frac{f^2}{K}})\)
输出的频谱信号为:
\(S_{out}=S_r(f)H(f)=rect(\frac{f}{|K|T})exp({-j2\pi ft_0})\)
输出压缩结果:
\(s_{out}=|K|Tsinc{KT(t-t_0)}\)
两个时域上的压缩结果都是sinc函数形式,但是用第二种方式的结果比第一种方式多了一个幅度上的系数|K|。
是因为使用驻定相位原理时忽略了一个\(\frac{1}{\sqrt{|K|}}\)
实际使用会用归一化准则,可以忽略不计。
(以下为四处搜罗的原始参考资料)
【为什么要脉冲压缩?】解决距离分辨率和作用距离之间的矛盾

为了解决传统单频脉冲面临的作用距离和空间分辨率之间的矛盾,脉冲压缩技术采用这样的策略:
发射宽度相对较宽而峰值功率低的脉冲,使信号有足够的能量以保证作用距离;
接收时做匹配滤波,将底峰值的宽脉冲压缩成高峰值的窄脉冲,避免脉冲重叠现象,从而提高空间分辨率。
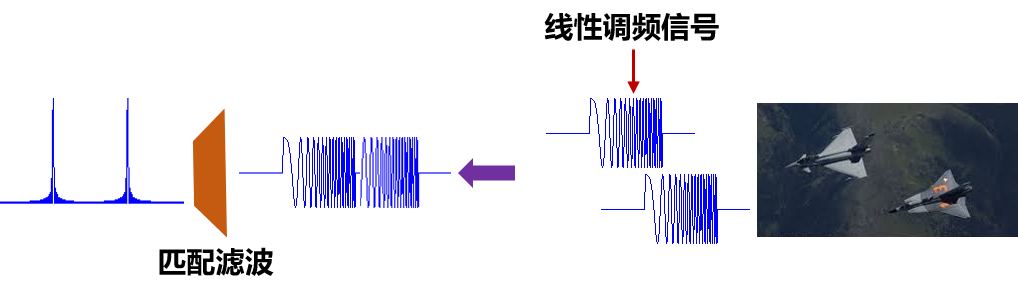
也就是说,发送的是宽带宽、低功率脉冲,低功率是为了后续方便筛选出来。
匹配滤波。
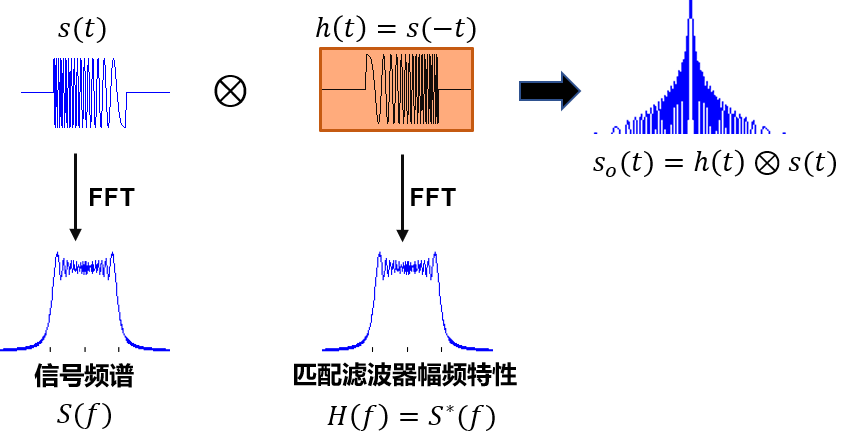
为了实现压缩,在接收机上设置一个与发射信号“共轭匹配”的压缩网络。【相位共轭匹配】
时域上,匹配滤波器的冲击响应函数构造为**输入信号的镜像**;频域上,匹配滤波器的幅频特性与信号的幅频特性一致。
当信号通过匹配滤波器时,信号越强的频率点,滤波器的放大倍数也越大;信号越弱的频率点,滤波器的放大倍数也越小,从而使信号在时域更集中。
另外一方面,从相频特性上看,匹配滤波器的相频特性和输入信号正好完全相反。
这样,通过匹配滤波器后,信号的相位为0,正好能实现信号时域上的相干叠加。
而噪声的相位是随机的,只能实现非相干叠加。这样在时域上保证了输出信噪比的最大。
【匹配滤波器定义】

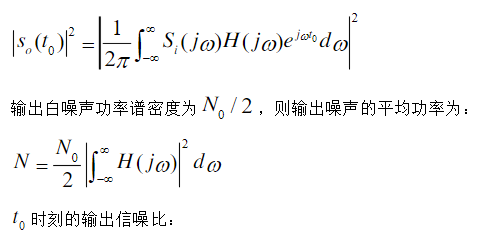

【匹配滤波器性质】


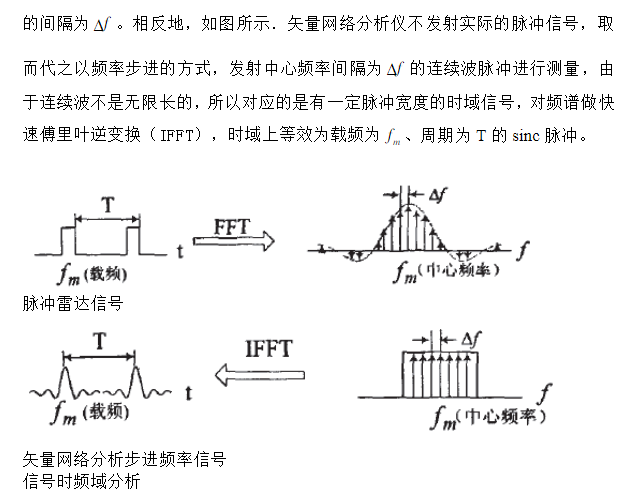
【LFM信号通过匹配滤波器后】

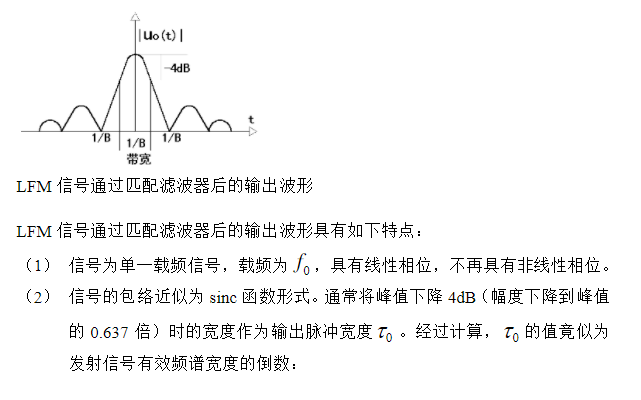

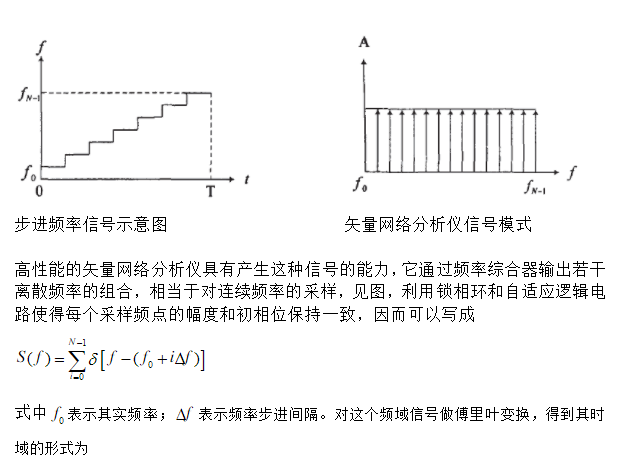

【参考文献】
http://www.pantsiao.com/wiki/脉冲压缩(pulse-compression)/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号