杨辉三角形

给定一个正整数 N，请你输出数在杨辉三角 中第一次出现N 是在第几个数？

思路

参考

杨辉三角特点:

1. 对称性
   杨辉三角形左右两边数字对称相等。

2. 渐增性
   越往中间数字越大，除最外层1外，越往下数字越大。

3. 组合数
   杨辉三角形里面的每一个元素都能用组合数表示。第\(N\)行的第\(M\)列可以表示成\(C(N-1,M-1)\)，如6在第5行的第3列，它对应的组合数就是\(C(5-1,3-1)\)，即\(C(4,2)\)。

解题思路

• 因为要找出第一次N出现的位置，根据对称性可知，N出现的位置必定在左边，因此只考虑左半边位置即可。
• 由于每个斜方向的数都是逐增的，因此考虑在斜方向二分；并且根据组合数性可知，可以通过位置计算出该位置的值，因此可以在每个斜方向二分位置，二分过程是通过将该位置的数和\(N\)比较。

然后问题就是：

1. 如何找到每个斜行？
   for循环遍历是第几层斜行即可。因为在内斜行中元素总是较先出现的，所以我们要从内斜行开始从内往外开始找，

2. 如何确定每个斜行的初始位置和终止位置？
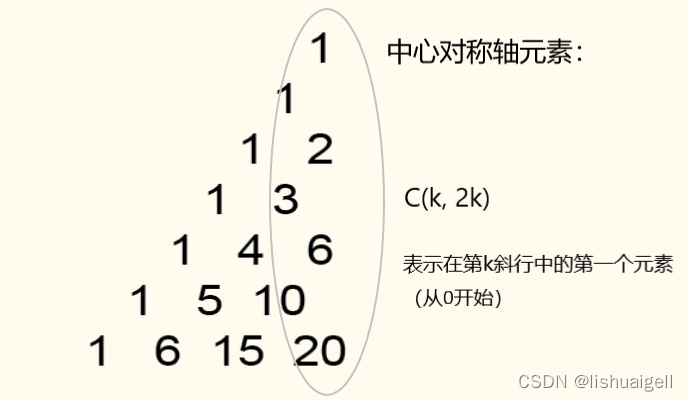
   可以发现中心对称轴的元素是每一斜行中最小的，它的特点是 \(C( k, 2k )\) 。
   以目标值作为终止位置即可。
   

3. 找多少斜行？
   如果该斜行最小元素都已经超出10的9次方那么剩下的元素都是大于10的9次方的，也就是说这一斜行是没有意义的，不用考虑。经计算，只有16斜行以内的数才符合条件。

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long 
int n;
//前大后小
int C(int x,int k){
    int ans=1;
    for(int i=x,j=1;j<=k;i--,j++){
        ans=ans*i/j;
        if(ans>n)return ans;
    }
    return ans;
}

int solve(int x){
    int l=2*x , r=max(n,l);
    while(l<r){
        int mid=l+(r-l)/2;
        int val=C(mid,x);
        if(val>=n) r=mid;
        else  l=mid+1;
    }
    if(C(r,x)!=n) return 0;
        cout<<(r * (r + 1) / 2) + x + 1<<endl;
    return 1;
}
signed main()
{
    cin>>n;
    for(int i=17;i>=0;i--)
        if(solve(i)) break;
    return 0;
}