基2时抽8点FFT的matlab实现流程及FFT的内部机理

前言

本来想用verilog描述FFT算法，虽然是8点的FFT算法，但写出来的资源用量及时延也不比调用FFT IP的好，

还是老实调IP吧，了解内部机理即可，无需重复发明轮子。

 参考

https://wenku.baidu.com/view/6f5862997c1cfad6185fa725.html

https://blog.csdn.net/shengzhadon/article/details/46737517

流程

FFT能做什么在此就不赘述了，只了解数据的运算流程。

1.FFT的基本公式：

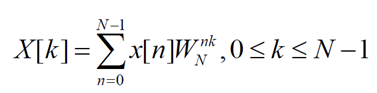
第一眼看这个公式，肯定是脑袋瞬间宕机。

2.旋转因子：记住旋转因子具有可约性，对称性，周期性。

表示方法有两种，通过欧拉公式转换，本质上是一致的。

Wn=exp(-j*2*k*pi/N) ，N表示FFT点数，k表示第几个旋转因子。

Wn = cos(2*pi*k/N) - i*sin(2*pi*k/N)

第二次脑袋瞬间宕机。

3.蝶形图：

好在数学家为了普通人类能理解公式，绘制了帅气的蝴蝶漫画图，8点FFT的如下：

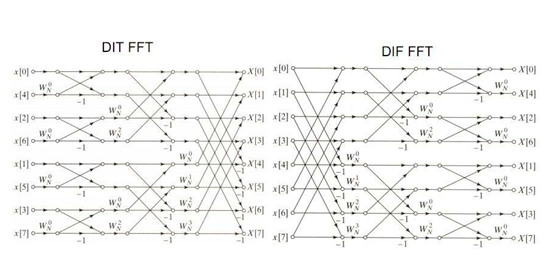
不直观，添加几条辅助线再看：可以看到分为三级蝶形运算。

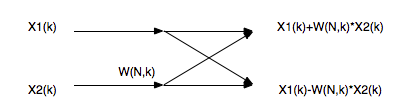
比如第一级的蝶形运算结果：x0’=x[0]+x[4]*w0,x1’=x[0]-x[4]*w0。其他节点以此类推。

注意-1的位置和旋转因子的位置。注意数据和旋转因子都是复数，这就是说蝶形图中的乘法和加减都是复数运算。

而所谓代码实现，不管什么代码，本质上就是对各级的公式进行实现，从而得到结果。

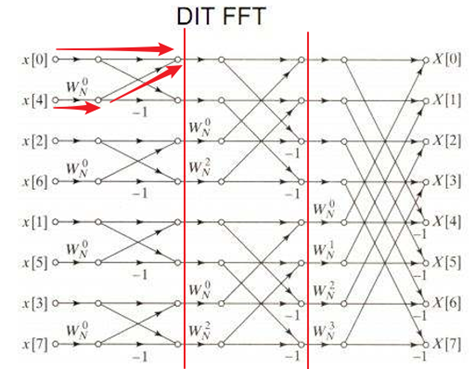
觉得讲得不清楚，那么看下图更直观：当然图中少标识了-1。

4.数据输入倒序：

 从上图左侧可以看到，序列按照了一定的规则进行了倒序，如果按照顺序进行数据输入，肯定是不正确的。十进制可能看不出来，但使其转换为二进制表示就可以知道：

 

5.Matlab验证算法：

到这一步，就可以把蝶形结构用matlab语言描述出来了。蝶形因子进行了2^16次放大，数据经过了两级放大，结果需除去放大因子。

x序列为fs=500hz采样下的125hz且有直流分量的8点采样信号。

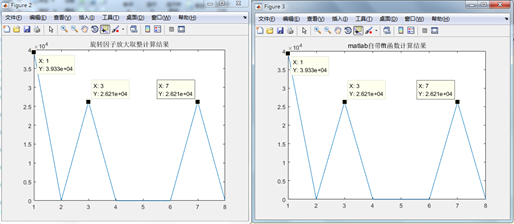
clc;
clear all;
close all;
%放大了2^16次的系数
w0 = 65536;
w1 = 46341 - 46341*i;
w2 = -65536*i;
w3 = -65536 - 65536*i;
% w0 = 1;
% w1 = 0.7071 - 0.7071*1i;
% w2 = -1i;
% w3 = -0.7071 - 0.7071*1i;
x = [4916,11469,4916,-1638,4916,11469,4916,-1638];
%%第一级蝶形运算,没有放大
x1(1)=x(1)+x(5);  
x1(2)=x(1)-x(5);  
x1(3)=x(3)+x(7);  
x1(4)=x(3)-x(7);  
x1(5)=x(2)+x(6);  
x1(6)=x(2)-x(6); 
x1(7)=x(4)+x(8);  
x1(8)=x(4)-x(8);  
%%第二级蝶形运算放大了65536，因为系数放大了2^16，其他部分应当相应的放大
x2(1)=x1(1)*65536+x1(3)*65536;  
x2(2)=x1(2)*65536+x1(4)*(w2);  
x2(3)=x1(1)*65536-x1(3)*65536;  
x2(4)=x1(2)*65536-x1(4)*(w2); 
x2(5)=x1(5)*65536+x1(7)*65536;  
x2(6)=x1(6)*65536+x1(8)*(w2); 
x2(7)=x1(5)*65536-x1(7)*65536; 
x2(8)=x1(6)*65536-x1(8)*(w2);  
%%第三级蝶形运算放大了65536，因为系数放大了2^16，其他部分相应的进行放大
y(1)=x2(1)*65536+x2(5)*65536;
y(2)=x2(2)*65536+x2(6)*(w1);  
y(3)=x2(3)*65536+x2(7)*(w2); 
y(4)=x2(4)*65536+x2(8)*(w3);  
y(5)=x2(1)*65536-x2(5)*65536;  
y(6)=x2(2)*65536-x2(6)*(w1); 
y(7)=x2(3)*65536-x2(7)*(w2); 
y(8)=x2(4)*65536-x2(8)*(w3);  
% plot(abs(y/(65536^3))-abs(fft(x)))
figure;
plot(x);
title('x value');
figure;
plot(abs(y/(65536^2)));
title('旋转因子放大取整计算结果');
figure;
plot(abs(fft(x)));
title('matlab自带fft函数计算结果');

6.查看一下劳动成果：可以看到matlab自带的FFT和手动蝶形算出的FFT结果是一致的。

7.转成verilog描述，无非就是对各级的蝶形公式进行相关的实现。

注意：（1）乘法和加减法为复数运算。

（2）各级位宽需要注意，避免溢出。

看到蝶形图及相关公式，可以看到还是有点算法复杂度的。

虽然可以手敲实现，但FPGA厂商已经提供了足够好用的FFT IP core，资源量和计算延迟都很nice，

所以还是老实用IP吧。哈哈

8.FFT的一些性质：

（1）采样速率和点数的关系：

频谱分辨率△f=fs/N。点数和采样速率共同决定了FFT的频谱分辨率。

某一个点的频率关系：f=k*fs/N。注意FFT计算结果的第一点为直流分量。

（2）栅栏效应及补零处理：

频谱分辨率决定了透过栅栏窗子看真实频谱的真实度。补零可使得离散谱外观更加平滑，同时增长序列长度。

（3）FFT变换后的频域模幅度对应关系：

FFT计算出的第0个点为直流分量，其模值为直流分量的N倍。其余位置求得的模值需要除以N/2，才为真实的模值。

第0点：模值/N

其他频率点:模值/(N/2)

（4）频域幅度及相位计算：

某点（im,re）的幅度信息为：sqrt（im^2+re^2），即实部平方加虚部平方开根号。

相位为：atan（im/re），反三角算即可，即为本频谱时域的初相。

 

以上。