平衡二叉树、红黑树、B树、B+树总结
平衡二叉树(AVL树)
平衡二叉树具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
作用:当原序列有序时,提高搜索效率。
平衡因子:平衡二叉树中不存在平衡因子大于 1 的节点。在一棵平衡二叉树中,节点的平衡因子只能取 0 、1 或者 -1。
最小失衡子树:在新插入的结点向上查找,以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。失衡调整主要是通过旋转最小失衡子树来实现的。
四种插入方式旋转情况
1、A的左孩子的左子树插入节点(LL)

2、A的右孩子的右子树插入节点(RR)

3、A的左孩子的右子树插入节点(LR)
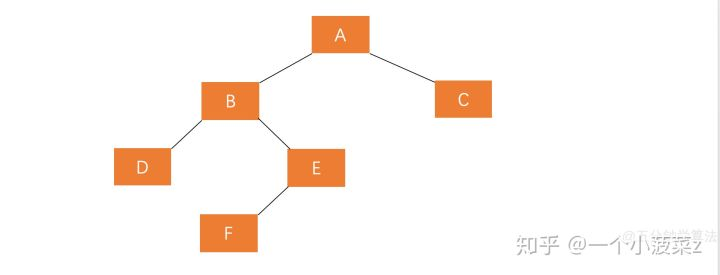

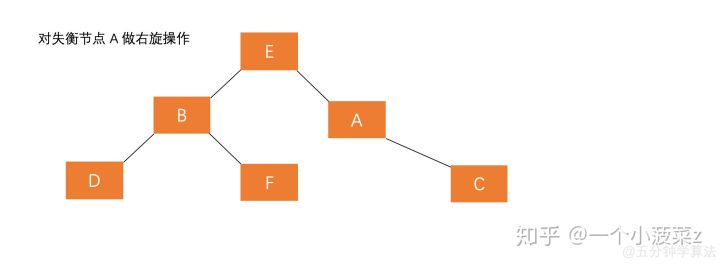
4、A的右孩子的左子树插入节点(RL)
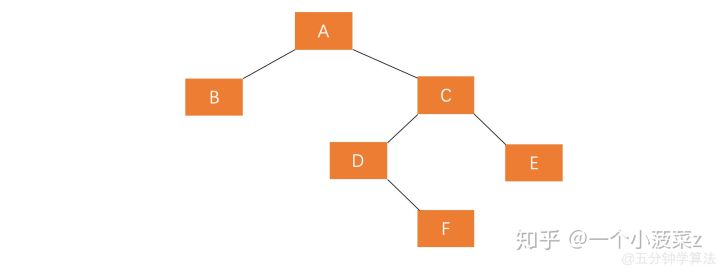
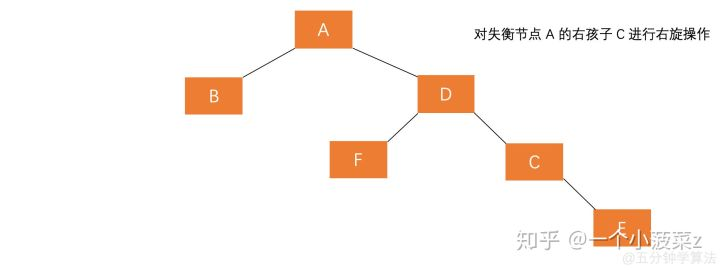

删除操作
插入操作后只需要对插入栈中的弹出的第一个非平衡节点进行修正,而删除操作需要修正栈中的所有非平衡节点。
四种情况:
删除叶子节点、删除的节点只有左子树、删除的节点只有右子树、删除的节点既有左子树又有右子树
B树
B树的创建就是为了优化数据库查找。
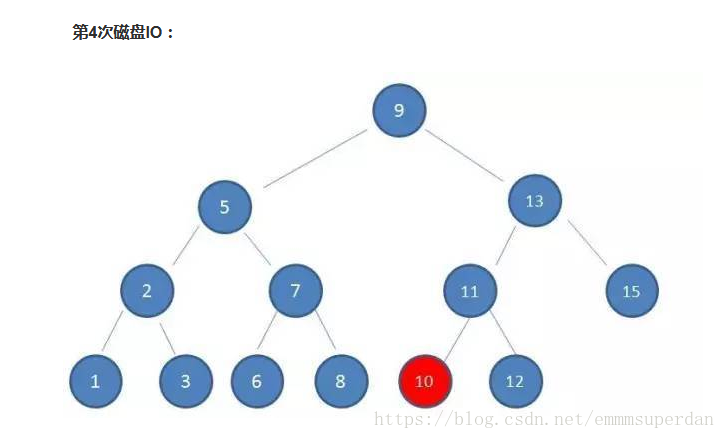
调整成B树结构如下:

一颗m阶的B树定义如下:
1、每个结点最多有m-1个关键字。
2、根结点最少可以只有1个关键字。
3、非根结点至少有Math.ceil(m/2)-1个关键字。
4、每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
5、所有叶子结点都位于同一层,或者说根结点到每个叶子结点的长度都相同。
B+树
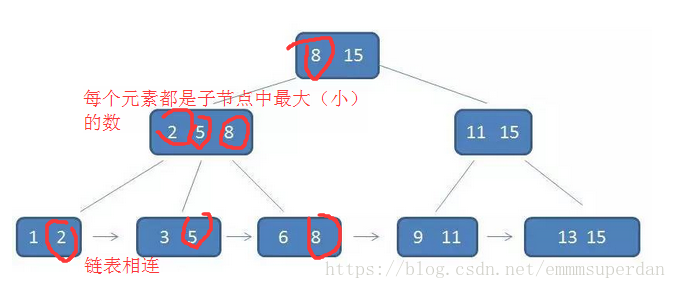
1、单一节点存储更多的元素,使得查询的IO次数更少。(非子叶结点都存放的是索引,只有叶子结点才带有卫星数据;而B树的每个节点都有卫星数据,那这样B+树的结点会多出空间来放元素,也意味着B+树比B树还要矮胖);
2、所有查询都要查找到叶子节点,查询性能稳定。(B树最好的情况是根结点就是结果,最坏是叶子结点;而B+树的数据都要在叶子结点中的卫星数据获取)
3、所有叶子节点形成有序链表,便于范围查询。(如果想查询一个范围,B树的时间复杂度要比B+树高很多)
红黑树
红黑树是一种自平衡二叉查找树,主要是为了解决二叉查找树多次插入新节点而导致的不平衡提出。
红黑树的查找、删除、添加操作都为log(n)。
红黑树近似平衡:深度最大的节点的深度<= 2 * 深度最小的节点的深度。
应用:Linux进程调度、HashMap、TreeMap、C++中的map和set、epoll在内核中的实现(用红黑树管理事件块)、nginx(用红黑树管理timer)。
性质:



