软工第三次作业——个人项目作业

项目 | 内容
-|-|-
这个作业属于哪个课程 |2020春季计算机学院软件工程（罗杰、任建）
这个作业的要求在哪里 |个人项目作业
我在这个课程的目标是 | 提高软件开发能力、团队协作能力
这个作业在哪个具体方面帮助我实现目标 | 个人开发实践
教学班级|006
项目地址|https://github.com/kongkongNG/Intersection_proj


一、PSP表格

PSP2.1 Personal Software Process Stages 预估耗时（分钟） 实际耗时（分钟）
Planning 计划
· Estimate 估计这个任务需要多少时间 30 30
Development 开发
· Analysis 需求分析 (包括学习新技术) 30 40
· Design Spec 生成设计文档 60 20
· Design Review 设计复审 (和同事审核设计文档) 20 5
· Coding Standard 代码规范 (为目前的开发制定合适的规范) 10 5
· Design 具体设计 60 60
· Coding 具体编码 120 240
· Code Review 代码复审 30 60
· Test 测试（自我测试，修改代码，提交修改） 60 360
Reporting 报告
· Test Report 测试报告 40 20
· Size Measurement 计算工作量 20 10
· Postmortem & Process Improvement Plan 事后总结, 并提出过程改进计划 60 30
合计 540 880

　　从表格中可以看到，事前预估的编码与测试的时间估计差距比较大，原因总结如下：

  1. 设计时本着“先让它跑起来”的想法，对于一些精度、边界问题没有考虑充分，导致测试时bug层出不穷。
  2. 编码时对于C++的容器、某些特性不够熟悉，边查边写导致效率很低。这里充分体会到了讲义里技能的反面所说的痛处。
  3. 在家里惰性较重，常常分心导致思路不连贯。

二、解题思路描述

　　刚拿到题目，首先思考的是寻找通过数学技巧直接判断交点数而无需求交点的方法，然而当考虑到可能会出现重复交点的情况，数学技巧只能求最少交点数与最大交点数，进而转向暴力求解交点，并通过比较去重的方法。

　　之后开始通过计算验证和查找的方式得到各种交点公式，判断可行性。所有用到的公式都放在设计文档的“数学准备”一栏中，故不再赘述。

　　接下来考虑的是交点去重问题。查资料得知C++的set类采用RB树的数据结构，能够自动去重，所以选择set作为储存交点的数据结构。


三、设计实现过程。

　　本次项目的实现思路为：每次接收一个几何对象时，判断它与之前存下的所有几何对象是否相交，若相交则求交点，并加入交点的set集合。

　　类的设计大致是：通过一个Geometry类作为几何对象的总纲，其中有判断是否相交和求交点两个函数，Line类和Circle类实现这个接口；Intersection类负责实现接受外部参数、实现业务的功能。

　　如图为Line类, Circle类与Geomtry类的关系：

md_2020-03-09-23-13-20.png

　　由于关键函数中的内容基本为数学公式的编码，故下面只展示基本需求——求两直线交点的流程图：
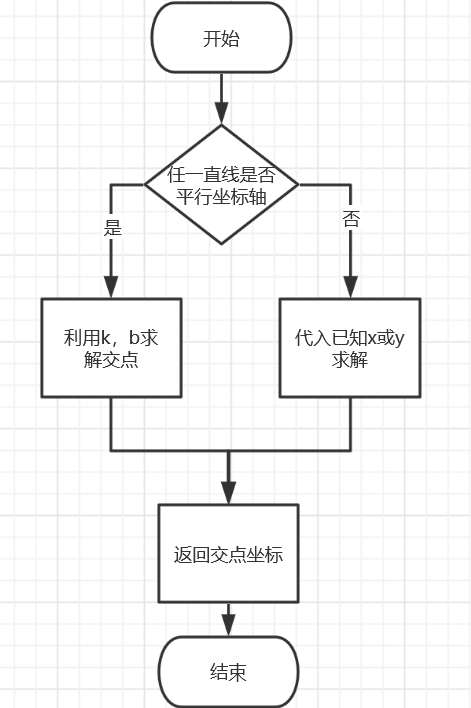
md_2020-03-09-23-28-26.png

　　单元测试的设计有常规样例测试与边界样例测试，检测几何对象之间是否相交以及相交得到的交点坐标是否准确。其中，直线与直线的相交检测考虑：任一条直线与坐标轴平行、两条直线都与坐标轴平行、两条直线都不与坐标轴平行三种情况；直线与圆相交检测考虑：直线与圆相交、直线与圆相切、直线与圆相离、直线与坐标轴平行四种样例；两圆相交检测：两圆相交、两圆内切、两圆外切、两圆内离、两圆外离五种情况；多个几何对象测试中考虑交点重合以及不重合的情况。


四、性能分析

　　这里的性能分析采用的输入数据是1000+组直线数据：
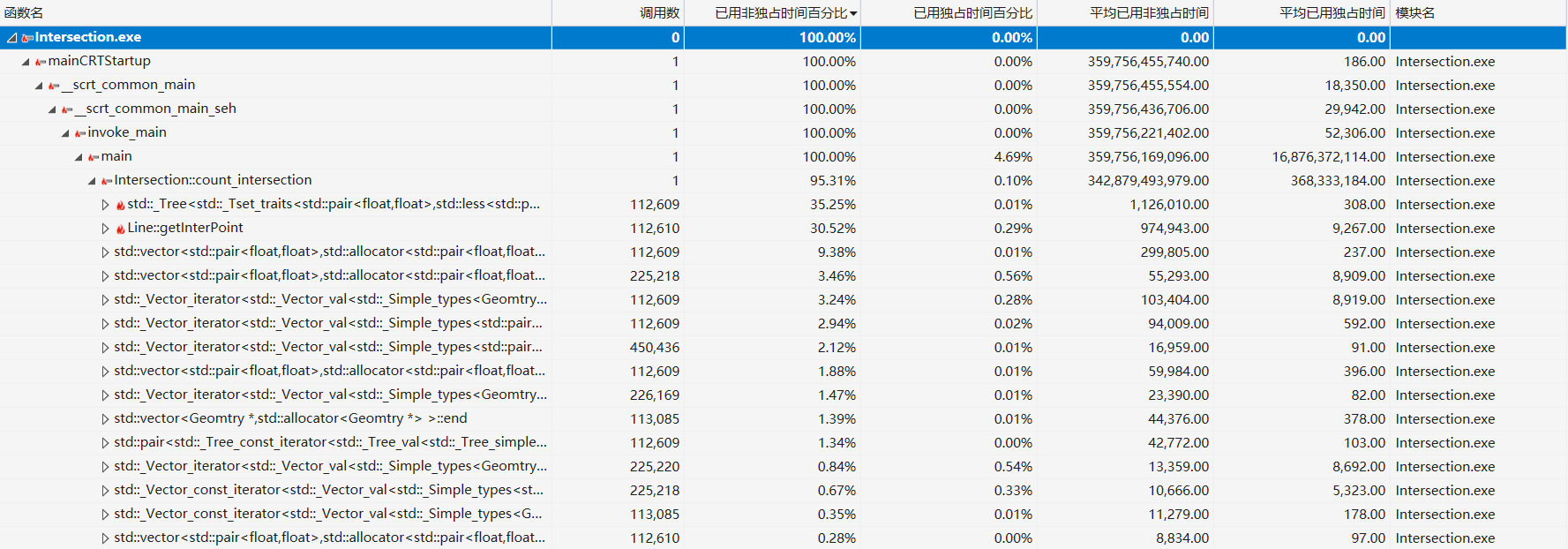
md_2020-03-10-10-21-34.png

　　从图中可以看到，在main中开销最大的是主业务函数count_intersection()，其中，有两个“热函数”：std::_Tree的构造函数（也就是set的插入与去重），以及Line::getInterPoint()（即直线的交点计算函数）

　　性能改进大概花费了1h左右，改进的地方不多，思路是将中间运算尽可能简化，比如将相同的开方操作、乘除运算等重复运算提前算出结果，重复使用。


五、代码说明。

1）直线与直线相交

相交检测：

if (this->isVerticalToX()) {
    if (ln->isVerticalToX()) {
        return false;
    }
    else {
        return true;
    }
}
if (ln->isVerticalToX()) {
    if (this->isVerticalToX()) {
        return false;
    }
    else {
        return true;
    }
}
		return fabs(this->k - ln->k) > EPS;

　　思路很简单，就是考虑垂直坐标轴的直线后，判断k是否相等（这里用fabs()>EPS考虑了double的精度问题），从而判断两直线是否平行，平行则无交点。

求交点：

if (this->isVerticalToX()) {
    x = this->x;
    y = ln->k * x + ln->b;
}

else if (ln->isVerticalToX()) {
    x = ln->x;
    y = this->k * x + this->b;
}

else {	// no need to consider vertical to y because we can handle it
    x = (ln->b - this->b) / (this->k - ln->k);
    y = this->k * x + this->b;
}

pvec.push_back({ x, y });

　　由于采用斜率式的储存方法，所以当直线垂直于X轴时，交点的x值可以直接取得（在输入中作了判断并存值）。代码中注释的意思是：当某直线垂直于Y轴时，无需特殊考虑，因为仍可以通过公式正常求解（不会出现两条直线都垂直Y轴的情况，已经通过相交检测过滤）。其他正常直线通过公式求解即可得到交点。

2）直线与圆相交

相交检测：

if (isVerticalToX()) {
    d = fabs(cc->n - this->x);
}
else if (isVerticalToY()) {
    d = fabs(cc->m - this->b);
}
else {
    up = this->k * cc->n - cc->m + this->b;
    down = sqrt(this->k * this->k + 1);
    d = fabs(up / down);
}

if (d > cc->r) {
    return false;
}
else {
    return true;
}

　　思路是：考虑直线垂直于X轴、垂直于Y轴与正常直线三种情况时圆心到直线距离，通过距离与圆半径的比较即可得到圆与直线相交关系：d<r则相交，否则不相交（这里将相切与相交合并为相交，因为求交点时会通过求得的值判定交点是1个还是2个）

求交点：

A = 1 + k * k;
B = 2 * k * (b - cc->m) - 2 * cc->n;
C = (b - cc->m) * (b - cc->m) + cc->n * cc->n - cc->r * cc->r;
vector<double> ans = Geomtry::solve(A, B, C);
for (auto it = ans.begin(); it != ans.end(); it++) {
    double yi = k * *it + b;
    pvec.push_back({ *it, yi });
}

　　垂直坐标轴的特殊直线与圆交点求法就是带入已知x值或y值，利用几何知识求解，代码不再赘述。上述代码是正常直线与圆相交的情况，数学公式见设计文档的“数学准备”一栏，思路是得到直线与圆相交的一元二次方程组后，通过Geomtry::solve(A, B, C)求解方程得到横坐标（如果相切只返回一个），然后带入直线得到纵坐标。

3）两圆相交

相交检测：

double dcenter = sqrt((n - cc->n) * (n - cc->n) 
	+ (m - cc->m) * (m - cc->m));	// d = sqrt((x1-x2)^2 + (y1-y2)^2)
if (dcenter > r + cc->r || dcenter < fabs(r - cc->r) ) {
	return false;
}
else {
	return true;
}

　　思路是通过计算两圆心距离与半径关系进行判断。若圆心距大于半径之和，表示两圆外离；若圆心距小于半径差的绝对值，表示两圆內离。其他情况为存在交点。

求交点：

d = sqrt((n - cc->n) * (n - cc->n)
        + (m - cc->m) * (m - cc->m));	// distance of two centers
AE = (this->r * this->r - cc->r * cc->r + d * d) / (2 * d);
x0 = this->n + AE / d * (cc->n - this->n); // x0 = x1 + AE/d * (x2-x1)
y0 = this->m + AE / d * (cc->m - this->m); // x0 = x1 + AE/d * (x2-x1)
CE = sqrt(r * r - AE * AE); // CE^2 + AE^2 = AC^2 = r^2

x1 = x0 - CE / d * (cc->m - m);
y1 = y0 + CE / d * (cc->n - n);
x2 = x0 + CE / d * (cc->m - m);
y2 = y0 - CE / d * (cc->n - n);

if (x1 == x2 && y1 == y2) {
    pvec.push_back({ x1, y1 });
}
else {
    pvec.push_back({ x1, y1 });
    pvec.push_back({ x2, y2 });
}

　　同样是几何关系推演得到的结果进行编码，公式在设计文档的“数学准备”一栏能找到。推导思路是先求得两圆交点连线与圆心连线的交点，再通过相似三角形的性质得到横纵坐标。

4）主逻辑

for (auto it = geoms.begin(); it != geoms.end(); it++) {
    if (gmt->isInterset(*it)) {
        vector<Point> pvec = gmt->getInterPoint(*it);
        for (auto pIt = pvec.begin(); pIt != pvec.end(); pIt++) {
            pIt->id = points.size();
            points.insert(*pIt);
        }
    }
}
geoms.push_back(gmt);

　　主程序的思路就是每次将输入的几何对象与当前所有几何对象做相交检测，若存在交点，则计算交点并加入点集。其中gmt是当前输入的几何对象，geoms是几何对象集合，points是结构体Point的set集合，能够通过operator<的判断进行去重。Point中重写了operator<，在精度范围内两个点相同则返回false。

　　下面是Point结构体的细节：

struct Point {
	double x, y;
	Point(double x, double y) : x(x), y(y) {}

	bool operator<(const Point &p) const
	{
		if (fabs(x - p.x) <= EPS && fabs(y - p.y) <= EPS) {
			return false;
		}
		else {
			return (x!=p.x)? x < p.x : y < p.y;
		}	
	}
};

六、代码分析与单元测试结果

代码分析

消除警告前：

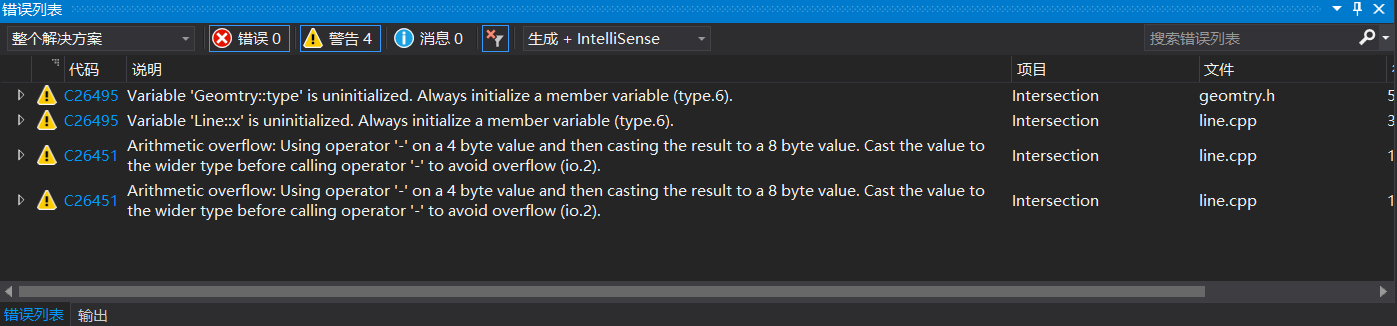
md_2020-03-10-16-37-34.png

代码中存在的问题及解决办法如下：

  • C26435：存在未初始化的成员。解决办法是给每个可能无初值的成员赋初值
  • C26451：算术溢出，将4byte的值用于减法运算并赋给8byte的结果。解决办法是在int型数据前强制转换为double参与减法运算。

消除警告后：

md_2020-03-10-16-41-43.png

单元测试结果

　　单元测试的测试文件按照“三、设计实现过程”中的设计来完成，即直线与直线、直线与圆、圆与圆以及总体业务逻辑测试，测试结果如下：

md_2020-03-10-18-41-02.png

posted @ 2020-03-10 17:23  kingkongk  阅读(226)  评论(2)  编辑  收藏  举报