1894: 985的方格难题

Time Limit: 1 Sec  Memory Limit: 128 MB
Submit: 325  Solved: 59

SubmitStatusWeb Board

Description

985走入了一个n * n的方格地图，他已经知道其中有一个格子是坏的。现在他要从(1, 1)走到(n, n)，每次只可以向下或者向右走一步，问他能否到达（n，n）。若不能到达输出-1，反之输出到达（n，n）的方案数。

Input

第一行输入一个整数t，代表有t组测试数据。

每组数据第一行输入三个整数n，x，y，分别代表方格地图的大小以及坏掉格子的位置。

注：1 <= t <= 20，1 <= n <= 30，1 <= x，y <= n。

Output

若可以到达（n，n）则输出方案数对1e9 + 7取余的结果，反之输出-1。

Sample Input

22 1 22 2 2

Sample Output

1-1

HINT

Source

hpu

解题思路：从（1,1）到达（n，n）有两种情况，1：不经过（x，y）；2：经过（x，y）。所以要求从（1,1）出发不经过（x，y）到达（n，n）的方法数，用从（1,1）到达（n，n）的方法数减去从（1,1）出发经过（x，y）到达（n，n的方法数即可）。

从（1,1）无障碍到达（n，n）的方法数，可有规律：

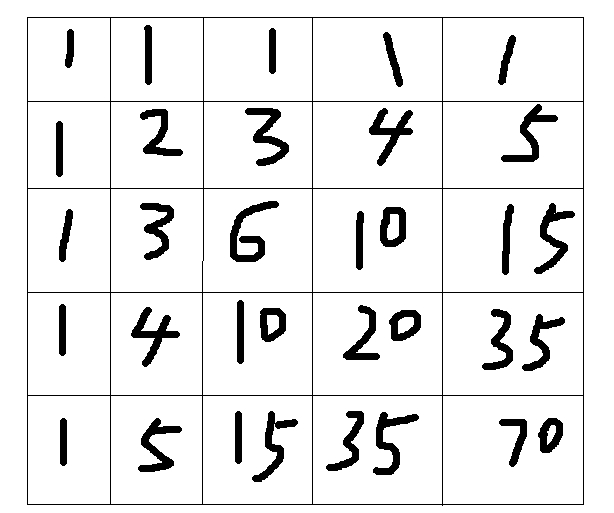
如n等于5，

每个格子里面的数字是从（1,1）到达该格子的方法数，可发现，除了第一列和第一行，每个数都等于它上面的数和左边的数之和，于是打表能得到从（1,1）到达每个点的方法数。设陷阱的坐标为（x，y），那么从（1,1）到（x，y）的方法数s1可在图中找出，而（x，y）到（n，n）的方法数s2可以将（x，y）当做（1,1），（n，n）转化成相对坐标，那么从（x，y）到（n，n）的方法数也求了出来，s1*s2即为从（1,1）经过（x，y）到（n，n）的方法总数，然后用map【n】【n】-s1*s2即可。

代码如下：

#include <cstdio>  
#define MOD 1000000007  
long long n,x,y;  
long long map[31][31];  
int main()  
{  
    for(int i=1;i<31;i++)  
    {  
        map[1][i]=1;  
    }  
    for(int i=1;i<31;i++)  
    {  
        map[i][1]=1;  
    }  
    for(int i=2;i<31;i++)  
    {  
        for(int j=2;j<31;j++)  
        {  
            map[i][j]=map[i-1][j]+map[i][j-1];  
        }  
    }  
    int t;  
    scanf("%d",&t);  
    while(t--)  
    {  
        scanf("%lld%lld%lld",&n,&x,&y);  
        if(n==x&&x==y)//点（n，n）是格盒子，那么就走不到  
        {  
            printf("-1\n");  
            continue;  
        }  
        if(x==1&&y==1)//出发点为坏格子，那么也无法走  
        {  
            printf("-1\n");  
            continue;  
        }  
        long long ans=map[n][n]-map[x][y]*map[n-x+1][n-y+1];//第一个map是方法总数，第二个map是从出发点到（x，y）的方法数，第三个map是从（x，y）到（n，n）的方法数。  
        printf("%lld\n",ans%MOD);//注意取模  
    }  
    return 0;  
}