计算任意多边形的面积及判断顶点的顺或逆时顺序

对于凸多边形，如下图，以多边形的某一点为顶点，将其划分成多个三角形，计算这些三角形的面积，然后加起来即可。已知三角形顶点坐标，三角形面积可以利用向量的叉乘来计算。

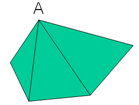
图1

对于凹多边形，如下图，如果以$A$为顶点，将其划分成多个三角形，则多边形的面积 $S= S_{ABC} + S_{ACD} + S_{ADE}$, 这个面积明显超过多边形的面积。

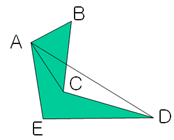
图2

根据二维向量叉乘求三角形ABC面积时，利用的是

\begin{aligned}
& |\overrightarrow{A B} \times \overrightarrow{A C}|=|\overrightarrow{A B}| |\overrightarrow{A C}| \sin (A) \
& S_{A B C}=\frac{1}{2}|\overrightarrow{A B}| |\overrightarrow{A C}| \sin (A)=\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|
\end{aligned}

根据以上公式可知，使用叉乘求面积是有正负的。图2中如果\(S_{ABC}\)和\(S_{ADE}\)是正的，那么\(S_{ACD}\)则是负的，这样加起来刚好就是多边形的面积。对于凸多边形，所有三角形的面积都是同正或者同负。

图3

如果我们不以多边形的某一点为顶点来划分三角形而是以任意一点，如图3，这个方法也是成立的：$S = S_{OAB} + S_{OBC} + S_{OCD} + S_{ODE} + S_{OEA}$

判断顶点的顺或逆时顺序

如图3，只需在任意多边形的所有顶点中找到最右边的顶点\(D\)，即\(x\)最大的顶点，再取\(D-1\)、\(D+1\)点，即\(C\)、\(E\)，再求向量\(\overrightarrow{DC}\)与\(\overrightarrow{DE}\)的向量积，即可判断出顺时针或逆时针，顺序符合“右手定则”.

示例代码：

private bool IsClockWise(Vector2[] points) {
    // 通过计算叉乘来确定方向
    float sum = 0f;
    double count = points.Length;
    Vector3 va, vb;
    for (int i = 0; i < points.Length; i++) {
        va = points[i];
        vb = (i == count - 1) ? points[0] : points[i + 1];
        sum += va.x * vb.y - va.y * vb.x;
    }
    return sum < 0;
}