矩阵运算（平移、缩放、旋转）

(x',y',z')表示新的位置，
(x,y,z)表示当前位置，
(dx,dy,dz)平移的量。

加法2D平移

\[\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ \end{bmatrix} + \begin{bmatrix} dx \\ dy \\ \end{bmatrix} \]

加法3D平移

\[\begin{bmatrix} x' \\ y' \\ z' \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} + \begin{bmatrix} dx \\ dy \\ dz \\ \end{bmatrix} \]

乘法2D平移

\[\begin{bmatrix} x' \\ y' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 1(x) + 0(y) + dx(1) \\ 0(x) + 1(y) + dy(1) \\ 0(x) + 0(y) + 1(1) \\ \end{bmatrix} \]

乘法3D平移

\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & dx \\ 0 & 1 & 0 & dy \\ 0 & 0 & 1 & dz \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 1(x) + 0(y) +0(z) + dx(1) \\ 0(x) + 1(y) +0(z) + dy(1) \\ 0(x) + 0(y) +1(z) + dz(1) \\ 0(x) + 0(y) +0(z) + 1(1) \\ \end{bmatrix} \]

(x',y',z')表示一个点经过缩放后的新位置，
(x,y,z)表示未缩放前的原始位置，
Sx、Sy、Sz分别表示在x轴、y轴和z轴方向上的缩放因子。
注意：计算多个点的缩放，需要将每个点位置分别代入公式计算。

2D缩放

\[\begin{bmatrix} x' \\ y' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} Sx & 0 & 0 \\ 0 & Sy & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} Sx(x) + 0(y) + 0(1) \\ 0(x) + Sy(y) + 0(1) \\ 0(x) + 0(y) + 1(1) \\ \end{bmatrix} \]

3D缩放

\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} Sx & 0 & 0 & 0 \\ 0 & Sy & 0 & 0 \\ 0 & 0 & Sz & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} Sx(x) + 0(y) +0(z) + 0(1) \\ 0(x) + Sy(y) +0(z) + 0(1) \\ 0(x) + 0(y) +Sz(z) + 0(1) \\ 0(x) + 0(y) +0(z) + 1(1) \\ \end{bmatrix} \]

2D旋转

(x',y',z')表示一个点经过旋转后的新位置，
(x,y,z)表示未旋转前的原始位置，
\(\theta\)为旋转角度(编程中以弧度为单位)
注意：计算多个点的旋转，需要将每个点位置分别代入公式计算。

\[\begin{bmatrix} x' \\ y' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} cos \theta & -sin \theta & 0 \\ sin \theta & cos \theta & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} \]

绕Z轴3D旋转

\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} cos \theta & -sin \theta & 0 & 0 \\ sin \theta & cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} \]

绕X轴3D旋转

\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos \theta & -sin \theta & 0 \\ 0 & sin \theta & cos \theta & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} \]

绕Y轴3D旋转

\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} cos \theta & 0 & sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -sin \theta & 0 & cos \theta & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} \]

转换	方法	说明
平移（置换）	translate(tx, ty)	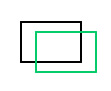将图像 tx 像素向右移动，将 ty 像素向下移动。
缩放	scale(sx, sy)	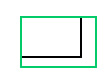将每个像素的位置乘以 x 轴的 sx 和 y 轴的 sy，从而调整图像的大小。
旋转	rotate(q)	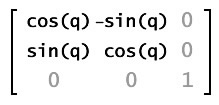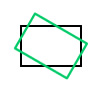将图像旋转一个以弧度为单位的角度 q。
倾斜或剪切	无；必须设置属性 b 和 c	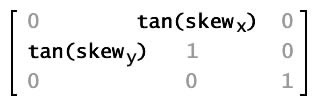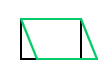以平行于 x 轴或 y 轴的方向逐渐滑动图像。Matrix 对象的 b 属性表示斜角沿 y 轴的正切；Matrix 对象的 c 属性表示斜角沿 x 轴的正切。