三角函数

https://baike.baidu.com/item/三角函数公式/4374733
https://zhuanlan.zhihu.com/p/390928056

\(\frac{sin \alpha}{cos \alpha}=tan \alpha\)
\(\frac{1}{cos^2 \alpha}=1+tan^2 \alpha\)

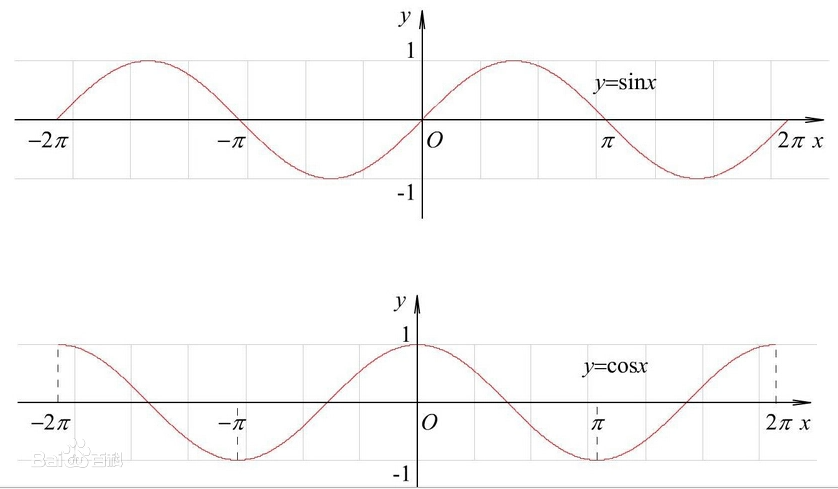
sin与cos函数图像：

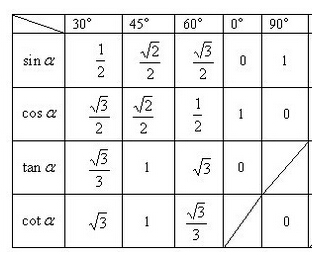
• 证明 $sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2} $

解：
求\(sin(\frac{\pi}{3})\)，相当于求60度角的正弦

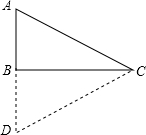
如上图，很容易证明 \(\bigtriangleup ACD\) 各个角都为60度。
∴ \(\bigtriangleup ACD\) 是等腰三角形。
∴ AD=AC=DC。
∵ AB=BD，∴ AB=\(\frac{1}{2}\)AC (在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。)。

设AC=1，则AB=\(\frac{1}{2}\)，BC=$\sqrt{1^2-(\frac{1}{2} )^2 } =\sqrt{1-\frac{1}{4} } =\sqrt{\frac{3}{4} } =\frac{\sqrt{3} }{2} $

∴ \(sin(\frac{\pi}{3})=\frac{BC}{AC}=\frac{\sqrt{3}}{2}\)