Markdown 数学公式输入

好用的 LaTeX 公式编辑器
Mathpix
SimpleTex

圆圈数字序号：
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
⑪ ⑫ ⑬ ⑭ ⑮ ⑯ ⑰ ⑱ ⑲ ⑳

\( S(x)=\frac{1}{1+e^{-x}} \tag{1} \)

$
S(x)=\frac{1}{1+e^{-x}}
\tag{1}
$

\( \begin{equation} \left\{\begin{aligned} f(x)&=\tfrac{1}{12} \cdot r, & g(x) &= \tfrac{1}{24} \cdot x, & x&<12 \\ f(x)&=1, &g(x) &= \tfrac{1}{8} \cdot x - 1, & 12 &\le x < 16 \\ f(x)&=1, &g(x) &= 1, & x &\ge 16 \end{aligned} \right. \end{equation} \)

//其中aligned就是用来公式对齐的，在中间公式中，\ 表示换行， & 表示对齐。在公式中等号之前加&，等号介绍要换行的地方加\就可以了。
$
\begin{equation}
\left\{\begin{aligned}
f(x)&=\tfrac{1}{12} \cdot r, & g(x) &= \tfrac{1}{24} \cdot x, & x&<12 \\
f(x)&=1, &g(x) &= \tfrac{1}{8} \cdot x - 1, & 12 &\le x < 16 \\
f(x)&=1, &g(x) &= 1, & x &\ge 16
\end{aligned}
\right.
\end{equation}
$

\(a+b\)

\[a+b \]

$a+b$    //左边显示
$$a+b$$  //居中显示

\(\vec A\)

$\vec A$

\(x^{y^z} = (1+e^x)^{-2xy^w}\)

$x^{y^z} = (1+e^x)^{-2xy^w}$

\(f(x, y) = x^2 + y^2, x \epsilon [0, 100], y \epsilon \{3, 4, 5\}\)

$f(x, y) = x^2 + y^2, x \epsilon [0, 100], y \epsilon \{3, 4, 5\}$

\((\frac {x} {y})^2 , \left(\frac {x} {y} \right)^2\)

$(\frac {x} {y})^2 , \left(\frac {x} {y} \right)^2$

\(\tbinom{n}{m}\)

$\tbinom{n}{m}$

\(\left. \frac{du}{dx} \right| _{x=0}\)

$\left. \frac{du}{dx} \right| _{x=0}$

\(\frac{1}{2x+1} , {{1} \over {2x+1}}\)

$\frac{1}{2x+1} , {{1} \over {2x+1}}$

\(\sqrt[3]{9}, \sqrt{16}\)

$\sqrt[3]{9}, \sqrt{16}$

\(f(x_1,x_2,\ldots,x_n) = x_1^2+x_2^2+\cdots+x_n^2\)

$f(x_1,x_2,\ldots,x_n) = x_1^2+x_2^2+\cdots+x_n^2$

\(\vec a \cdot \vec b = 0\)

$\vec a \cdot \vec b = 0$

\(\int_0^1x^2dx\)

$\int_0^1x^2dx$

\(\lim_{n\rightarrow+\infty}\frac{1}{n(n+1)}\)

$\lim_{n\rightarrow+\infty}\frac{1}{n(n+1)}$

\(\sum_1^n\frac{1}{x^2}, \prod_{i=0}^n{1 \over {x^2}}\)

$\sum_1^n\frac{1}{x^2}, \prod_{i=0}^n{1 \over {x^2}}$

\(\alpha \beta \gamma \Gamma \delta \Delta \epsilon \varepsilon \zeta \eta \theta \Theta \vartheta \iota \kappa \lambda \Lambda \mu \nu \xi \Xi \pi \Pi \varpi \rho \varrho \sigma \Sigma \varsigma \tau \upsilon \Upsilon \phi \Phi \varphi \chi \psi \Psi \Omega \omega\)

$\alpha \beta \gamma \Gamma \delta \Delta \epsilon \varepsilon \zeta \eta \theta \Theta \vartheta \iota \kappa \lambda \Lambda \mu \nu \xi \Xi \pi \Pi \varpi \rho \varrho \sigma \Sigma \varsigma \tau \upsilon \Upsilon \phi \Phi \varphi \chi \psi \Psi \Omega \omega$

显示	命令	显示	命令
\(\alpha\)	\alpha	\(\beta\)	\beta
\(\gamma\)	\gamma	\(\delta\)	\delta
\(\epsilon\)	\epsilon	\(\zeta\)	\zeta
\(\eta\)	\eta	\(\theta\)	\theta
\(\iota\)	\iota	\(\kappa\)	\kappa
\(\lambda\)	\lambda	\(\mu\)	\mu
\(\nu\)	\nu	\(\xi\)	\xi
\(\pi\)	\pi	\(\rho\)	\rho
\(\sigma\)	\sigma	\(\tau\)	\tau
\(\upsilon\)	\upsilon	\(\phi\)	\phi
\(\chi\)	\chi	\(\psi\)	\psi
\(\omega\)	\omega

\(\# \$ \%\&\_\{\}\)

$\# \$ \%\&\_\{\}$

\(\pm \times \div \mid\)

$\pm \times \div \mid$

\(\cdot \circ \ast \bigodot \bigotimes \leq \geq \neq \approx \equiv \sum \prod \coprod\)

$\cdot \circ \ast \bigodot \bigotimes \leq \geq \neq \approx \equiv \sum \prod \coprod$

\(\emptyset \in \notin \subset \supset \subseteq \supseteq \bigcap \bigcup \bigvee \bigwedge \biguplus \bigsqcup\)

$\emptyset \in \notin \subset \supset \subseteq \supseteq \bigcap \bigcup \bigvee \bigwedge \biguplus \bigsqcup$

\(\log \lg \ln\)

$\log \lg \ln$

\(\bot \angle 30^\circ \sin \cos \tan \cot \sec \csc\)

$\bot \angle 30^\circ \sin \cos \tan \cot \sec \csc$

\(y{\prime}x \int \iint \iiint \oint \lim \infty \nabla\)

$y{\prime}x \int \iint \iiint \oint \lim \infty \nabla$

\(\because \therefore \forall \exists\)

$\because \therefore \forall \exists$

\(\uparrow \downarrow \leftarrow \rightarrow \Uparrow \Downarrow \Leftarrow \Rightarrow \longleftarrow \longrightarrow \Longleftarrow \Longrightarrow\)

$\uparrow \downarrow \leftarrow \rightarrow \Uparrow \Downarrow \Leftarrow \Rightarrow \longleftarrow \longrightarrow \Longleftarrow \Longrightarrow$

\(\overline{a+b+c+d} \underline{a+b+c+d} \overbrace{a+\underbrace{b+c}_{1.0}+d}^{2.0} \hat{y} \check{y} \breve{y}\)

$\overline{a+b+c+d}
\underline{a+b+c+d}
\overbrace{a+\underbrace{b+c}_{1.0}+d}^{2.0}
\hat{y} \check{y} \breve{y}$

\( \begin{matrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{matrix} \)

$
\begin{matrix}
1&0&0\\
0&1&0\\
0&0&1\\
\end{matrix}
$

在起始、结束标记处用下列词替换 matrix
pmatrix ：小括号边框
bmatrix ：中括号边框
Bmatrix ：大括号边框
vmatrix ：单竖线边框
Vmatrix ：双竖线边框

\[\begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\ \end{bmatrix} \]

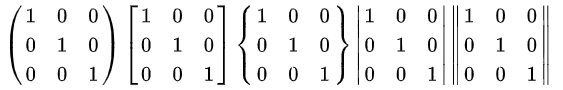
$$
\begin{bmatrix}
{a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\
{a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\
{\vdots}&{\vdots}&{\ddots}&{\vdots}\\
{a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\
\end{bmatrix}
$$

\[\begin{array}{c|lll} {↓}&{a}&{b}&{c}\\ \hline {R_1}&{c}&{b}&{a}\\ {R_2}&{b}&{c}&{c}\\ \end{array} \]

$$
\begin{array}{c|lll}
{↓}&{a}&{b}&{c}\\
\hline
{R_1}&{c}&{b}&{a}\\
{R_2}&{b}&{c}&{c}\\
\end{array}
$$

\[\begin{cases} a_1x+b_1y+c_1z=d_1\\ a_2x+b_2y+c_2z=d_2\\ a_3x+b_3y+c_3z=d_3\\ \end{cases} \]

$$
\begin{cases}
a_1x+b_1y+c_1z=d_1\\
a_2x+b_2y+c_2z=d_2\\
a_3x+b_3y+c_3z=d_3\\
\end{cases}
$$

https://www.jianshu.com/p/a0aa94ef8ab2
https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference
https://blog.csdn.net/xingxinmanong/article/details/78528791