unity Quaternion(四元数)与Transform
Transform
| 属性 | 说明 |
|---|---|
| Matrix4x4 localToWorldMatrix: | 本地坐标->世界坐标的矩阵信息。 |
| Matrix4x4 worldToLocalMatrix: | 世界坐标->本地坐标的矩阵信息。 |
| 方法 | 说明 |
|---|---|
| Vector3 TransformDirection(Vector3 direction): | 本地坐标->世界坐标,不受位置和缩放影响(只旋转坐标方向)。 |
| Vector3 TransformPoint(Vector3 position): | 本地坐标->世界坐标,受位置和缩放影响。 |
| Vector3 TransformVector(Vector3 vector): | 本地坐标->世界坐标,不受位置影响,受缩放影响。 |
| 方法 | 说明 |
|---|---|
| Vector3 InverseTransformDirection(Vector3 direction): | 世界坐标->本地坐标,不受位置和缩放影响(只旋转坐标方向)。 |
| Vector3 InverseTransformPoint(Vector3 position): | 世界坐标->本地坐标,受位置和缩放影响。 |
| Vector3 InverseTransformVector(Vector3 vector): | 世界坐标->本地坐标,不受位置影响,受缩放影响。 |
transform.position=new Vector3(10,0,0);
transform.eulerAngles=new Vector3(0,90,0);
transform.localScale=new Vector3(0.5f,0,0.5f);
Vector3 relative=transform.InverseTransformDirection(new Vector3(5,0,5));//转换结果见下图A
Debug.Log(relative);//output: (-5, 0, 5)
relative=transform.InverseTransformPoint(new Vector3(5,0,5));//转换结果见下图B
Debug.Log(relative);//output:(-10, 0, -10)
relative=transform.InverseTransformVector(new Vector3(5,0,5));//转换结果见下图C
Debug.Log(relative);//output:(-10, 0, 10)
图A:
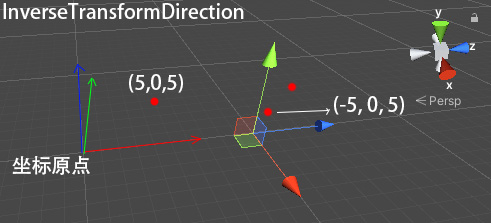
图B:

图C:

向量转换到Quaternion
public static Quaternion FromToRotation (Vector3 fromDirection, Vector3 toDirection);
Quaternion quaternion=Quaternion.FromToRotation(Vector3.right,new Vector3(1f,1f,0f));
Debug.Log(quaternion.eulerAngles);// output: (0.0, 0.0, 45.0)
public static Quaternion LookRotation (Vector3 forward, Vector3 upwards= Vector3.up);
Z 轴将与forward对齐,X 轴与 forward 和 upwards 之间的叉积对齐,Y 轴与 Z 和 X 之间的叉积对齐。如果 forward 或 upwards 量值为零,则返回恒等。如果 forward 和 upwards 共线,则返回恒等。
//将向量的方向转换为四元数
//x、y、z旋转角度都为0,就是Vector3.forward的方向
Quaternion qua0=new Quaternion();
Debug.Log(qua0.eulerAngles);//输出:(0.0, 0.0, 0.0)
//同上
Quaternion qua1=Quaternion.LookRotation(Vector3.forward);
Debug.Log(qua1.eulerAngles);//输出:(0.0, 0.0, 0.0)
//将向量Vector3.right的方向转换为四元数
Quaternion qua2=Quaternion.LookRotation(Vector3.right);
Debug.Log(qua2.eulerAngles);//输出: (0.0, 90.0, 0.0)
Quaternion qua3=Quaternion.LookRotation(Vector3.right,Vector3.forward);
Debug.Log(qua3.eulerAngles);//输出:(0.0, 90.0, 90.0) X向上,Y向前,Z向右
Quaternion qua4=Quaternion.LookRotation(Vector3.right,Vector3.right);
Debug.Log(qua4.eulerAngles);//输出:(0.0, 90.0, 0.0)
//向量(1,0,0)绕Y轴旋转90度。
Vector3 a=new Vector3(1,0,0);
Vector3 b=Quaternion.AngleAxis(90, Vector3.up)*a;
Debug.Log(b);//输出:(0.0, 0.0, -1.0)
//向量(1,1,0)旋转到Vector3.right的方向(左视图)
Vector3 e=new Vector3(1,1,0);
Vector3 f=Quaternion.LookRotation(Vector3.right)*e;
Debug.Log(f);//输出: (0.0, 1.0, -1.0)
//向量(1,1,1)旋转到Vector3.forward的方向(后视图)
Vector3 e=new Vector3(1,1,1);
Quaternion rotation=Quaternion.FromToRotation(e,Vector3.forward);
Vector3 f=rotation*e;
Debug.Log($"e.magnitude:{e.magnitude} f:({f.x}, {f.y}, {f.z})");
//输出:e.magnitude:1.732051 f:(-2.086163E-07, -2.086163E-07, 1.732051)
//相当于:e.magnitude:1.7 f:(0, 0, 1.7)
// 从平面的上方看向平面时,点在平面上的X,Y坐标
var plane=new Plane(Vector3.up,0);
var pos=new Vector3(2,0,3);
var rotation=Quaternion.FromToRotation(plane.normal,Vector3.back);
Vector3 pos2=rotation*pos;
//pos2.z=0; // z 不一定全等于0,会产生很小的小数
Debug.Log(pos2);//输出:(2.0, 3.0, 0.0)
// * 注意:此方法不一定正确,如下例并未得到向量 (1.0, 0.0, 0.0),旋转也出现意料之外的 z 轴 180
Vector3 planeNormal = Vector3.forward;
Quaternion rotation = Quaternion.FromToRotation(planeNormal, Vector3.back);
Debug.Log($"rotation:{rotation.eulerAngles}, {rotation * Vector3.left}");
// 输出: rotation:(0.0, 180.0, 180.0), (-1.0, 0.0, 0.0)
//将一个向量旋转到Transform组件的旋转角度
Vector3 f=new Vector3(0,0,1);
f=transform.rotation*f;//结果和transform.forward一样
Quaternion.LookRotation (Vector3 forward, Vector3 upwards= Vector3.up);
现在有两个对象,如下图:


梯子:旋转欧拉角度为x=0,y=90,z=22。
狗:旋转欧拉角度为x=0,y=0,z=0。
求狗爬上梯子时的旋转欧拉角?
var ladder=new GameObject();
ladder.transform.eulerAngles=new Vector3(0f,90f,22f);
Debug.Log(ladder.transform.up);//ouput:(0.0,0.9,0.4)
Debug.Log(ladder.transform.right);//ouput:(0.0,0.1,-0.9)
var rotation=Quaternion.LookRotation(ladder.transform.up,ladder.transform.right);
//dog.transform.rotation=rotation;
Debug.Log(rotation.eulerAngles);//output:(292,0.0,0.0)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号