向量积(外积、叉积、矢积、叉乘)

向量积，数学中又称外积、叉积，物理中称矢积、叉乘. 它的运算结果是一个向量而不是一个标量. 并且两个向量的叉积与这两个向量和垂直. 向量积可以被定义为：

$|\vec{a} \times \vec{b}|=|\vec{a}| \cdot|\vec{b}| \cdot \sin \theta$ 其中$\theta$是向量$\vec{a}$和$\vec{b}$的夹角.

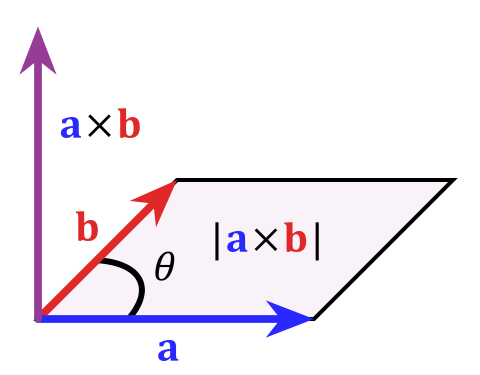
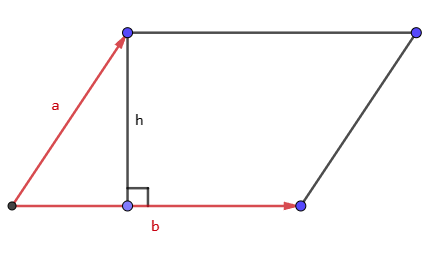
向量积的模的几何意义：\(|\vec{a} \times \vec{b}|\)表示了以\(\vec{a}\)和\(\vec b\)为边的平行四边形的面积

向量积的坐标表示：
对于给定向量\(\boldsymbol{\alpha}=\left\{a_1, a_2, a_6\right\}, \boldsymbol{\beta}=\left\{b_1, b_2, b_3\right\}\)，我们来讨论向量积的坐标表示，此时\(\alpha=a_1 \boldsymbol{i}+a_2 \boldsymbol{j}+a_3 \boldsymbol{k}, \boldsymbol{\beta}=b_1 \boldsymbol{i}+b_2 \boldsymbol{j}+b_3 \boldsymbol{k}\)，其中\(\boldsymbol{i}, \boldsymbol{j},\boldsymbol{k}\)为单位向量.

\(\begin{aligned} & i=\{1,0,0\}, \\ & j=\{0,1,0\}, \\ & k=\{0,0,1\} \end{aligned}\)

为了便于记忆，将上式写成行列式的形式

\(\boldsymbol{\alpha} \times \boldsymbol{\beta}=\left|\begin{array}{ll} a_2 & a_3 \\ b_2 & b_3 \end{array}\right| \boldsymbol{i}-\left|\begin{array}{ll} a_1 & a_3 \\ b_1 & b_3 \end{array}\right| \boldsymbol{j}+\left|\begin{array}{cc} a_1 & a_2 \\ b_1 & b_2 \end{array}\right| \boldsymbol{k}=\left|\begin{array}{ccc} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array}\right|\)