Learning Spread-out Local Feature Descriptors

论文Learning Spread-out Local Feature Descriptors

为什么介绍此文：引入了一种正则化手段，结合其他网络的损失函数，尤其是最新cvpr 2018的hardnet（Working hard to know your neighbor’s margins: Local descriptor learning loss），可以达到state-of-the-art。同时本文大量总结性工作也比较好（据以参考下面第3节），所以一同拿来分享，同时参考上一篇阅读也不错。代码：https://github.com/ColumbiaDVMM/Spread-out_Local_Feature_Descriptor 、 结合下一篇博客中的hardnet：https://github.com/ColumbiaDVMM/hardnet

1. 摘要

本文提出一个简单有力的正则化技术可以显著提高在学习特征描述子中的pairwise和triplet loss。这里就是不论是siamese还是triplet结构，输出是feature embedding时，该正则技术都管用。本文思想就是要充分利用特征空间，作者认为好的特征描述子应该足够“apread-out“到整个空间。就是说提取到的特征向量应该尽可能散开，可以理解是最大化类间距离，最小化类内距离。 受到均匀分布uniform distribution启发，这里使用正则项来最大化发散特征向量。展示了基于该正则项的triplet loss远远优于已有的欧式距离。作为拓展，该技术还可以被用来提高图像级别的feature embedding。

 

2.介绍

所以本文是以图像特征描述子出发的，没有涉及输出为概率情况。寻找正确匹配的挑战主要是图像块尺度、视角、光照等。因此学习到的descriptor应该：匹配块在描述子空间应该close，而不匹配块应该far-away。pairwise损失和triplet损失是最常用的损失。目前有许多工作例如smart sampling strategies和structured loss（L2-Net）来提升triplet loss。特别的，上一篇博客中的SNet,利用global loss来区分匹配和不匹配对距离的分布。这个方法避免了复杂采样策略的设计并且展示了含有outliers的训练鲁棒性。

global loss的成功促使探索描述子空间的特性，我们的主要思想是好的特征描述子应该充分spread out，充分利用子空间。所以引入的这个正则项可以在没有困难样本挖掘的情况下优于所有的欧式距离。

 

3. 背景

1）pairwise loss

输入为一对匹配或者不匹配的图像。

用的最多的pairwise loss即为contrastive loss，即对比损失函数：

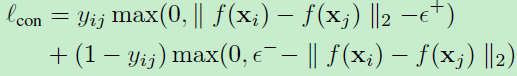
f(.)即为提取的特征向量，对比损失在lecun文章中最早提出，但是该函数容易过拟合，并且margin的选择非常关键。

2）Triplet loss

输入为a triplet of samples。常用的triplet loss为ranking loss：

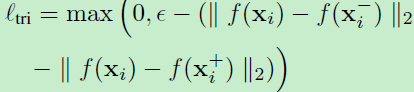
理想的ranking loss为分离匹配和不匹配样本的距离至少为margin。pairwise和triplet loss的主要不同是前者考虑匹配和非匹配图像的绝对距离，然而triplet loss考虑匹配和不匹配对的相对距离。所以一般triplet loss比pairwise loss在local descriptor learning中有更好表现。

3）Improvements

triplet loss和pairwise loss的主要问题是随着训练样本数目的增多，采样所有样本对、组变得不可行。而且只有相对一小部分样本可以有效被用来训练。正如实际观察到的，在很少的几个训练周期后，许多样本就会满足这一限制，训练变得没有效率。一个可能的解决方法是移除所谓的简易样本并且加入新的困难样本。然而决定哪些样本去移除或者添加是个难点【17，19】，此外仅仅关注不满足网络限制的样本太多会导致过拟合【17】。

【1】中tfeat提出一个提升版本的triplet loss，具体做法是在原损失函数中应用了困难负样本挖掘。思想是triplet中有两对图像是不匹配的，通过选择更加不匹配的那一图像对可挖掘相对更困难的样本。这称为anchor swap。【8】中提出的global loss并与传统的triplet loss结合用来解决在pairwise和triplet loss中的采样问题。global loss并没有考率采样问题，而是考虑一个batch中所有匹配和非匹配样本，并计算其距离的均值和方差。其主要思想是划分两个均值至一个margin，并最小化方差。作者认为这个方法有两个缺点：首先距离的分布不同的类差别可能很大，利用一个batch的样本来估计分布可能不够稳定。其次margin加入了额外的计算量。

结构化损失Structured loss【12，13，14，21，23】考虑所有匹配和非匹配对在一个batch中。通过小心设计loss 函数，结构化损失有能力关注困难样本。【14】提出lifted structured similarity softmax loss。【21】中的N-pair损失通过利用一个更高效的batch结构来实现。

本文的动机是好的描述子应充分利用整个描述子空间。文中提出的正则项来促进这种soread-out 特性。这个正则项很容易与其他损失结合，实验证明该正则项可以提高表现。

 

4. 方法

一种刻画spread-out的方法是：给定一个数据集，我们说学习到的描述子是spread-out的，如果任意两个随机采样的非匹配对是以很高概率近似正交的。作为一个很显然的例子，我们注意到均匀分布uniform distribution具有这个性质。为此作者提出两个命题，并给予了证明，这也是该正则项的数学来源。

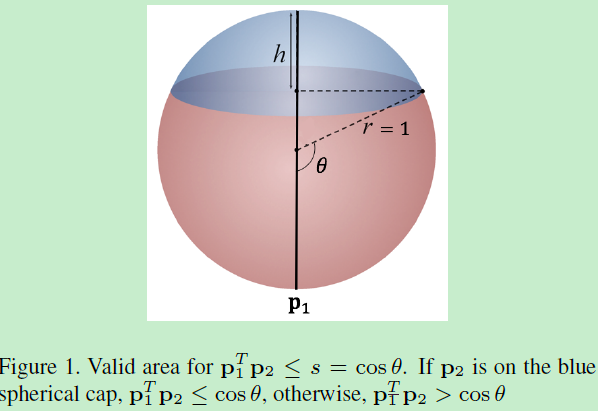
当p1和p2模为1时，其内积就等于p1p2 = conθ。

 

Proposition 1.

假定是从d维空间中的单位球面上均匀采样的两个独立点。每个点代表一个d维L2正则后的向量。那么内积的概率密度为：

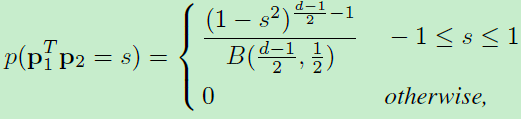        1）

其中分母B（a,b）为beta function。

证明： 这些d维空间中的向量都是被L2正则化后的，所以模为1，所以-1<=<=1,所以上式第二项的概率密度为0。为了求第一项的概率密度，我们可以首先计算累积分布函数CDF。因为CDF的导数即为概率密度函数PDF。这里仅考虑-1<=s<0的情况，因为0<=s<1相似。不失一般性，我们固定p1，并假定s=conθ，如图1。而cons函数在【0，pi】之间为单调函数，所以<=s当且仅当p2在图1中的蓝色球形。又因为p2在蓝色球形中均匀随机采样，所以<=s的概率等于蓝色球形占整个球形的比值。d-1维球形的区域面积为：

其中S0为整个球形面积，r=1为半径。h为蓝色球形的高，可以得出：h=r+rconsθ。I（）项为正则化的不完备（regularized incomplete）beta函数。因此将r、h带入上式得：

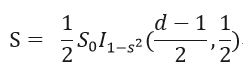
那么S0/S即为<=s的概率：

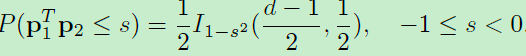
那么有了上面的累计概率分布，就可求导得到1）式中的概率密度函数了。

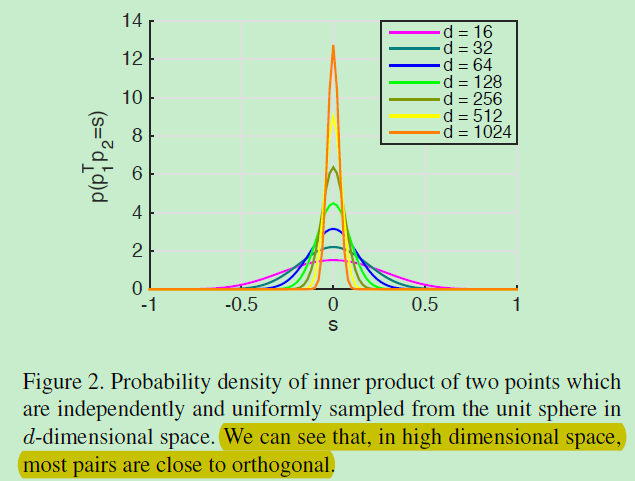
如图2，从d维空间中的单位球面均匀采样得到的两个点的内积的概率密度如上图，我们可以看到维数d越高，大多数图像对越近似于正交。基于上述观察，你可能希望使学习到的描述子匹配这种均匀分布。有两方面不可行，1)学习到的描述子的分布不仅取决于学习到的模型，还有图像本身（不可控）。2）技术上难以匹配这两个分布。相反，本文受此启发提出一种正则化技术，The regularization encourages the inner product of two randomly sampled non-matching descriptors matches that of two points independently and uniformly sampled from the unit sphere in its mean and second moment（从均值和第二力矩均匀采样）。
下面的命题展示了两个均匀采样的点，其均值和第二力矩分别为0和1/d。

 

Proposition 2.

假定是从d维空间中的单位球面上均匀采样的两个独立点。那么：

证明：

由于对称性，

 

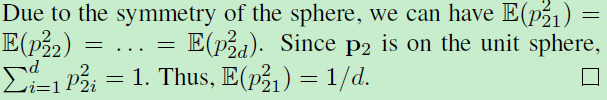
 Global orthogonal regularization（GOR）

 作者提出的正则化试图来匹配上面命题2中的均值和二阶矩。定义这种正则化为GOR（Global orthogonal regularization）。那么给定N个不匹配对，采样描述子的内积的均值为：

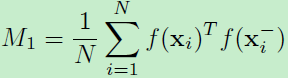
采样的内积二阶矩为：

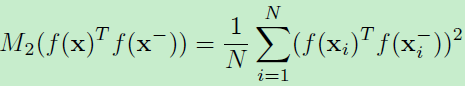
那么GOR定义为：

 

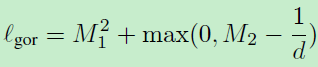
d为描述子的维度。看起来很简单，就是对非匹配对输出的特征向量进行了约束！而之前的global loss也是对特征向量的约束，只不过是对所有匹配非匹配样本！

同样也是在一个batch中来考虑这个约束，第二项约束是一个hinge loss形式，为么呢？因为多数非匹配样本早已满足这个约束，没有必要强制M2=1/d。为此作者对于第二项尝试了不同的loss，例如l1损失表现差不多，l2损失导致一点衰减。

这个正则性可以与任何损失函数一起使用：

在本文实验中，测试了GOR与对比损失函数、triplet loss、lifted structured similarity loss和N-pair loss一同使用的结果。

 

5. 实现

GOR是对于非匹配对、输出为feature embedding下的情况使用。同时这个feature向量是经过l2正则化的，以保证模为1。

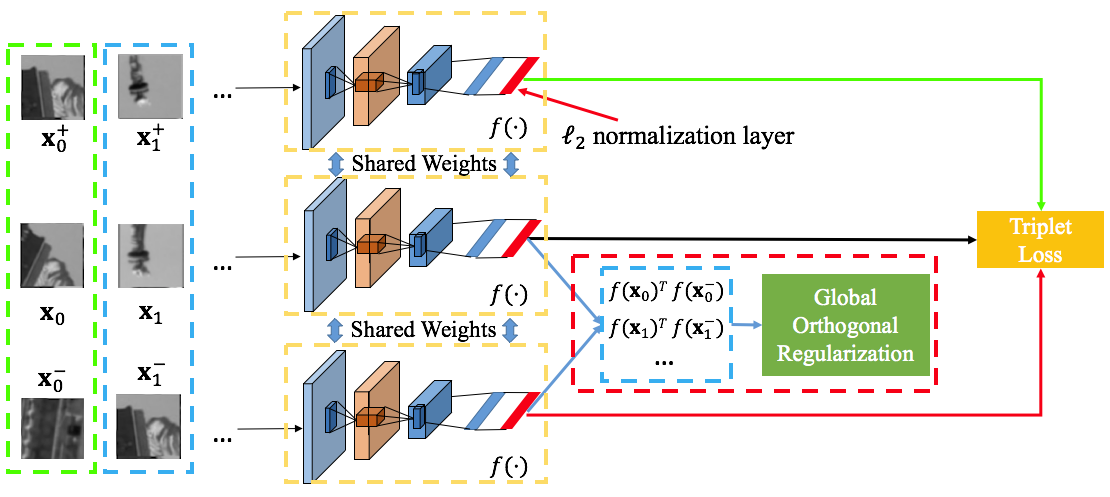
以下为结果，参数配置见论文。

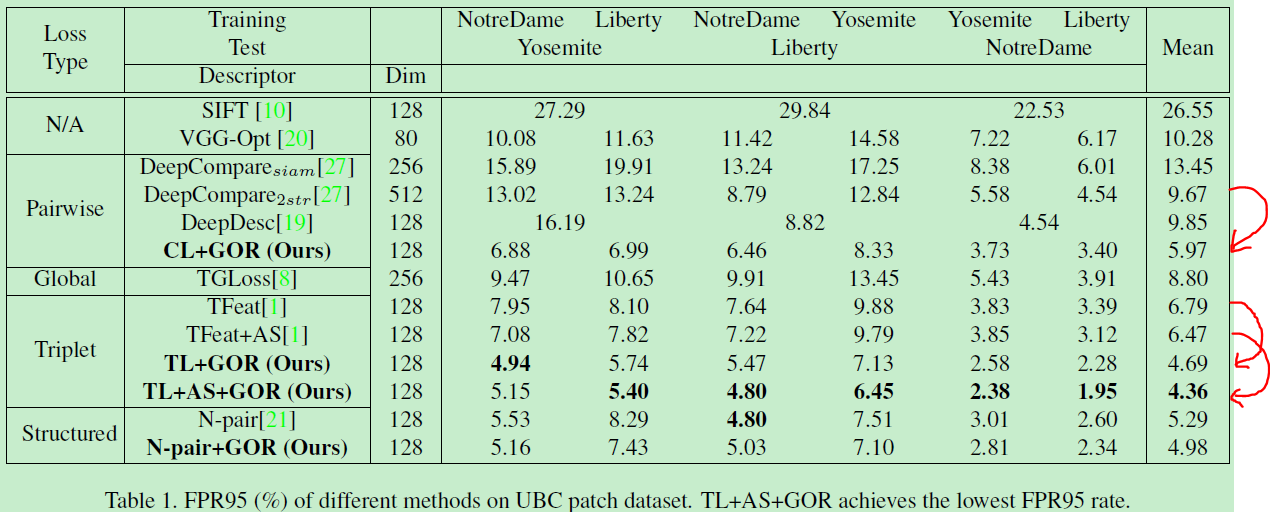
看出变化还是很大的，降了大约2个点左右。

 

看出加了GOR之后，两个分布更尖，方差变小。均值拉大。更易于区分。这个作用还是蛮像global loss的。

同时作者给出了feature embedding维数d=128最好，超参数alpha设为1。

源码：https://github.com/ColumbiaDVMM/Spread-out_Local_Feature_Descriptor

 

附：论文思想很像上一篇SNet，都是附加一个loss，global loss是对于输出不限制，可以是pairwise similarity和feature embedding，同时对匹配、非匹配都可以，损失类型都可以siamese或triplet。而gor loss对于输出限制为feature embedding，同时只作用于非匹配，损失类型不限。所以可集中实现这两个函数，做一个对比。