【论文阅读】TRO 2021: Fail-Safe Motion Planning for Online Verification of Autonomous Vehicles Using Convex Optimization

参考与前言

Last edited time: August 3, 2022 10:04 AM
Status: Reading
Type: TRO
Year: 2021
论文链接：https://ieeexplore.ieee.org/document/9302873

1. Motivation

safe motion planning对自动驾驶很重要，其中online verification 能保证自动驾驶车辆不会出现事故，但是现有的方法存在下列缺点：

  1. online verification并不高效，一般需要20HZ或更高的频率
  2. 在一些极端的情况下 全时间段内不能完全避免碰撞
  3. 在不安全场景，大多方法都缺少提供alternative motion plans

因聪明需要 所以总结了一下，感兴趣可看，大致了解一下无人车的规划相关工作

trajectory planning

discrete planning比较受欢迎，主要是离散化搜索空间、状态和输入空间等，motion primitives主要就是提前计算好轨迹快，然后通过search-based方案concatenaated到一起，这一步骤通常是offline的，所以可以应用于较为复杂的车辆模型，比如multibody modesl[19]

OS: 估计是将轨迹点预录下来的形式，或者建完图后有free的全局轨迹点 搜素空间

  • Sampling-based: RRT为主的，比较适合高维的搜索空间，但是由于随机采样，通常无法在时间内获得optimal motion
  • Graph-search: 比如state lattices，同属discrete planning。获取一系列轨迹，其goal states是预定义好的grid上的点，使用 lattice 结构表示。state lattices使用了优化来实现jerk-optimal。通常lattices能构建 可行驶的轨迹，但是 due to grid, it lack optimality and completeness

虽然discrete planning是比较容易实现并有效的解决motion问题的，但是缺点也很明显：也正是因为离散，所以可能在safety-critical scenarios with small and convoluted solution spaces 无法求解；同样的原因 也会导致在fail to determine trajectories ending in small safe terminal sets

故连续的model predictive control通过minimizing cost function 来生成无碰撞的轨迹，比如混合整数优化、sequential quadratic programs；因为求解的问题通常是非凸的，所以求解起来较为困难无法做到实时性；另一个则是可能造成local minimal

通常可以把非凸问题转成凸问题，比如线性化 vehicle dynamics，将motion分为横向和纵向的；[47]-[51] 说明了这一方法可以在全局收敛的情况下有效解决优化问题；但因为方法上分横纵，可能导致无法在复杂场景下获得可行轨迹。我们通过focusing on simple evasive maneuvers and providing safe fallback solutions来解决这一问题 → 对应Section VI.

safety verification

In theorem proving, desired system properties are formulated using logical formulas，然后verification步骤主要是checking the satisfiability of the logical formulas

如果从未进入inevitable collision states 则认为是安全的，ICS是一种状态：所有车辆自身可能的轨迹都会和障碍物相撞，ICS reason over infinite time horizons，在随机的交通场景 确定ICS是比较耗时的，大部分工作为提高效果，仅考虑其他参与者的一条轨迹。

为补充ICS，controlled invariant sets 保证了persistent feasibility，根据定义就是根据其他参与者，如果在CIS内的每个状态都存在一个无碰撞轨迹，则说明车辆是安全的。因为对障碍物未来状态的未知，计算CIS在动态环境中比较challenging

Set-based reachability analysis 通过计算所有的feasible轨迹，检查是否存在无碰撞轨迹；但是这一方法中，因为对未来所有的可能状态进行考虑，unsafe regions may grow rapidly。 导致的结果就是 刚规划的轨迹会被人为potentially unsafe，leaving AV without a safe trajectory. 在本篇文章中，我们通过结合fail-safe planning来结合reachable sets在verficiation中以解决这一问题

responsibility-sensible safety RSS 也是一种formal safety model

Contribution

主要贡献是展示了一种 verification technique 来保证车辆的安全性 弥补上面提到的以下不足，从上面抽取出来的：

  • 相关规划在方法上分横纵，可能导致无法在复杂场景下获得可行轨迹。本文通过focusing on simple evasive maneuvers and providing safe fallback solutions来解决这一问题 → 对应Section VI.
  • 计算CIS在动态环境中比较challenging
  • 因为对未来所有的可能状态进行考虑，unsafe regions may grow rapidly。 导致的结果就是 刚规划的轨迹会被人为potentially unsafe，leaving AV without a safe trajectory

2. Method

首先定义了问题，及 相关sets，这一部分有点多，建议看原文，主要是介绍所有变量的意义等，定义了set Z R^1 是自车的possible disturbances z，运动的微分公式为：

\[\begin{equation*} \dot{x}(t) = f\left(x(t),u(t),z(t)\right). \tag{1} \end{equation*} \]

使用 \(\chi\left(t_{h}, x\left(t_{0}\right), u\left(\left[t_{0}, t_{h}\right]\right)\right)\) 来表示 此公式的解，也就是满足motion下的轨迹集合

## 2.1 Invariably Safe Sets 计算

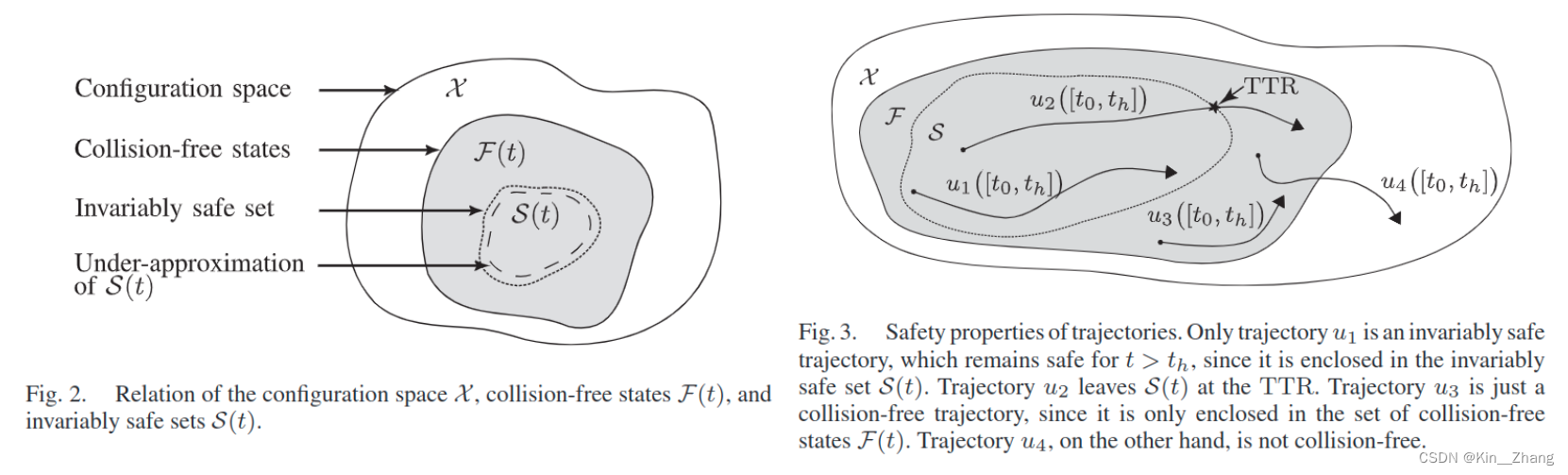
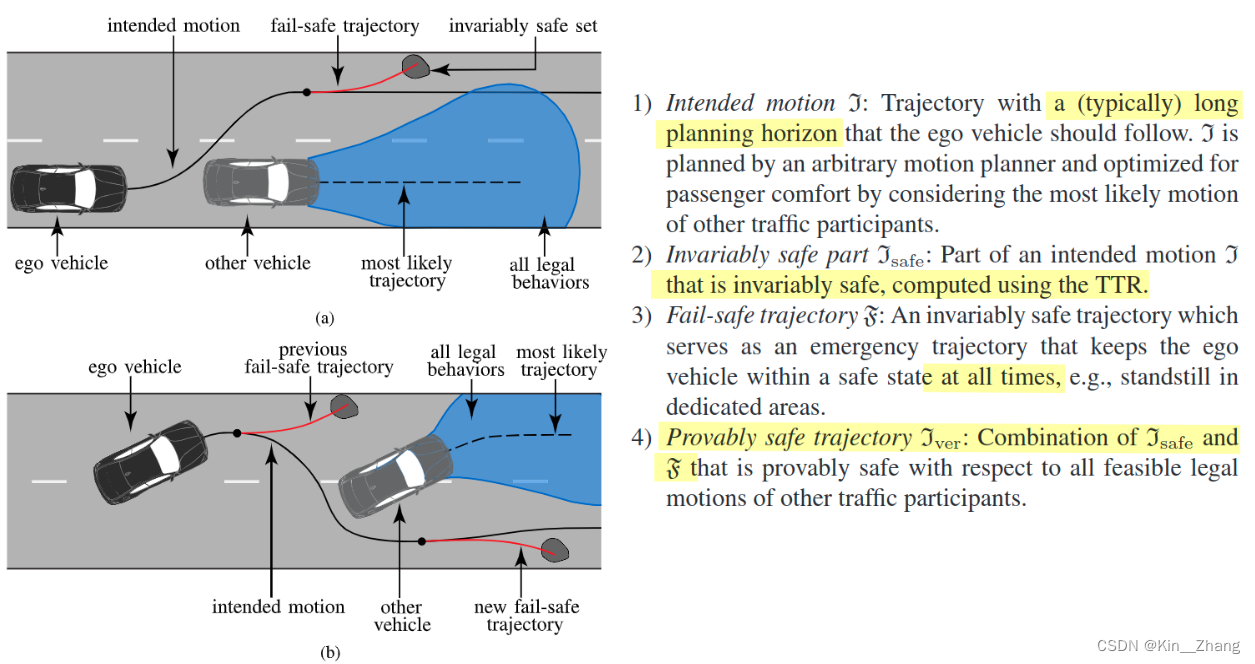
在他们之前的工作中有提到[68]，为计算 \(\mathcal S(t)\)，我们遵循一下规定：

  1. Formal safe distances[79]：不管前方车辆状态如何 包括前方车辆急刹等情况；在这个距离下，我们总是能刹停下来
  2. Evasive distances[80]：这个距离下 即使前方车辆急刹，我们也可以通过向相邻车道转向来避免碰撞

后面ab给我解释，两公式用了点时间，首先有个条件：

\[\begin{align*} & \left(|a_{\text{s,max,b}}| < |a_{\text{s,max}}| \right)\wedge \left(v^*_b < v_\text{ego} \right)\wedge\left(\frac{v_{\mathrm{ego}}}{|a_{\mathrm{s,max}}|} < \frac{v_b^*}{|a_{\mathrm{s,max,b}}|}\right), \tag{2} \end{align*} \]

如果满足这个条件，那么安全距离为：

\[\begin{align*} \Delta _{\mathrm{safe,1}}(v_{\mathrm{ego}},b):=&\frac{(v_b-|a_{\text{s,max,b}}|\delta _{\mathrm{brake}}-v_\text{ego})^2}{-2(|a_{\text{s,max,b}}|-|a_{\text{s,max}}|)}+v_\text{ego}\delta _{\mathrm{brake}}-v_b\delta _{\mathrm{brake}}+\frac{1}{2}|a_{\text{s,max,b}}|\delta _{\mathrm{brake}}^2\end{align*} \]

其中前面是一个整体 即\(\frac{(v-0)^2}{2a}\)；后面是另一个整体 在反应时间内的行驶相对距离 即 \(0+vt+\frac{1}{2}at^2\)

否则安全距离为： 即大家都以最大加速度减到速度为0的时候，外加一个自车的反应时间

\[\Delta _{\mathrm{safe,2}}(v_{\mathrm{ego}},b):=\frac{v_b^2}{-2|a_{\text{s,max,b}}|}-\frac{v_\text{ego}^2}{-2|a_{\text{s,max}}|} + v_\text{ego}\delta _{\mathrm{brake}}. \]

2.2 Safe& Evasive Distance Set

safe distance set

分横纵向考虑安全距离，纵向距离在[81,82] 二文中有详细考虑与证明：

\[\mathcal{S}^{1}(t)=\left\{(s, d, v)^{T} \in \mathcal{X} \mid \forall\left(s_{b}, d_{b}\right)^{T} \in \mathcal{O}_{b, \mathrm{cls}}(t): s \leq s_{b}-\Delta_{\mathrm{safe}, 2}(v, b)\right\} \]

而这里主要解释横向的evasive distance [感觉翻译成逃逸 逃离距离都不太好 所以就用原文把]，首先引入 \(d_{\mathrm{eva}}\) 作为车辆完全换道所需的横向距离，a为横向加速度

\[t_{\mathrm{eva}}:= \sqrt{\frac{2d_{\mathrm{eva}}}{a_{\mathrm{d,max}}}} + \delta _{\mathrm{steer}}\tag{5} \]

同时考虑前方车辆在这个时间内的行驶距离(纵)

\[\begin{split} \Delta s_b &:= v_bt_b-\frac{1}{2}|a_{\mathrm{s,max,b}}|t_b^2\\ t_b&:= \min (t_{\mathrm{eva}},\frac{v_b}{|a_{\mathrm{s,max,b}}|}). \end{split} \tag{6} \]

evasive distance set

定义如下，证明在[80]

\[\mathcal{S}^{2}(t)=\left\{(s, d, v)^{T} \in \mathcal{X} \mid \forall\left(s_{b}, d_{b}\right)^{T} \in \mathcal{O}_{b, \mathrm{cls}}(t): s \leq s_{b}-\Delta_{\text {eva }}^{t}(v, b)\right\} \]

Underapproximation of S

即前两者的set取并集，得到S

2.3 生成fail-safe Trajectories

纵向 Longitudinal Motion

首先是 纵向运动公式表示：\(x_{\text {lon }}=(s, v, a, j)^{T}\)，纵向距离、速度、加速度、jerk；我们使用加加速度作为input，将车辆纵向运动描述为linear time-invariant system

\[\begin{equation*} \frac{d^4}{dt^4}s(t)=u_{\mathrm{lon}}(t). \tag{8} \end{equation*} \]

然后加入约束，a 纵向前后的车辆距离，b 车辆本身的最大小 速度、加速度和jerk

\[\begin{align*} s_{\mathrm{min}}(t) \leq &x_{\mathrm{lon}}^{(0)}(t) \leq s_{\mathrm{max}}(t)\\ v_{\mathrm{min}}\leq &x_{\mathrm{lon}}^{(1)}(t) \leq v_{\mathrm{max}}\\ a_{\mathrm{min}}\leq &x_{\mathrm{lon}}^{(2)}(t) \leq a_{\mathrm{max}}\\ j_{\mathrm{min}}\leq &x_{\mathrm{lon}}^{(3)}(t) \leq j_{\mathrm{max}} \tag{10} \end{align*} \]

我们演示了刹车，但是因为是>0的加速度，所以此处我们引入两个deceleration limits \(a_{\min }<a_{\lim , 2}<a_{\lim , 1}<0\)，其中 \(\varsigma _{\mathrm{lon},1},\varsigma _{\mathrm{lon},2}\geq0\) 是slack variables 松弛约束 （JG: 优化的小trick 可以加速 更容易求解）

\[\begin{align*} x_{\mathrm{lon}}^{(2)}(t)&\geq a_{\mathrm{lim},1} - \varsigma _{\mathrm{lon},1}\\ x_{\mathrm{lon}}^{(2)}(t)&\geq a_{\mathrm{lim},2} - \varsigma _{\mathrm{lon},2}. \tag{11} \end{align*} \]

纵向的cost

\[\begin{align*} J_{\mathrm{lon}}\left(x(t),u(t)\right) =&\,w_ax_{\mathrm{lon}}^{(2)}(t)^2+w_jx_{\mathrm{lon}}^{(3)}(t)^2+w_{\varsigma _1}\varsigma _{\mathrm{lon},1}+w_{\varsigma _2}\varsigma _{\mathrm{lon},2}^2. \tag{12} \end{align*} \]

横向 Lateral Motion

同理 横向运动表示：\(x_{\text {lat }}=(d, \theta, \kappa, \dot{\kappa})^{T}\)，沿frenet坐标系下的离参考线的横向距离、orientation、曲率、自车曲率的变化

横向的运动描述为下列13公式，其中 \(u_{\mathrm{lat}}(t)=\ddot \kappa(t)\) 来源于 time-invariant linear

\[\begin{align*} \dot{x}_{\mathrm{lat}} =& \begin{pmatrix}0&v(t)&0&0\\ 0&0&v(t)&0\\ 0&0&0&1 \\ 0&0&0&0 \\ \end{pmatrix}x_{\mathrm{lat}}(t) + \begin{pmatrix}0\\ 0\\ 0\\ 1 \end{pmatrix}u_{\mathrm{lat}}(t)\\ &+ \begin{pmatrix}-v(t)\\ 0\\ 0\\ 0 \end{pmatrix}z_{\mathrm{lat}}(t). \tag{13} \end{align*} \]

对于collision free 将车辆看做三个圆，每个圆离参考线的距离可以用下列公式表示

\[\begin{equation*} d_i = d + \frac{i-1}{2}\ell \sin (\theta -\theta _\Gamma)\approx d+\frac{i-1}{2}\ell (\theta -\theta _\Gamma). \tag{14} \end{equation*} \]

再加上一系列的和纵向类似的约束，就不在此赘述了

横向的cost function：

\[\begin{equation*} \begin{split} J_{\mathrm{lat}}\left(x(t),u(t)\right) =&\,w_d x_{\mathrm{lat}}^{(0)}(t)^2+w_\theta \left(x_{\mathrm{lat}}^{(1)}(t)-\theta _\Gamma (t)\right)^2\\ &+w_\kappa x_{\mathrm{lat}}^{(2)}(t)^2+w_{\dot{\kappa }}x_{\mathrm{lat}}^{(3)}(t)^2. \end{split} \tag{18} \end{equation*} \]

生成Fail-Safe

首先是根据TTR生成初始状态，再由初始状态去计算接下来的fail-safe轨迹

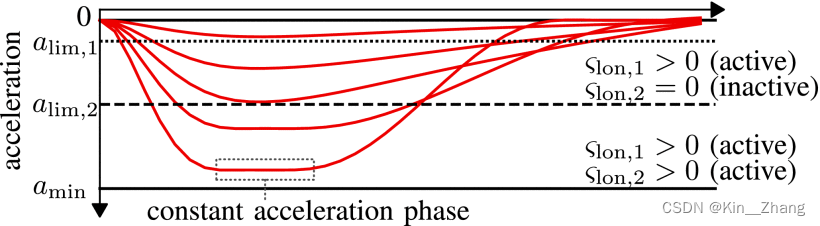
下列公式中 \(\Delta_{cor}\)为由车辆中心到后轴中心的距离修正项，\(s_{min}\leq s \leq s_{max}\)

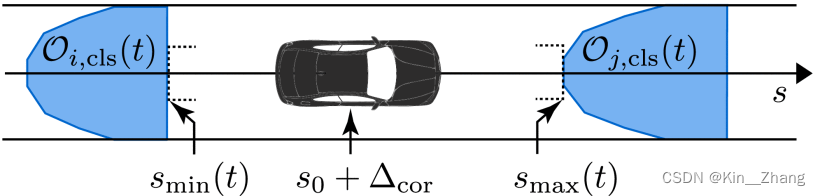
\[\begin{equation*} \begin{split} s_{\mathrm{min}}(t) = \sup \left\lbrace s-\Delta _{\mathrm{cor}}\,|\,\forall b \in \mathcal {B}_{\mathrm{fol}}: s-\Delta _{\mathrm{cor}}< s_0\right.\\ \left.\wedge (s,d)^T\in \mathcal {O}_{b,\mathrm{cls}}(t)\right\rbrace . \end{split} \tag{20} \end{equation*} \]

\[\begin{equation*} \begin{split} s_{\mathrm{max}}(t) = \inf \left\lbrace s-\Delta _{\mathrm{cor}}\,|\,\forall b \in \mathcal {B}_{\mathrm{pre}}:s-\Delta _{\mathrm{cor}}>s_0\right.\\ \wedge \left.(s,d)^T\in \mathcal {O}_{b,\mathrm{cls}}(t)\right\rbrace . \end{split} \tag{19} \end{equation*} \]

整体生成流程：

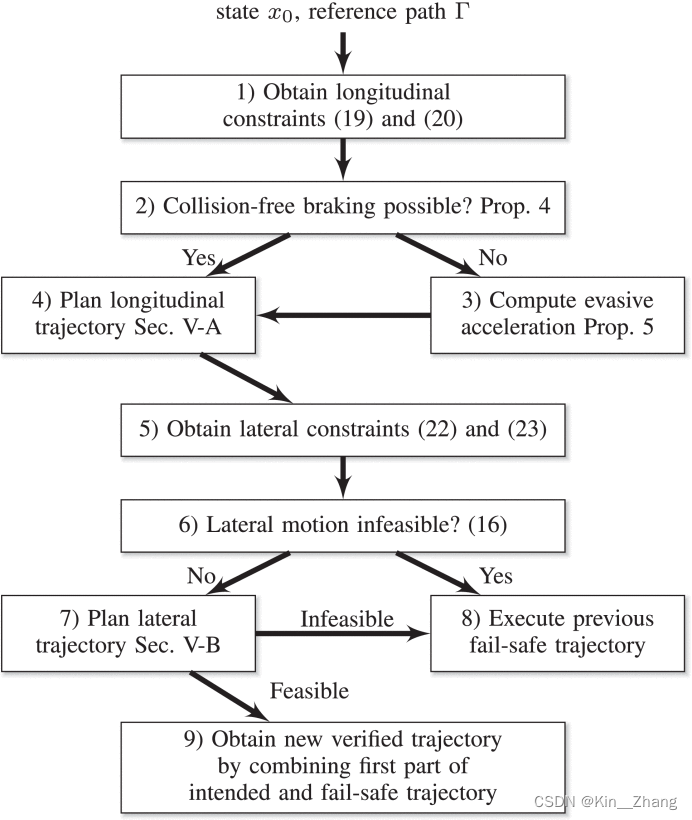
collision avoidance through braking

在初始状态下 能够紧急刹停的条件：Proposition 4

\[\begin{equation*} \begin{split} \forall t\in [t_0,t_h]: &\,s_0+v_0(\tau)-\frac{1}{2}|a_{\mathrm{max}}| \max (\tau -\delta _{\mathrm{brake}},0)^2 \\ &\leq s_{\mathrm{max}}(t), \tau :=\min (t,\frac{v_0}{|a_{\mathrm{max}}|}+\delta _{\mathrm{brake}}). \end{split} \end{equation*} \]

如果碰撞一定会发生，那么guaranteed Time-To-Collision是：

\[\begin{equation*} t_{\mathrm{GTTC}}:= \text{argmin}_{t\in [0,t_h]} \big |(s_0+v_0t) - s_{\mathrm{max}}(t)\big |. \end{equation*} \]

Evasice Acceleration可以由此表示：Proposition 5

\[\begin{equation*} a_{\mathrm{eva}}= \frac{2\left(d_{\mathrm{eva}}-|v_{\mathrm{lat}}|t_{\mathrm{GTTC}}\right)}{(t_{\mathrm{GTTC}}-\delta _{\mathrm{steer}})^2}. \end{equation*} \]

需要满足的距离曲线 示意

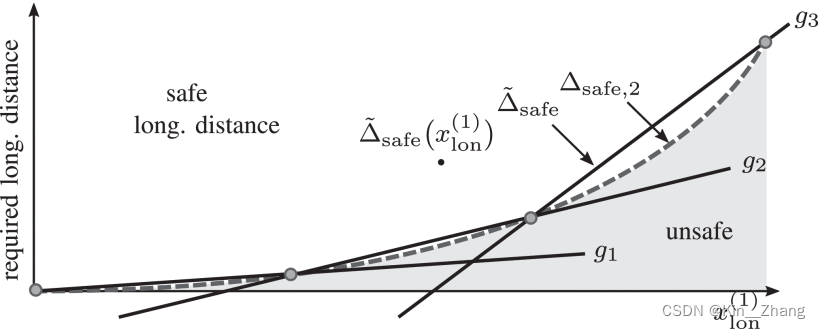
使用h段g的函数去近似安全距离 \(\Delta_{safe}\in\{\Delta_{safe,1},\Delta_{safe,2}\}\) 然后分速度区间去得到h段

为了将此加入到优化过程，可以表示为maximum function[88]

\[\begin{equation*} \tilde{\Delta }_{\mathrm{safe}}(x_{\mathrm{lon}}^{(1)}) = \max \left(g_1(x_{\mathrm{lon}}^{(1)}), g_2(x_{\mathrm{lon}}^{(1)}), \dots, g_h(x_{\mathrm{lon}}^{(1)})\right). \end{equation*} \]

然后加入纵向距离的约束中 公式(9)

\[\begin{align*} x_{\mathrm{lon}}^{(0)}(t) + \tilde{\Delta }_{\mathrm{safe}}(x_{\mathrm{lon}}^{(1)}) \leq s_{\mathrm{max}}(t). \tag{26} \end{align*} \]

因为求解器无法求解带max的函数，所以加入h个小于等于的约束, h不应该太大 也不能太小，前者会增加计算负担，后者会有较大误差

\[\begin{align*} x_{\mathrm{lon}}^{(0)}(t) + \left(g_{i}(x_{\mathrm{lon}}^{(1)})+\delta _{\mathrm{brake}}x_{\mathrm{lon}}^{(1)}\right) \leq s_{\mathrm{max}}(t). \tag{27} \end{align*} \]

3. 实验及结果

使用了Python和C++，优化求解库使用的是：CVXPY, ECOS and CVXPY-CODEGEN

Invariably safe set of the scenario

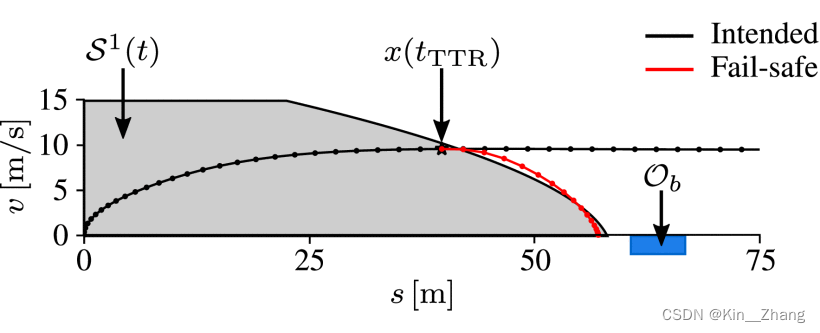
然后主要是实验了几个特定的场景 去验证 fail-safe 的轨迹运行情况：

静态障碍物、前方车辆急刹、行人冲出

4. Conclusion

提出了fail-safe motion planning 来保证AV不会发生事故

对比于其他的verification，我们的方法是第一个能在arbitrary traffic situations使用的；同时保证了40ms内的计算时间，可以与任何其他的motion plan相结合

我们的方案并不会使AV在过度的保守策略中

如果相关法规被扩展，我们的verification也可以自动适应。通过提供的occupancy sets来捕获其他交通参与者的所有合法行为

碎碎念

一开始，ab说这篇算是保守策略的，也就是考虑最差情况；但是初读的时候发现他们在摘要就说了 不会采取过度保守策略，后面一开始没get到这个点，直到问jg的时候发现slack variable和weights的一些trick设计，也就是并不是 非0即1 而是可以超过约束

对于fail-safe的概念也是先由TTR生成状态，然后根据流程图去判断纵向刹停是否可以，不可以的话换横向避障；整体算是一个求解优化问题，只是约束条件等由一系列的状态去决定

赠人点赞 手有余香 😆；正向回馈 才能更好开放记录 hhh

posted @ 2022-08-03 10:16  Kin_Zhang  阅读(355)  评论(0)  编辑  收藏  举报