【论文阅读】Optimization-Based Collision Avoidance
前言与参考
-
论文地址:https://ieeexplore.ieee.org/document/9062306
文章是2018年5月提出的,但是到了2020年才发表到ACC 所以时间轴上写的是2021年5月刊的ACC,算是近年来把凸优化来表示这个的开端(当然有更早的) 然后带起了一波热度的感觉。这篇文章自身也有 74cites了
我的主要是顺整个论文而不是只提取一个小部分... 虽然这样子干起来 套娃现象非常严重。基于优化的方法主要是:如何将碰撞问题转换成一个优化约束问题,然后用数值优化的方法去做求解。
基础知识
避障问题是一个NP-hard问题:
P问题、NP问题、NP完全问题和NP难问题 - 知乎 (zhihu.com)
也就是NP问题能约化到他,但是他并不是一个NP问题
I 介绍
对于基于优化计算轨迹的最大挑战在于:如何合适的表示collision avoidance,一般碰撞问题是非凸的并且很难进行求解。当然也有很多论文指出了应该怎样去求解这个碰撞问题
-
碰撞约束被近似成一个线性约束,但是很难去度量这个近似的误差 [10]
-
部分文章直接将这个问题下的机器人看做一个点物体,所以并不适用于多维度的机器人 比如机械臂
-
如果将障碍物看做多面体,那么碰撞约束通常会转成一个整数变量[16]
the discrete set Y corresponds to a polyhedral set of integer points, \(Y=\left\{y \mid y \in \boldsymbol{Z}^{m}, A y \leq a\right\}\), which in most applications is restricted to 0–1 values, \(y ∈ \{0, 1\}^m\).

[16] Grossmann, Ignacio E. "Review of nonlinear mixed-integer and disjunctive programming techniques." Optimization and engineering 3.3 (2002): 227-252.
所以以上这三种reformulation对于凸限制下的线性系统来说非常具有吸引力,因为在这样的条件下 混合整数优化问题可以被解决。一般来说当设计实时性系统时,整数变量应该避免在非线性系统中优化问题中出现
在本文中,我们主要研究:机器人在n维空间内避障运动,提出模型:建模避障问题约束,并避免之前说到的这三个问题出现
-
机器人和障碍物都描述成凸集,例如polytopes或ellipsoids(椭圆体) 然后碰撞问题就可以exactly and non conservatively reformulated 成一系列平滑的非凸限制
主要是使用strong duality of convex optimization在两个凸集间reformulating距离函数 -
还有第二种方法是建立在signed distance,也就是带符号的距离值,这样就能表达物体之间的交叉现象问题。这种情况下也能计算即使在要碰撞时 最小损坏程度的碰撞轨迹是怎样的
-
较难求解
-
杰哥:可能是和哪条边碰
吴院:也就是说在表达障碍物这件事上是整数约束给出的 因为渲染像素,mesh值等都不能切半(分辨率确定情况下);还有一些东西,比如说特征点的位置的优化,如果说是一定要在图像当中的像素的话,那就是一个整数规划问题,但是现在比如说VINS等等,都是用的浮点数去去去计算的,只是这样算出来的,对于图像来讲它没有意义。
参考16:离散集 Y 对应于整数点的多面体集
好像是M个障碍物,M整数约束在障碍物数量上
A. Related work
作者挺刚的,一上来就是:in this article, we do not review, or compare, optimization-based collision avoidance methods with alternative approaches, such as those based on xxx
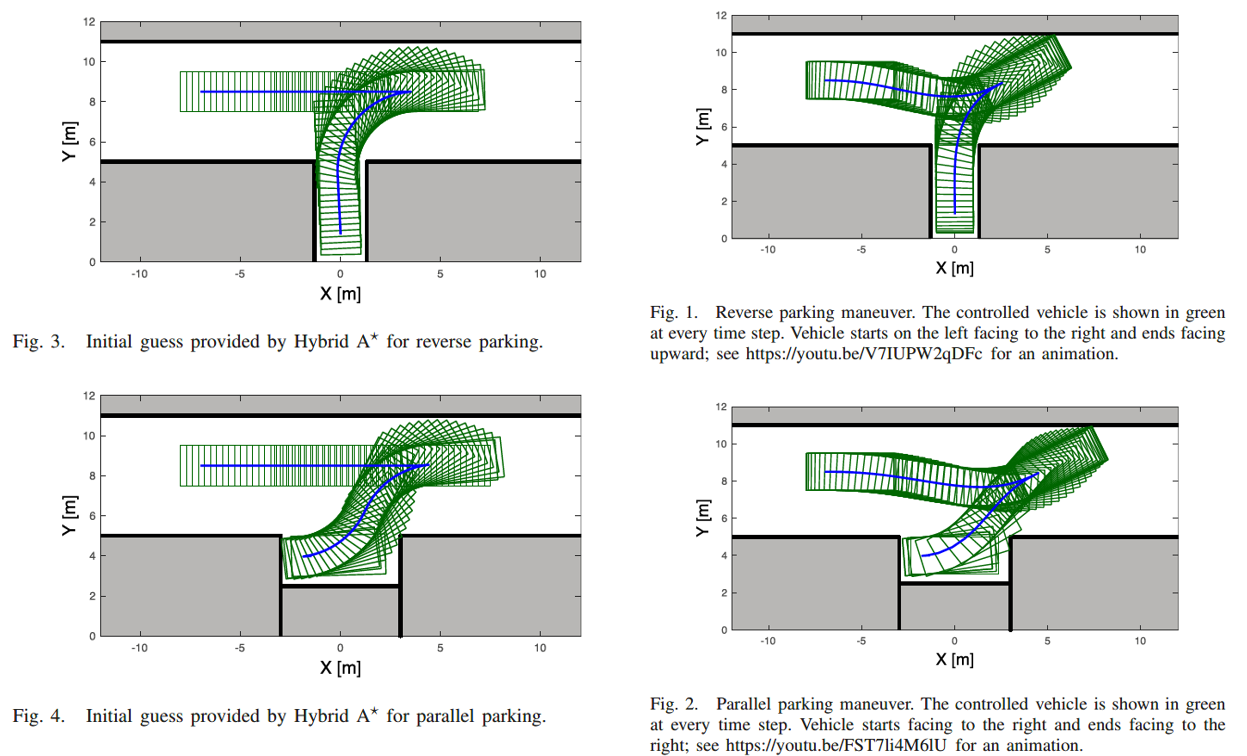
实际上在实验上也是如此,只是一开始说Hybrid A*太bangbang了,不像人开的一把倒车这种(虽然有时候人也不一定能一把倒好)。那就大致总结一下作者的看法:
- dynamic programming [17]
- reachability analysis [18]-[20]
- graph search method 比如A, Hybrid A [21]-[23]
- (random) sampling,比如急速随机探索的RRT和RRT* [24]-[27]
也就是以上几种都是作为基于优化的方法但是随同了一些其他方法,但是一般优化都需要一个warm start 肯定是需要随同其他给出一个呀 比如作者自己也是用了hybrid A*的warm start
从[29] 我们知道避障问题是一个已知的NP-hard问题,基本上所有的实用性方法都会有一些启发项的东西,而这些性能上的表现都是基于特定的问题和配置参数下,也就是泛化能力不强。
[30]-[34] 主要就是基于优化方法来考虑这一问题
II 问题描述
目标:找到一系列的控制指令使得机器人能从初始状态 \(x_s\) 运动到终点 \(x_F \in \mathbb R^{n_x}\)
- 同时优化我们的目标函数 \(J=\sum_{k=0}^{N} \ell\left(x_{k}, u_{k}\right)\) ,其中 \(\ell:\mathbb R^{n_x} \times \mathbb R^{n_u} \rightarrow \mathbb R\) 是一个stage cost
- 避免碰撞 \(M>1\) 个障碍物 \(\mathbb{O}^{(1)}, \mathbb{O}^{(2)}, \ldots, \mathbb{O}^{(M)} \subset \mathbb{R}^{n}\)
自身运动
状态间的转移:
- \(x_k \in \mathbb R^{n_x}\) 是指机器人初始状态 \(x_0=x_S\)在时间 \(k\) 时的状态,大多数时候这里的 \(x_k\) 表示的是位置 \(p_k\in \mathbb R^{n}\) 与角度 \(\theta_k \in \mathbb R^n\),当然也有速度 \(\dot p_k\) 和 角速度 \(\dot \theta_k\)
- \(u_k \in \mathbb R^{n_u}\) 是指控制输入
- \(f:\mathbb R^{n_x}\times \mathbb R^{n_u} \rightarrow \mathbb R^{n_x}\) 描述了系统的动力学
此文中假设没有噪音和扰动,那么系统受限于输入和状态:
自身空间内的表示:
- point-mass方式 自身就是一个小点 也就是位置点:
- full dimensional set方式 自身也是一个多边形表示 所以是在一个初始集上进行旋转平移
- 然后 \(\mathbb B\) 是一个多边形表示方式,"initial" convex set \(\mathbb B \subset \mathbb R^n\)
- 这个式子表示的是初始的一个多边形应该经过正阳的旋转和平移到自身的这样一个状态点 \(x_k\)
障碍物
多边形的表达方式,具体可以参照《凸优化》,其实多边形就是多条直线的交集,所以多边形就可以表达为如下,其中下面的 \(\mathcal K\) 是一种广义不等式的表达形式,可以简单理解为不等式就行。然后障碍物也是多边形,所以 \(\mathbb O\) 就认为是一个障碍物的表达式
其中 \(\preceq\) 在原文notation进行了一定的解释,不过就和上面说的将其理解成多条直线的交集即可。
结合上面公式,相关车体自身和障碍物的限制也就能表示出来了:
优化问题
结合公式(1)(2)(3),那么整体的优化问题就是这样的形式了:
其中 \(\mathbb{E}\left(x_{k}\right) \cap \mathbb{O}^{(m)}=\emptyset\) 通常情况下是一个非凸和不可微的约束。所以接下来我们会介绍两种novel的方法去建模这个碰撞问题使得其连续和可微,以便可以使用现有的off-the-shelf gradient或者是基于hassian的优化算法来求解。
III Collision Avoidance
首先介绍一下他人的工作比如这篇
[10] Schulman, John, et al. "Motion planning with sequential convex optimization and convex collision checking." The International Journal of Robotics Research 33.9 (2014): 1251-1270.
提出了如何formulating这个碰撞检测问题,基于他们提出来的signed distance
其中 \(\text {dist}(\cdot,\cdot)\) 和 \(\text {pen}(\cdot,\cdot)\) 公式如下:
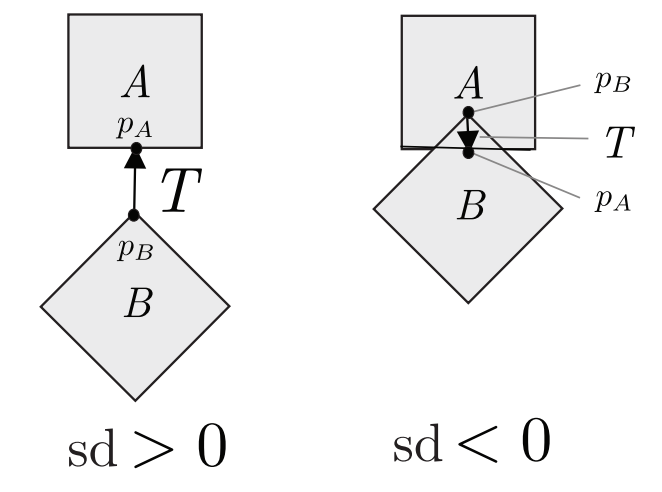
简单的来说就是sd>0的时候,他两不相交的最短距离值,sd<0时,则是他两相交的交集内的最短距离,可以大概结合一下上图看出来
所以这样子的情况下,我们的那个公式(3)的非凸和不可微的约束就可以换成 \(\text {sd}(\mathbb {E}(x), \mathbb O)>0\)。但是呢,问题还是存在的,还是非凸和不可微的;其次,为了让优化算法更有效求解,我们需要一个explicit的表达方式 但是 sd这种,本身就是dist 和pen这两个小的优化的最优解了。而这种情况下 我们会使用局部线性化近似(有空的话 再套娃看一下吧,这就是一开始介绍中说的 这样子方法的error是不好估计的。也就是说近似可以 但是你要知道近似的error这样好把控这个求解
本文提出的reformulation的方法就可以克服这个不可微问题 也不需要一个对于sd距离的explicit表达。虽然前文中提出的两种方法 其实是.. 一个用在point-mass,一个在full-dimensional 前者的更容易写,后者是用于实验,原理是一个原理
-
ybw:如果知道的话,可能可以用在膨胀 \(d_{min}\) ,比如如果这个error超过膨胀的限值 可能这个解我们就不相信
本文方法
根据前面表达的:
则我们的碰撞问题中dist表达,其中\(d_{min}\) 是自身设定的安全距离阈值
公式(14) 已经直接把解法给出了,实际的证明过程如下:
-
这是根据前面我们表达的自身和障碍物而的出来的求解式子:
\[\begin{align*}\operatorname{dist}(\mathbb{E}(x), \mathbb{O})&=\min _{e, o}\left\{\|e-o\|: A o \preceq_{\mathcal{K}} b, e \in \mathbb{E}(x)\right\}\\&=\min _{e^{\prime}, o}\left\{\left\|R(x) e^{\prime}+t(x)-o\right\|: A o \preceq_{\mathcal{K}} b, G e^{\prime} \preceq_{\overline{\mathcal{K}}} g\right\}\end{align*} \] -
对这个问题进行dual
\[\max _{\lambda, \mu}\left\{-g^{\top} \mu+(A t(x)-b)^{\top} \lambda: G^{\top} \mu+R(x)^{\top} A^{\top} \lambda=0,\left\|A^{\top} \lambda\right\|_{*} \leq 1, \lambda \succeq_{\mathcal{K}} 0, \mu \succeq_{\overline{\mathcal{K}}} \cdot 0\right\} \]-
详情推导展开
首先需要打开凸优化英文原版418页 页码402页

-
-
dual全部完成后 还是一个nonconvex的优化问题,但是满足KKT条件就可以引入数值优化求解的方法,类似于一种迭代?但是因为是这样的 所以需要一个warm start 而这个warm start很大程度上决定了你是否能找到较好的解。
\[\begin{align*}&\displaystyle \min _{\mathbf x, \mathbf u,\boldsymbol \lambda, \boldsymbol \mu } \displaystyle \quad \sum _{k=0}^{N} \ell (x_{k}, u_{k}) \\&\,\,\, \text {s.t.} \quad \,\,~~x_{0} = x(0),\quad x_{N+1} = x_{F} \\&\qquad \quad \,\,\,\,\,~ x_{k+1} = f(x_{k},u_{k}),\quad h(x_{k}, u_{k}) \leq 0 \\&\qquad \quad \,\,\,\,\,-g^\top \mu _{k}^{(m)}+(A^{(m)}\,t(x_{k}) - b^{(m)})^\top \lambda _{k}^{(m)} > 0 \\&\qquad \quad \,\,~~ G^\top \mu _{k}^{(m)} + R(x_{k})^\top {A^{(m)}}^\top \lambda _{k}^{(m)} =0 \\&\qquad \quad \,\,~~ \big \|{A^{(m)}}^\top \lambda _{k}^{(m)}\big \|_{*} \leq 1, \quad \lambda _{k}^{(m)}\succeq _{ \mathcal {K}^{*}}0,~ \mu _{k}^{(m)}\succeq _{\bar{\mathcal {K}} ^{*}}0 \\&\qquad \quad \,\,\,~~ \text {for } k=0,\ldots,N,\quad m=1,\ldots,M\tag{15}\end{align*} \]
后半段是加入了sd为负的情况,也就是如果一定要撞上的话 怎样撞 撞的比较轻:
其中 \(s_{k}^{(m)} \in \mathbb R_+\)是一个在时间\(k\)下的slack variable associated with obstacle \(\mathbb O^{(m)}\),\(\kappa \ge0\) is a weight factor that keeps the slack variable as small as possible.
所以这么看下来主要不是说把非凸问题转成一个凸问题,而是非凸+不可微 → 非凸,然后使用Lagrange dual formulation去做成dual问题后 用数值优化方法进行求解。最后数值优化求解实验环节放在代码部分讲解,比较好直接对应,代码是julia版的
IV 代码阅读
车辆动力学
车的动力学 阿克曼模型的:
下图为各个解释:
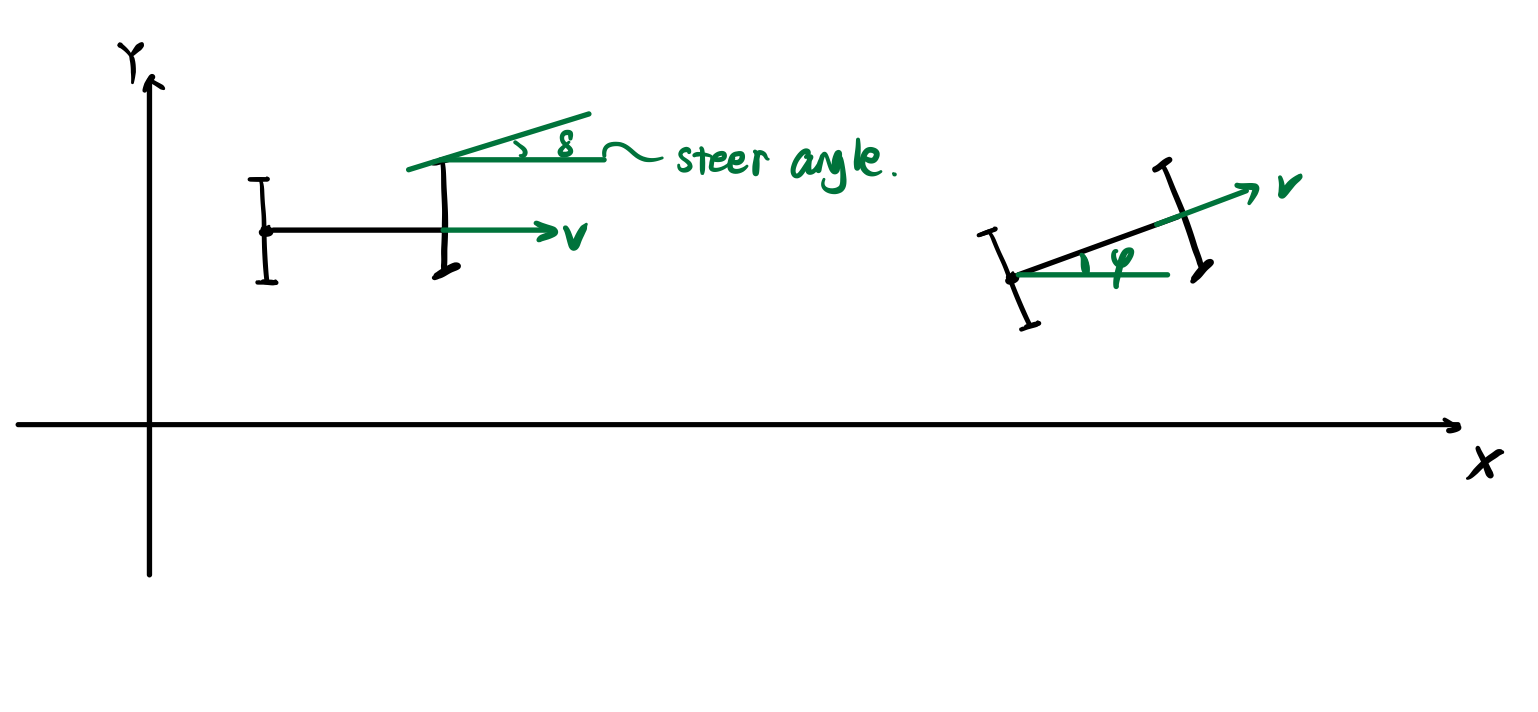
加上把这些范围对应到代码里
steering angle: \(\dot \delta \in [-0.6,0.6]\)
车辆速度:-1 到 2m/s
# [x_lower, x_upper, -y_lower, y_upper ]
XYbounds = [ -15, 15, 1, 10] # constraints are on (X,Y)
#input constraints
@constraint(m, [i=1:N], -0.6 <= u[1,i] <= 0.6)
@constraint(m, [i=1:N], -0.4 <= u[2,i] <= 0.4)
#state constraints
@constraint(m, [i=1:N+1], XYbounds[1] <= x[1,i] <= XYbounds[2])
@constraint(m, [i=1:N+1], XYbounds[3] <= x[2,i] <= XYbounds[4])
@constraint(m, [i=1:N+1], -1 <= x[4,i] <= 2)
##############################
# dynamics of the car
##############################
# - unicycle dynamic with euler forward
# - sampling time scaling, is identical over the horizon
for i in 1:N
if fixTime == 1
@NLconstraint(m, x[1,i+1] == x[1,i] + Ts*(x[4,i] + Ts/2*u[2,i])*cos((x[3,i] + Ts/2*x[4,i]*tan(u[1,i])/L)))
@NLconstraint(m, x[2,i+1] == x[2,i] + Ts*(x[4,i] + Ts/2*u[2,i])*sin((x[3,i] + Ts/2*x[4,i]*tan(u[1,i])/L)))
@NLconstraint(m, x[3,i+1] == x[3,i] + Ts*(x[4,i] + Ts/2*u[2,i])*tan(u[1,i])/L)
@NLconstraint(m, x[4,i+1] == x[4,i] + Ts*u[2,i])
else
@NLconstraint(m, x[1,i+1] == x[1,i] + timeScale[i]*Ts*(x[4,i] + timeScale[i]*Ts/2*u[2,i])*cos((x[3,i] + timeScale[i]*Ts/2*x[4,i]*tan(u[1,i])/L)))
@NLconstraint(m, x[2,i+1] == x[2,i] + timeScale[i]*Ts*(x[4,i] + timeScale[i]*Ts/2*u[2,i])*sin((x[3,i] + timeScale[i]*Ts/2*x[4,i]*tan(u[1,i])/L)))
@NLconstraint(m, x[3,i+1] == x[3,i] + timeScale[i]*Ts*(x[4,i] + timeScale[i]*Ts/2*u[2,i])*tan(u[1,i])/L)
@NLconstraint(m, x[4,i+1] == x[4,i] + timeScale[i]*Ts*u[2,i])
end
if fixTime == 0
@constraint(m, timeScale[i] == timeScale[i+1])
end
end
u0 = [0,0]
if fixTime == 1
for i in 1:N
if i==1
@constraint(m,-0.6<=(u0[1]-u[1,i])/Ts <= 0.6)
else
@constraint(m,-0.6<=(u[1,i-1]-u[1,i])/Ts <= 0.6)
end
end
else
for i in 1:N
if i==1
@NLconstraint(m,-0.6<=(u0[1]-u[1,i])/(timeScale[i]*Ts) <= 0.6)
else
@NLconstraint(m,-0.6<=(u[1,i-1]-u[1,i])/(timeScale[i]*Ts) <= 0.6)
end
end
end
cost function
最后cost function的形式是:
##############################
# cost function
##############################
# (min control inputs)+
# (min time)+
# (regularization dual variables)
u0 = [0,0]
#fix time objective
if fixTime == 1
@NLobjective(m, Min,sum(0.01*u[1,i]^2 + 0.5*u[2,i]^2 for i = 1:N) +
sum(0.1*((u[1,i+1]-u[1,i])/Ts)^2 + 0.1*((u[2,i+1]-u[2,i])/Ts)^2 for i = 1:N-1)+
(0.1*((u[1,1]-u0[1])/(Ts))^2 + 0.1*((u[2,1]-u0[2])/(Ts))^2) +
sum(0.0001*x[4,i]^2 for i=1:N+1)+
sum(0.001*(x[1,i]-rx[i])^2 + 0.001*(x[2,i]-ry[i])^2 + 0.01*(x[3,i]-ryaw[i])^2 for i=1:N+1))
else
#varo time objective
@NLobjective(m, Min,sum(0.01*u[1,i]^2 + 0.5*u[2,i]^2 for i = 1:N) +
sum(0.1*((u[1,i+1]-u[1,i])/(timeScale[i]*Ts))^2 + 0.1*((u[2,i+1]-u[2,i])/(timeScale[i]*Ts))^2 for i = 1:N-1) +
(0.1*((u[1,1]-u0[1]) /(timeScale[1]*Ts))^2 + 0.1*((u[2,1]-u0[2]) /(timeScale[1]*Ts))^2) +
sum(0.5*timeScale[i] + 1*timeScale[i]^2 for i = 1:N+1)+
sum(0.0001*x[4,i]^2 for i=1:N+1)+
sum(0.001*(x[1,i]-rx[i])^2 + 0.001*(x[2,i]-ry[i])^2 + 0.0001*(x[3,i]-ryaw[i])^2 for i=1:N+1) )
#
end
这里是两个形式为了简单解释 我们以fixTime那个 虽然我也不知道fix的是啥,似乎是离散的时间步长还不一样。
每个sum都对应了公式(20)
-
\(\sum _{k=0}^{N-1} u_{k}^\top R u_{k}\) ,其中 \(R=\text{diag}(0.01,0.5)\)
sum(0.01*u[1,i]^2 + 0.5*u[2,i]^2 for i = 1:N) -
\(\sum _{k=0}^{N-1}\Delta {u}_{k}^\top R_{\Delta } \Delta {u}_{k}\),其中 \(R_{\Delta }=\text{diag}(0.1,0.1)\)
sum(0.1*((u[1,i+1]-u[1,i])/Ts)^2 + 0.1*((u[2,i+1]-u[2,i])/Ts)^2 for i = 1:N-1) +(0.1*((u[1,1]-u0[1])/(Ts))^2 + 0.1*((u[2,1]-u0[2])/(Ts))^2) -
\(\sum _{k=0}^{N-1}\ell (x_{k}, u_{k})\) 应该是这个,然后对应的是公式 (19) 所有平方和相加,也就是\(\dot {X}, \dot {Y}, \dot {\varphi }, \dot {v}\)
\[\sum _{k=0}^{N-1}\ell (x_{k}, u_{k})=\sum _{k=0}^{N-1}(\Delta \dot X^2+\Delta \dot Y^2+\Delta \dot {\varphi }^2+ \dot {v}^2) \]sum(0.0001*x[4,i]^2 for i=1:N+1) + sum(0.001*(x[1,i]-rx[i])^2 + 0.001*(x[2,i]-ry[i])^2 + 0.01*(x[3,i]-ryaw[i])^2 for i=1:N+1)
碰撞约束
这一段的约束全都限制在公式 (15)/(18)中,注释中都详细标明了对应的约束公式简述:
##############################
# obstacle avoidance constraints
##############################
# width and length of ego set
W_ev = ego[2]+ego[4]
L_ev = ego[1]+ego[3]
g = [L_ev/2,W_ev/2,L_ev/2,W_ev/2]
# ofset from X-Y to the center of the ego set
offset = (ego[1]+ego[3])/2 - ego[3]
for i in 1:N+1 # iterate over time steps
for j = 1 : nOb # iterate over obstacles
Aj = A[sum(vOb[1:j-1])+1 : sum(vOb[1:j]) ,:] # extract obstacle matrix associated with j-th obstacle
lj = l[sum(vOb[1:j-1])+1 : sum(vOb[1:j]) ,:] # extract lambda dual variables associate j-th obstacle
nj = n[(j-1)*4+1:j*4 ,:] # extract mu dual variables associated with j-th obstacle
bj = b[sum(vOb[1:j-1])+1 : sum(vOb[1:j])] # extract obstacle matrix associated with j-th obstacle
# norm(A'*lambda) <= 1
@NLconstraint(m, (sum(Aj[k,1]*lj[k,i] for k = 1 : vOb[j]))^2 + (sum(Aj[k,2]*lj[k,i] for k = 1 : vOb[j]))^2 <= 1 )
# G'*mu + R'*A*lambda = 0
@NLconstraint(m, (nj[1,i] - nj[3,i]) + cos(x[3,i])*sum(Aj[k,1]*lj[k,i] for k = 1:vOb[j]) + sin(x[3,i])*sum(Aj[k,2]lj[k,i] for k = 1:vOb[j]) == 0 )
@NLconstraint(m, (nj[2,i] - nj[4,i]) - sin(x[3,i])*sum(Aj[k,1]*lj[k,i] for k = 1:vOb[j]) + cos(x[3,i])*sum(Aj[k,2]lj[k,i] for k = 1:vOb[j]) == 0 )
# -g'*mu + (A*t - b)*lambda > 0
@NLconstraint(m, (-sum(g[k]*nj[k,i] for k = 1:4) + (x[1,i]+cos(x[3,i])*offset)*sum(Aj[k,1]*lj[k,i] for k = 1:vOb[j])
+ (x[2,i]+sin(x[3,i])*offset)*sum(Aj[k,2]*lj[k,i] for k=1:vOb[j]) - sum(bj[k]*lj[k,i] for k=1:vOb[j])) >= dmin )
end
end
然后就是使用IPOPT求解的过程了,其中有关于两个Lagrange factor的 warm start 求解过程一个initial