【路径规划】 Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame (附python代码实例)

参考与前言

---

1. 2010年，论文 Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame 地址：https://www.researchgate.net/publication/224156269_Optimal_Trajectory_Generation_for_Dynamic_Street_Scenarios_in_a_Frenet_Frame
2. Python代码示意地址：https://gitee.com/mirrors/PythonRobotics/tree/master/PathPlanning/FrenetOptimalTrajectory
3. csdn上matlab解释：https://blog.csdn.net/caokaifa/article/details/108015374
4. 格式更好看的notion外链版：https://www.notion.so/kinzhang/Frenet-Optimal-Trajectory-Generation-96d5bced98c146d2a9036a1d5fc2b21d
   后续更新也主要在notion上

主要是自己一直听过这个frenet的规划... 但是一直没了解到底是个啥，趁着这次杰哥的指点，顺便套娃一下基础知识好了。关于规划的使用中，19年的时候做二维grid map 小小圆盘二轮车用的Dijkstra/A*做的全局，然后局部是DWA（但是当时实验时车子总是蛇皮走位）照现在的感觉应该是膨胀系数给大了，DWA更新快了？然后路径规划完哎往墙走，哎躲个墙，哎再往墙走，就这种蛇皮 emmm 这么说好像还是不是很清楚原因，放着万一啥时候想通了呢 hhhh。这次这个主要是基础系列补... 补... 补

基础知识

---

因为基础补充，所以就... 慢慢来了，就当把自己的理解总结一下好了..

Frenet坐标系

首先是关于这个坐标系的，一般呢我们用的是笛卡尔坐标系（大白话 xy坐标轴），然后这个的不同之处就是按照你的那个车的路径定的，纵向距离叫s，横向距离叫d。例如此手画图：[这里的横纵是指车子在开的方向，车头前方是纵，方向盘的就是横]

python代码运行示意

• 所以这个在一开始定全局路径规划线的时候就是定frenet坐标系的时候嘛？中途还会有变化嘛？

  中途会有变换，比如这里提到的换道等..

感觉这个在生成轨迹后的切换方面很舒服噢

SO(2)和SE(2)

来源：《现代机器人学》

也就是说SO是只关注于对比的旋转，SE添加了向量坐标的变换

论文部分

---

摘要 Abstract

主要是为了解决高速公路的动态规划问题，同时对于市中心交通堵塞问题下的自动驾驶车的轨迹要求等。提出了 semi-reactive 轨迹生成方法，是结合了行为规划层的一种方法。方法上实现了在常规街道 使用Frenet坐标系采用最优控制策略以使得车辆能够实现速度保持、汇入车道、跟车、停车、反应式避障等的长期目标

看上去感觉就像... emmm 实现了基本无人小车的功能？可能多列举出来以行为动作形式展现

• semi-reactive是什么意思？怎么体现的？

  就是对周围物体能做交互，做出反应

介绍 Introduction

Motivation : 现有的方法(DAPRA 2007里提出的 18 heuristics and conservative estimates)没办法在交通堵塞和高速公路上提供好的表现，所以需要引入轨迹，更清楚的解释在时间t的规划和控制决策；方法主要是生成速度不变运动，然后再把速度和距离控制发到规划(planning)

Contributions : 策略上耦合了规划里面的反馈，这样可以更好将 导航任务层 分子任务到 实时的轨迹运行中，随后稳定由轨迹给出的跟踪响应控制；对比与其他方法由系统观测闭环控制，本文的方法主要在生成轨迹阶段

• [18] heuristics and conservative estimates 这个是啥方法？

• velocity invariant movement

  虽然在后面的注释中有，但是... 我还是看不懂这个注释表达的velocity invariant movement是什么：It is highly desirable to generate lane change and merging maneuvers, which are timed completely independently from the absolute travelling speed.

方法 Methods

最优控制方法 Optimal Control Approach

首先将最优控制理论应用到轨迹生成方面的工作，有很多人提出了[13] [3]。而我们的工作主要是确保一旦找到这个最优轨迹，使用Bellman's 优化原则去保持住，也就是在每一步都跟随之前定好的最优轨迹

相反的有些工作是直接拿样条曲线去做轨迹拟合，然后主要去满足一些确定的限制，优化问题的形式主要针对于曲线参数的选择，但是这种方法下的缺点比较明显，容易超调甚至是不稳定，比如这样

在最优控制方面，我们主要是遵循Bellman的最优化原则去选取cost function，轨迹在最小化cost的基础上也能最大程度的接近车辆理想的开车形式

对于理想的开车形式定义：假设车辆有明确的关于离期望轨迹的横向offset，在最初的变道或避障后应该要能返回原来的最优轨迹，权衡一些指标等去实现这一点

1. compromise: 如果车辆距前车快行/减速，应慢慢减速下来而不是急刹
2. ease and comfort: 这一点在数学上我们用jerk来指明，也就是加速度的导数，加速度随时间变化的程度
3. need time: 就是从起点到终点的时长

总的来说通用的限制优化问题不会受限于车辆场景变化，能在数值上求最优，但是问题总的来说复杂。而我们的方法给这个限制优化问题提供了合理的假设，然后得到一系列的优化解给到无限制的优化问题上，在这上面取满足限制条件的解

• 这里的保持住是指什么？也就是在每一步都跟随之前定好的最优轨迹
• 这里没有具体说明接近车辆理想的开车形式的方式吧，就算用了Bellman的最优化原则去选取，怎么能约束desired traffic behaviour？
• 可能得套娃一下Bellman's principle of optimality
• function class是啥个意思？
• emmm 给到 unrestricted (free) optimization problem但是后面又是fulfills the restrictions不会矛盾嘛？

Frenet坐标系下的Motion Planning

在跟踪控制理论比较好用的方法是：Frenet坐标方法，他能在 \(S E(2):=S O(2) \times \mathbb{R}^{2}\) 特殊欧式子群里有很好的跟踪性能(invariant tracking performance)

本文中在这种方法去结合横向和纵向cost function以适应不同的场景去模仿人的开车行为，首先整体的图如下。移动的参考坐标系由那一点的切向量 \(\vec{t}_{r}\) 和法向量 \(\vec{n}_{r}\) 来给出，其中左边的center line是指在无障碍物空旷道路的理想轨迹

先对比于直接在笛卡尔坐标系中生成轨迹，本文主要是在这个动态的参考系下对于 在center line的 \(\vec{r}\) 点和垂直offset距离是\(d\) 的轨迹 寻找一维的轨迹，这两者的关系式为

\[\vec{x}(s(t), d(t))=\vec{r}(s(t))+d(t) \vec{n}_{r}(s(t)) \tag{1} \]

对于人类感知中我们也存在对纵向和横向加速度变换的不同重视程度。因为上面的切向量和法向量变换比较快，所以我们就用前文提到的jerk \(s, d\) 来进行约束。五次多项式是用jerk-optimal 来连接 初始状态\(P_{0}=\left[p_{0}, \dot{p}_{0}, \ddot{p}_{0}\right]\) 和 结束状态 \(P_{1}=\left[p_{1}, \dot{p}_{1}, \ddot{p}_{1}\right]\) 之间的一维求解问题，更准确的说是 最小化在时间内最小化jerk平方的cost function

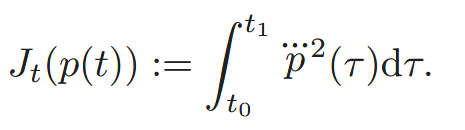
这里进行了一个证明：在给定初始状态和结束状态，求解下面这个最小cost functional的结果也是一个五次多项式

\[C=k_{j} J_{t}+k_{t} g(T)+k_{p} h\left(p_{1}\right) \]

其中 \(g\) 和 \(h\) 是随机的函数，\(k_j,k_t,k_p>0\)

• invariant tracking performance这个是其他什么跟踪性能指标吗？不变性？是指稳定性嘛？

• 具体为什么能在frenet坐标系下 跟踪控制理论好用呢？好像没有证明？

  看完横纵向大概知道了，因为对于求导速度的处理来说都很方便，这个没有什么数值上的证明，就是方法上的便捷性吧

• 这里的表示？公式 感觉怪怪的

  是以center line作为坐标系原点，因为只有法向量方向发生改变所以是加上法向量的，然后带上他现在的方向上

• quintic polynomials are the jerk-optimal connection between x and x，这个connection是指？五次多项式的本质嘛

• 感觉这一块没有讲清楚frenet坐标系下的Motion planning问题啊... 主要在于限制条件太单一，只有最小化jerk function

  然后再代入计算cd和cv的最小

横向运动 Lateral Movement

高速下轨迹

因为要最小化这个jerk平方 在优化时我们在轨迹 \(s\) 中，我们选取最初状态为\(D_{0}=\left[d_{0}, \dot{d}_{0}, \ddot{d}_{0}\right]\)从后面部分，可知没有不连续的情况发生。对于优化本身来说，我们令\(\dot d_1=\ddot d_1=0\)，因为我们期望是能平行于center line的，接着确认 \(g(T)=T\) 和 \(h(d_1)=d_1^2\) 得到以下cos functional:

\[C_{d}=k_{j} J_{t}(d(t))+k_{t} T+k_{d} d_{1}^{2} \tag{2} \]

对于偏离center \(d=0\) 的我们需要加惩罚并使其慢慢收敛到求解，通过前面我们知道最优解是五次多项式，所以我们只需求出五次多项式的各个参数即可，然后最小化(2)中的 \(T\) ，最后检查碰撞

相对比于直接显式的计算最优轨迹然后再调整其系数，我们在第一步仿照[16] 整个轨迹是结合不同的结束状态 \(d_i\) 和 \(T_j\) 来计算多条的，又因为前面的得出求导=0，对于多项式的求解中的状态空间就变成了这样

\[\left[d_{1}, \dot{d}_{1}, \ddot{d}_{1}, T\right]_{i j}=\left[d_{i}, 0,0, T_{j}\right] \]

得出这上面的这么多条轨迹后，我们再取最小的那个cost。因为每一步我们都取的是最优解，那么剩下的每一个时间点也都会是最优解。那么整条轨迹就是最优的了

低速下轨迹

因为在高速下，可以认为 \(d(t)\) 和 \(s(t)\) 是独立的，但是在低速下，这样的假设忽略了车辆的non-holonomic性质，所以就算按照上面生成了最优轨迹也没法被车辆所执行 曲率不达标，在这样的情况下，我们将行为层换成了有速度阈值到考虑横向的同时也考虑纵向运动

• 所以实际的计算是 多条轨迹，然后计算每条轨迹cost 选一条？
• 这个non-holonomic性质体现在哪里？

纵向运动 Longitudinal Movement

不同于前面我们将时间/距离作为主要的评判标准，此处的评判标注主要是comfort和safety，所以我们引入了纵向的jerk 作为优化问题的考虑

因为保持距离，汇入车道和停车都是对于轨迹的特定未知的要求，也就是从现在状态转到纵向位置的变换 \(s_{target}(t)\) ，类似于横向的 我们生成纵向的轨迹，从\(S_0=[s_0,\dot s_0,\ddot s_0]\) 到通过差分 \(\Delta s_i\) 和 \(T_j\) 得到结束状态

\[\left[s_{1}, \dot{s}_{1}, \ddot{s}_{1}, T\right]_{i j}=\left[\left[s_{\text {target }}\left(T_{j}\right)+\Delta s_{i}\right], \dot{s}_{\text {target }}\left(T_{j}\right), \ddot{s}_{\text {target }}\left(T_{j}\right), T_{j}\right] \]

得出来的图如下，最后每条轨迹通过cost function进行计算：

\[C_{t}=k_{j} J_{t}+k_{t} T+k_{s}\left[s_{1}-s_{d}\right]^{2} \]

Following

安全跟车操作，安全距离也就是constant time gap law，所以车辆的立项s状态就是：

\[s_{\text {target }}(t):=s_{l v}(t)-\left[D_{0}+\tau \dot{s}_{l v}(t)\right] \]

• 其中\(D_0\) 和 \(\tau\) 都是常数项
• \(s_{lv}\)和速度\(\dot s_{lv}\) 都是前车的位置和速度

其中前车的一些数据都是需要通过感知预测来获得的，其中我们假设前车的加速度保持不变，\(\ddot{s}_{l v}(t)=\ddot{s}_{l v}\left(t_{0}\right)=\text { const. }\)

根据时间整合，关于前车的一些公式：

\[\begin{aligned}\dot{s}_{l v}(t) &=\dot{s}_{l v}\left(t_{0}\right)+\ddot{s}_{l v}\left(t_{0}\right)\left[t-t_{0}\right] \\s_{l v}(t) &=s_{l v}\left(t_{0}\right)+\dot{s}_{l v}\left(t_{0}\right)\left[t-t_{0}\right]+\frac{1}{2} \ddot{s}_{l v}\left(t_{0}\right)\left[t-t_{0}\right]^{2}\end{aligned} \]

然后时间求导，自身状态的变换：

\[\begin{aligned}&\dot{s}_{\text {target }}(t)=\dot{s}_{l v}(t)-\tau \ddot{s}_{l v}(t) \\&\ddot{s}_{\text {target }}(t)=\ddot{s}_{l v}\left(t_{1}\right)-\tau {s}^{'''}_{l v}(t)=\ddot{s}_{l v}\left(t_{1}\right) .\end{aligned} \]

Merging and Stopping

此项为汇入车道和停车操作。根据上面的一系列分析，这个就比较好定了，首先我们的目标点位置：

\[s_{\text {target }}(t)=\frac{1}{2}\left[s_{a}(t)+s_{b}(t)\right] \]

Velocity Keeping

速度跟随，主要是针对前方没有车的场景，车辆的目的就应该不是去到某个点，而是速度保持，根据位置公式 只需要最后一项换一下，就是纵向的速度保持公式了

\[C_{v}=k_{j} J_{t}(s(t))+k_{t} T+k_{\dot{s}}\left[\dot{s}_{1}-\dot{s}_{d}\right]^{2} \]

在时间\(t_0\)初始位置：\(S_0=[s_0,\dot s_0, \ddot s_0]\)，在时间\(t_1=t_0+T\)的结束状态\(S_1\)，得到的状态变化就是这样的：

\[\left[\dot{s}_{1}, \ddot{s}_{1}, T\right]_{i j}=\left[\left[\dot{s}_{d}+\Delta \dot{s}_{i}\right], 0, T_{j}\right] \text { , } \]

• 咦 上面的横向也是jerk呀，那不 就 没 啥 区别了嘛？ emmm

  jerk的对象不一样，一个是jerk 位置，一个是jerk 速度

• 前车加速度保持不变的操作有点学术了 不过10年的方法嘛 正常

结合纵向和横向

最后，我们需要满足的最小化的cost就是由纵向和横向给出响应权重后的求和：

\[C_{tot}=k_{lat}C_{lat}+k_{lon}C_{lon} \]

注意，对于每一步我们都使用一个新的参考作为center line，也就是说每一次的初始化/变换车道/在低速和高速间切换，我们需要将现在的重点投影到新的center line上

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9vPcVYYJ-1625538790176)(%5BFrenet%5D%20Optimal%20Trajectory%20Generation%20c1760b481c6d43e0ba976cca452668e3/Untitled%207.png)]

• 这里的每一步是指每一次的整体运行吧，一旦定好center line后只有到达了终点才需要重新再选吧 → 不是

代码示意

整体简述

1. 指定几个路径点的xy坐标和障碍物的坐标

2. 然后通过2D cubic spline生成顺滑的曲线，此时保存的[x, y, yaw, k] xy是坐标，yaw是朝向，k是曲率

   生成方式是，从xy到frenet然后再用四次多项式生成result → 后面发现这个主要是生成给显示笛卡尔用的result

   result = self.a[i] + self.b[i] * dx + self.c[i] * dx ** 2.0 + self.d[i] * dx ** 3.0
   

   但是还是生成了纵向的s的累加项的只是对象，可能再后面调用吧

3. 初始化车辆状态，速度，横向位置，横向速度，横向加速度

4. 循环仿真时间内LOOP，做frenet最优规划，

   1. 计算frenet路径
   2. 计算全局路径
   3. 检查是否与障碍物相碰
   4. 选出最小的cost对应的路径

接着我们走到每个小步的细节处理：

1. 计算frenet路径

---

1. 这里有采样空间的说法，首先是道路宽度大小，然后是采样长度：

   # generate path to each offset goal
   for di in np.arange(-MAX_ROAD_WIDTH, MAX_ROAD_WIDTH, D_ROAD_W):
   

2. 然后是横向motion planning循环时间T，在这之中有纵向的循环线，首先是最小的预测时间，最大预测时间，时间间隔

   # Lateral motion planning
   for Ti in np.arange(MIN_T, MAX_T, DT):
   

3. 循环内增加五次多项式的东西，首先是时间上的(0,Ti)以DT为间隔的时间列表

   • 横向的是五次多项式，因为只考虑一个方向，所以此时其实是一维的公式，解释在代码中clone下来有ipynb版的解释 此处引入于那边

     输入的是输出状态：

     # initial state
     c_speed = 10.0 / 3.6  # current speed [m/s]
     c_d = 2.0  # current lateral position [m]
     c_d_d = 0.0  # current lateral speed [m/s]
     c_d_dd = 0.0  # current lateral acceleration [m/s]
     

     首先我们假设在 \(x(t)\) 是指在时间t ，轨迹按五次多项式应该长这样（注意只考虑横向 只有一维）

     \[x(t) = a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5 \tag{1} \]

     • 然后在开始的状态是都是0嘛或者是初始点:

       \[x(0) = a_0 = x_s \tag{2} \]
       \[x'(t) = a_1+2a_2t+3a_3t^2+4a_4t^3+5a_5t^4 \tag{3}\]
       \[x'(0) = a_1 = v_s \tag{4} \]
       \[x''(t) = 2a_2+6a_3t+12a_4t^2 \tag{5} \]
       \[x''(0) = 2a_2 = a_s\tag{6} \]

     最后当求解系数时，我们就有以下的的公式：

     \[\begin{aligned} x(T)=a_0+a_1T+a_2T^2+a_3T^3+a_4T^4+a_5T^5&=x_e\\ x'(T)=a_1+2a_2T+3a_3T^2+4a_4T^3+5a_5T^4&=v_e\\ x''(T)=2a_2+6a_3T+12a_4T^2+20a_5T^3&=a_e\\ \end{aligned}\]

     其中根据初始状态信息我们已知以下系数

     a0 = c_d         # current lateral position [m]
     a1 = c_d_d       # current lateral speed [m/s]
     a2 = c_d_dd/ 2.0 # current lateral acceleration [m/s]
     

     剩余的转成矩阵求解就是里面的计算是按着这个

     \[\begin{bmatrix} T^3 & T^4 & T^5 \\ 3T^2 & 4T^3 & 5T^4 \\ 6T & 12T^2 & 20T^3 \end{bmatrix}\begin{bmatrix} a_3\\ a_4\\ a_5\end{bmatrix}=\begin{bmatrix} x_e-x_s-v_sT-0.5a_sT^2\\ v_e-v_s-a_sT\\ a_e-a_s\end{bmatrix} \]

     那么接下再返回横向的各种计算就比较明显了，毕竟五次多项式的系数都有了

     fp.t = [t for t in np.arange(0.0, Ti, DT)]
     fp.d = [lat_qp.calc_point(t) for t in fp.t]
     fp.d_d = [lat_qp.calc_first_derivative(t) for t in fp.t]
     fp.d_dd = [lat_qp.calc_second_derivative(t) for t in fp.t]
     fp.d_ddd = [lat_qp.calc_third_derivative(t) for t in fp.t]
     

   • 纵向的是四次多项式，主要是保证速度跟随，循环次数是根据设定的速度等

     TARGET_SPEED = 30.0 / 3.6  # target speed [m/s]
     D_T_S = 5.0 / 3.6  # target speed sampling length [m/s]
     N_S_SAMPLE = 1  # sampling number of target speed
     

     其中四次多项式的求解就和上面五次多项式系数求解差不多，就不做重复叙述了

     # Longitudinal motion planning (Velocity keeping)
     for tv in np.arange(TARGET_SPEED - D_T_S * N_S_SAMPLE,
                         TARGET_SPEED + D_T_S * N_S_SAMPLE, D_T_S):
         tfp = copy.deepcopy(fp)
         lon_qp = QuarticPolynomial(s0, c_speed, 0.0, tv, 0.0, Ti)
     
         tfp.s = [lon_qp.calc_point(t) for t in fp.t]
         tfp.s_d = [lon_qp.calc_first_derivative(t) for t in fp.t]
         tfp.s_dd = [lon_qp.calc_second_derivative(t) for t in fp.t]
         tfp.s_ddd = [lon_qp.calc_third_derivative(t) for t in fp.t]
     
     		Jp = sum(np.power(tfp.d_ddd, 2))  # square of jerk
         Js = sum(np.power(tfp.s_ddd, 2))  # square of jerk
     
         # square of diff from target speed
         ds = (TARGET_SPEED - tfp.s_d[-1]) ** 2
     
         tfp.cd = K_J * Jp + K_T * Ti + K_D * tfp.d[-1] ** 2
         tfp.cv = K_J * Js + K_T * Ti + K_D * ds
         tfp.cf = K_LAT * tfp.cd + K_LON * tfp.cv
     
         frenet_paths.append(tfp)
     

     后半部分呢，就是论文中讲的最小化jerk的二次方，真直接；然后代入上面提到的公式，复制到这里吧 直接对着代码非常明显，不过读论文的时候不知道原来 \(k_j, k_t, k_d\) 都是自选，虽然我记得好像是constant 常数

     \[C_{d}=k_{j} J_{t}(d(t))+k_{t} T+k_{d} d_{1}^{2} \tag{2} \]
     \[C_{v}=k_{j} J_{t}(s(t))+k_{t} T+k_{\dot{s}}\left[\dot{s}_{1}-\dot{s}_{d}\right]^{2} \]
     \[C_{tot}=k_{lat}C_{lat}+k_{lon}C_{lon} \]

所以总结来看frenet主要是五次多项式拟合生成轨迹，然后再计算每条轨迹的按公式来的cost值，自此还没有进行最优道路的选择工作

2. 计算全局路径

---

这个感觉问题不大，主要就是有了五次多项式后，得到的已经是计算了各个轨迹的cost了，然后从列表里一个个循环

这里回看发现，计算的横向距离 \(d\) 和他的小伙伴求导 都仅仅是作为cost的计算进入frenet path → 口误，后面看到原来是deepcopy了的，然后再看看后面有没有用上其他的计算

1. 循环整个列表，列表长度 210，单个叫 fp
2. 循环列表里有的s，每个fp 有20个s
3. 通过每个fp 内的s计算全局下的位置，因为以前存过路径点转换为顺滑的那个对象，然后就阿巴阿巴 说起来太复杂了 对着cubic_spline_planner.py看一下吧... 但是大概说一下主要功能是啥：

从点到spline

首先这里是几个点，然后用spline的方法画成了顺滑的线，然后呢 我们返回的就是对应s下顺滑线的那个点的xy值，然后呢 这还没完，我们还要转成frenet坐标系下的s和d

然后还计算了这个点和下一个点的yaw角和`ds`到 `fp` 里

最后是曲率两个yaw叫相减除以现在两点间的`ds`

```python
def calc_global_paths(fplist, csp):
    for fp in fplist:

        # calc global positions
        for i in range(len(fp.s)):
            ix, iy = csp.calc_position(fp.s[i])
            if ix is None:
                break
            i_yaw = csp.calc_yaw(fp.s[i])
            di = fp.d[i]
            fx = ix + di * math.cos(i_yaw + math.pi / 2.0)
            fy = iy + di * math.sin(i_yaw + math.pi / 2.0)
            fp.x.append(fx)
            fp.y.append(fy)

        # calc yaw and ds
        for i in range(len(fp.x) - 1):
            dx = fp.x[i + 1] - fp.x[i]
            dy = fp.y[i + 1] - fp.y[i]
            fp.yaw.append(math.atan2(dy, dx))
            fp.ds.append(math.hypot(dx, dy))

        fp.yaw.append(fp.yaw[-1])
        fp.ds.append(fp.ds[-1])

        # calc curvature
        for i in range(len(fp.yaw) - 1):
            fp.c.append((fp.yaw[i + 1] - fp.yaw[i]) / fp.ds[i])

    return fplist
```

3. 碰撞检测

---

emmm 这个很简单的判断 十分简单，计算现在路径里有的所有点对障碍物的坐标点进行距离计算如果小于机器人的半径则整条路径都定义为False，同时也对最大速度，最大加速度和最大曲率都有判断的。最后返回留下的都是满足条件的路径

def check_paths(fplist, ob):
    ok_ind = []
    for i, _ in enumerate(fplist):
        if any([v > MAX_SPEED for v in fplist[i].s_d]):  # Max speed check
            continue
        elif any([abs(a) > MAX_ACCEL for a in
                  fplist[i].s_dd]):  # Max accel check
            continue
        elif any([abs(c) > MAX_CURVATURE for c in
                  fplist[i].c]):  # Max curvature check
            continue
        elif not check_collision(fplist[i], ob):
            continue

        ok_ind.append(i)

    return [fplist[i] for i in ok_ind]

def check_collision(fp, ob):
    for i in range(len(ob[:, 0])):
        d = [((ix - ob[i, 0]) ** 2 + (iy - ob[i, 1]) ** 2)
             for (ix, iy) in zip(fp.x, fp.y)]

        collision = any([di <= ROBOT_RADIUS ** 2 for di in d])

        if collision:
            return False

    return True

• 咦 但是这里我... 有问题，返回fplist直接是False了还... 怎么玩 后面的计算也完全不需要了吧，而且不是按照横纵分了很多线嘛？为啥判断这一簇里有一个线上有就不算了？都是False 这样的表达有点小问题 emmm

  不好意思看岔了 显示check path然后跳到check collision

4. 选取最小的cost

---

如题，非常easy，然后再做出这个path动作，回到主循环，继续复制初始状态，循环下去 OVER

• 跳转 不过我比较好奇为啥不命名成fd fs 难道是我理解错了？

  是的 不是fd fs而是d,s一直加上center line的xy，得出d,s的笛卡尔fx, fy，其中因为yaw可以超90度，然后运用cos(x+pi/2)替代sin(x) 就可以又负轴

  

运行示例

以下为运行时的gif：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eEAYRPFH-1625538790178)(https://github.com/AtsushiSakai/PythonRoboticsGifs/raw/master/PathPlanning/FrenetOptimalTrajectory/animation.gif)]

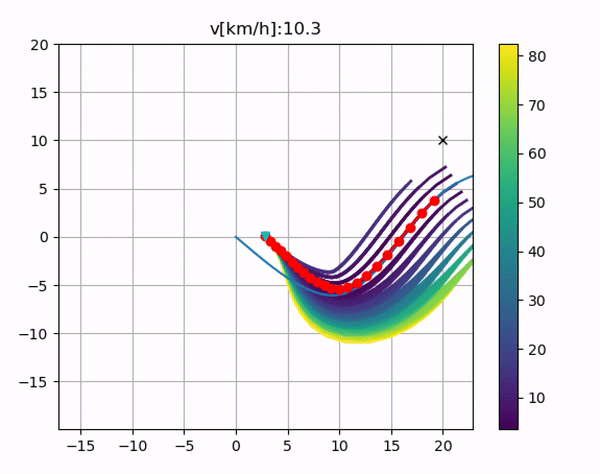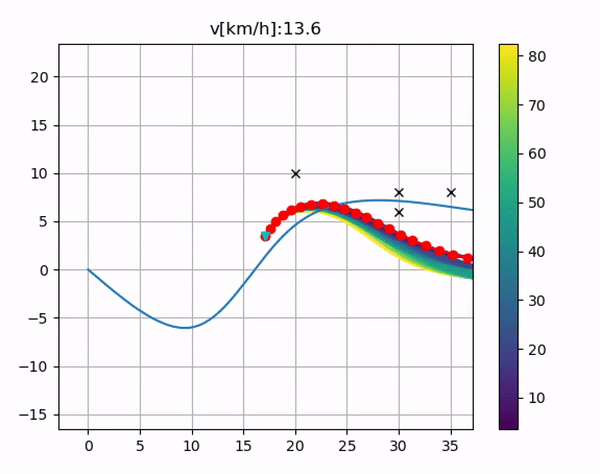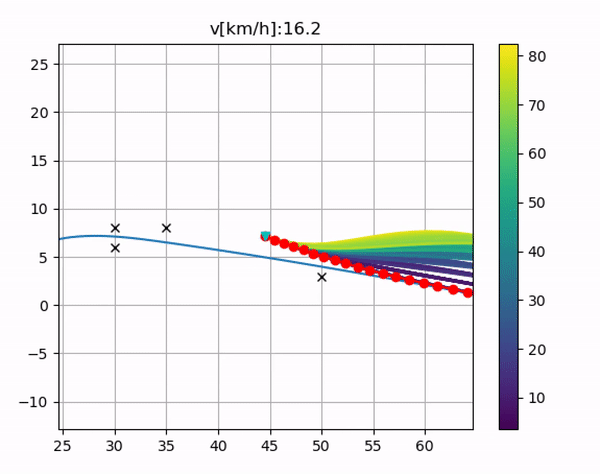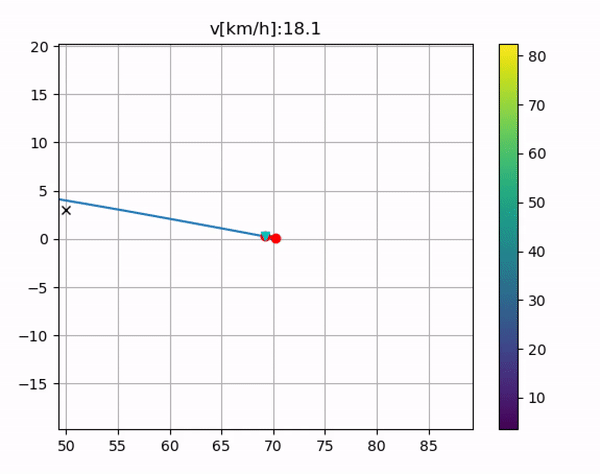
其中蓝绿色是center line，黑色x是障碍物位置，红色是预测的行驶轨迹；左边是我单独修改了画图，把所有的路线给用颜色标出来了，cost的颜色从大到小如图例所示

画图修改后的代码见此次gitee commit 点击即可跳转

总结

以上，所以生成轨迹用的是贝塞尔，然后跟随轨迹 横向距离是按五次多项式、纵向速度保持是四次多项式，然后再按论文中的cost 公式代入计算，所以理解cost公式的意义比较重要，并且各个参数的调整意味着什么。另外有一点在论文体现，代码里忽略的是关于跟随前车，超车都是假设前车加速度不变，感觉这样实际高速操作还是有安全隐患的。

对于jerk的做法，我确实没感觉出什么不妥，可能是计算速度 更新率方面需要进一步评估这个。

后面想到一个，关于实际车辆运动时的反馈，比如就算你给出了车辆运动的轨迹 甚至是那个速度，跟随问题也是需要考虑的，但是可能这就不在轨迹规划器里考虑了，而是控制跟随，比如LQR、PID、Stanley控制器等（其中LQR可能会“预习”一下，后两者 当时毕设写过了）