【论文阅读】套娃之 Blog for DMP Dynamic Movement Primitives

前言：原笔记Notion链接：https://www.notion.so/Blog-for-DMP-d34e83c05eb944ba989fc8bf9b0c0f7b 如有格式显示问题等请点击此处查看

引用

• 英文博客关于DMP的介绍：https://studywolf.wordpress.com/2013/11/16/dynamic-movement-primitives-part-1-the-basics/
  博客对应的github代码链接为：https://github.com/studywolf/pydmps
• 简书介绍：https://www.jianshu.com/p/bf5ad3fa7ff0
• 英文论文pdf：http://www-clmc.usc.edu/publications/I/ijspeert-NC2013.pdf
• 问：所以DMP是用来生成路径的吗？
  When you use a DMP what you’re doing is planning a trajectory for your real system to follow.
  答： 所以可以总结DMP的作用就是生成路径或控制信号的

If our DMP system is planning a path for the hand to follow, then what gets sent to the real system is the set of forces that need to be applied to the hand. 首先这里的举例是机械臂的

But keep in mind that the whole DMP framework is for generating a trajectory \ control signal to guide the real system. 所以可以总结DMP的作用就是生成路径或控制信号的

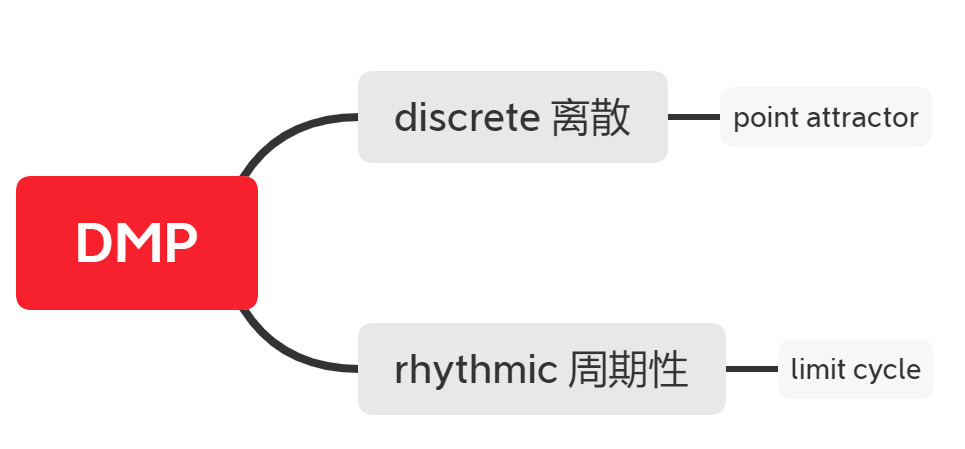
Discrete DMPs

point attractor dynamics 这个到底咋个翻译好？点到点的控制嘛？

\[\ddot{y}=\alpha_y(\beta_y(g-y)-\dot y) \tag{1} \]

其中

• \(y\)是系统状态
• \(g\)是目标
• \(\alpha\)和\(\beta\)是gain terms

可以看出是一个简单的PD控制器，再次基础上加入forcing term \(f\) 是非线性方程，怎样去定义这样一个\(f\) 也是一个难题

\[\ddot{y}=\alpha_y(\beta_y(g-y)-\dot y)+f \tag{2} \]

通过canonical dynamical system \(x\)的引入，对\(f\)的定义：

\[f(x, g)=\frac{\Sigma_{i=1}^{N} \psi_{i} w_{i}}{\Sigma_{i=1}^{N} \psi_{i}} x\left(g-y_{0}\right) \tag{3} \]

• 问：对这里引入的\(x\) 有点不太懂
  答：看后面解释\(x\)从1开始，时间越后慢慢接近0

其中

• \(y_0\)是系统的初始位置
• \(\psi_{i}\) 是given basis funciton，可以认为\(\psi_{i}\) 是\(N(c_i,h_i)\)的高斯分布，\(\psi_{i} =\text{exp}(-h_i(x-c_i)^2)\)
• \(w_i\)是\(\psi_{i}\) 的权重

所以整个\(f\)：So our forcing function is a set of Gaussians that are ‘activated’ as the canonical system \(x\) converges to its target.
Their weighted summation is normalized, and then multiplied by the \(x (g - y_0)\) term, which is both a ‘diminishing’ and spatial scaling term.

我觉得那个简书说的很有道理，\(\psi_{i}\) 是核函数，找到一组权重使得拟合误差最小【有点混合高斯的那个感觉了吼】

比如图一是各个不同的平均值的\(\psi_{i}\) ，然后不同的权重组成了图二中的weighted summation曲线

引用简书内的文字：

这里需要对(2)式作一些说明

1. \(f\)项被引入后,从现代控制系统的观点来看,相当于我们引入了一个控制项,而随着时间趋向于无穷,x会趋向于0,则控制项f也会趋向于0,整个方程还是会收敛到目标上去.

2. 从现代控制理论的观点来说,对于一个可控系统,我们能控制他到达任意状态点,但是不能控制状态的变化轨迹,状态的变化只能沿着状态空间中的向量场方向进行运动。但是对于给定的状态轨迹,我们可以学习改轨迹产生过程中的控制量(也即是学习(2)式中\(f\))，这也是为什么我上面为什么会提到学习的内容。事实上,这里的学习过程不同于现在流行的各种深度学习,它更像是一种回归过程,SVM就是一种回归.

   

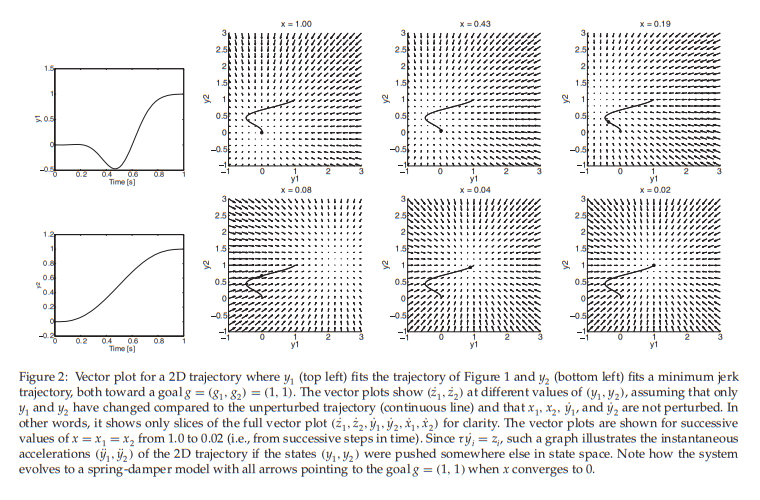
3. DMP中的运动基元这概念,笔者的认为,指的就是这里的控制项中的每一个对应的小单元.

The diminishing term

Incorporating the \(x\) term into the forcing function guarantees that the contribution of the forcing term goes to zero over time, as the canonical system does. This means that we can sleep easy at night knowing that our system can trace out some crazy path, and regardless will eventually return to its simpler point attractor dynamics and converge to the target.

也就是说引入\(x\)项 是为了保证在时间无穷处原系统会收敛

• 那为什么一定是这样子\(x\left(g-y_{0}\right)\)的形式呢？
  好像也没法写成其他形式，这样子比较简单

Spatial scaling

这一点主要是针对同样时间内goal的不同，例如

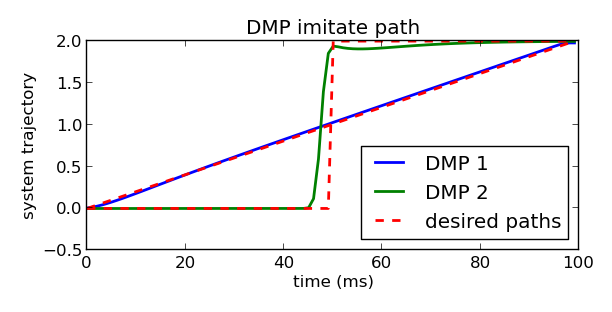
这里的同样的时间，一个goal是1，一个是2，If we don’t appropriately scale our forcing function, with the \((g - y_0)\) term, then we end up with this:

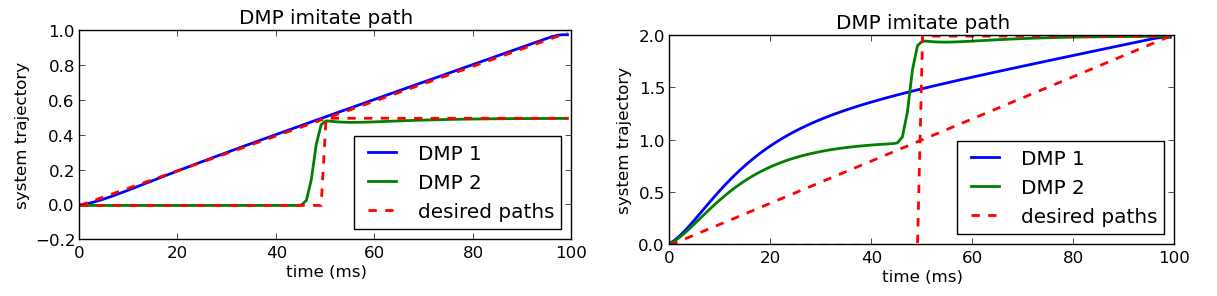
有图二的跟随轨迹的原因是，对于其他的目标点，相同的权重会使系统难以跟随期望的轨迹，所以为 \((g - y_0)\) 加入forcing function，我们就能得到

• 这里说的加入forcing function，看了一下代码的对比，感觉是整个\(f\) 方程嘛？还是说只是\(\frac{\Sigma_{i=1}^{N} \psi_{i} w_{i}}{\Sigma_{i=1}^{N} \psi_{i}} x\) 这个部分的
  按照前面第一幅图能跟随上，应该是指权重那个部分没有的话，待验证

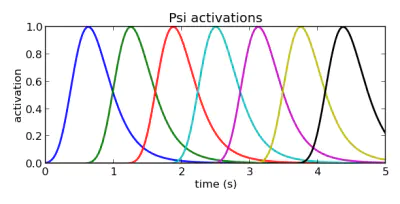
Spreading basis function centers

前情提要：\(\psi_{i}\) 是given basis funciton，可以认为\(\psi_{i}\) 是\(N(c_i,h_i)\)的高斯分布，\(\psi_{i} =\text{exp}(-h_i(x-c_i)^2)\)

现在我们的basis function \(\psi_{i}\) 是基于\(x\) 的，而\(x\) 是随时间作指数衰减的，当我们把basis function按照\(x\) 的分布来分布的时候就会出现：对于当时时间下的x，basis function长的样子 分布 更倾向于图中所示那样，而不是均匀的分布，这样对于我们在后半段时间内的拟合效果可能会很差

• 这里不知道是不是这样的理解方式：，basis function被激活的越多，越到后面越慢了
  继续看了看是这样的理解【分布会被时间所决定】

所以我们想要的分布是第二幅图的按时间均匀贴片，但是又不能丢弃\(x\) 不然就会出现上面说的Spatial scaling的情况，Additionally, we need to worry a bit about the width of each of the Gaussians, because those activated later will be activated for longer periods of time. To even it out the later basis function widths should be smaller. Through the very nonanalytical method of trial and error I’ve come to calculate the variance as

\[h_i=\frac{\#BFs}{c_i} \]

也就是把第\(i\) 个basis function的方差改成 basis function的数量除以对应第\(i\) 个basis function的平均值，经过这样的处理后，我们就能得到按照时间均匀分布的核函数也就是basis function了

• 这里对于方差的处理比较奇怪，方差原始的公式其实是：\(\sigma_i^2=\frac{(x_1-c_i)^2+\dots+(x_n-c_i)^2}{n}\)，其中的n是整个使用这个核函数的个数，如果直接改成 \(h_i=\frac{\#BFs}{c_i}\)就直接丧失了方差原本的含义了呀？那分布也不是看偏离值了？\(h_i=\frac{1}{2\sigma^2}\)
  但是仅看原因和处理结果的话，理解起来比较方便，就是看第一幅左图可知他们的width不一致，这是由方差决定的，注意因为这里\(c_i\)并不是每个核函数下数值的平均值

• 然后 中心点都不是按时间分布的，那是不是\(c_i\)也得改才对？
  是的，在代码中\(c_i\) 并不直接是平均值，而是\(e^{des_c}\)也就是按时间均匀分下来的

• 看了原文pdf，没有看到这个操作哎... 哎... 哎...
  应该说是没有详细说这个操作，奥好像说了在Page 22
  这里写了\(h_i=\text{equal spacing in } x(t)\)

  

# 代码中的操作
# set variance of Gaussian basis functions
# trial and error to find this spacing
self.h = np.ones(self.n_bfs) * self.n_bfs ** 1.5 / self.c / self.cs.ax
# ax float: a gain term on the dynamical system
# n_bfs int: number of basis functions per DMP

def gen_centers(self):
  """Set the centre of the Gaussian basis
  functions be spaced evenly throughout run time"""

  """x_track = self.cs.discrete_rollout()
  t = np.arange(len(x_track))*self.dt
  # choose the points in time we'd like centers to be at
  c_des = np.linspace(0, self.cs.run_time, self.n_bfs)
  self.c = np.zeros(len(c_des))
  for ii, point in enumerate(c_des):
      diff = abs(t - point)
      self.c[ii] = x_track[np.where(diff == min(diff))[0][0]]"""

  # desired activations throughout time
  des_c = np.linspace(0, self.cs.run_time, self.n_bfs)

  self.c = np.ones(len(des_c))
  for n in range(len(des_c)):
      # finding x for desired times t
      self.c[n] = np.exp(-self.cs.ax * des_c[n])

Temporal scaling

Spatial scaling we discussed above, 也就是上面强调forcing function的作用的
in the temporal case we’d like to be able to follow this same trajectory at different speeds. Sometimes quick, sometimes slow, but always tracing out the same path. 然后现在我们还想实现相同轨迹赋予不同的速度
To do that we’re going to add another term to our system dynamics, \(\tau\), our temporal scaling term. Given that our system dynamics are: 所以需要再次引入一个参数去控制，首先我们的系统动力学是：

\[\begin{array}{c}\ddot{y}=\alpha_{y}\left(\beta_{y}(g-y)-\dot{y}\right)+f, \\\dot{x}=-\alpha_{x} x,\end{array} \]

然后对于速度与加速度间加入\(\tau\)，这样的话如果想降速就设\(\tau\) 在(0,1)之间，加速的话就设到1以上

\[\begin{array}{l}\dot{y}+=\tau \ddot{y}, \\y+=\tau \dot{y}, \\x+=\tau \dot{x},\end{array} \]

注意这一点在原文pdf中其实是分了两个一阶公式，然后\(\tau\) 在右边，前文引用的英文博客中提到了：

\[\begin{array}{l}\tau \dot{z}=\alpha_{z} \beta_{z}\left(\left(g+\frac{f}{\alpha_{z} \beta_{z}}\right)-y\right)-\alpha_{z} z=\alpha_{z} \beta_{z}(u-y)-\alpha_{z} z\\\tau \dot{y}=z\end{array} \tag{2.8} \]

First, I didn’t see a reason to reduce the second order systems to two first order systems. When working through it I found it more confusing than helpful, so I left the dynamics as a second order systems.

Imitating a desired path 权重\(w\)

我们再看一下之前的\(f\) 其中\(\psi_{i}, x, g, y_0\)我们都已经说明了，那么\(w\)是怎么得到的呢？，其中就是根据公式(2)推出\(f\) 再求\(w\)

\[f(x, g)=\frac{\Sigma_{i=1}^{N} \psi_{i} w_{i}}{\Sigma_{i=1}^{N} \psi_{i}} x\left(g-y_{0}\right) \tag{3} \]

首先公式(2)写为：

\[f=\ddot{y} - \alpha_y(\beta_y(g-y)-\dot y) \]

然后再求里面的求得\(\ddot y\)

\[\ddot{\mathbf{y}}_{d}=\frac{\partial}{\partial t} \dot{\mathbf{y}}_{d}=\frac{\partial}{\partial t} \frac{\partial}{\partial t} \mathbf{y}_{d} \]

the weights over our basis functions such that the forcing function matches the desired trajectory \(\textbf{f}_{target}\)，然后我们的\(\textbf{f}_{d}\)是由高斯拟合出的，也就是求误差最小情况下的\(w_i\)

\[w_{i}=\underset{w_{i}}{\operatorname{argmin}} \sum_{t}\left(f\left(x_{(t)}\right)-f_{d}(t)\right)^{2} \]

带回公式(3) 也就是：

\[\Sigma_{t} \psi_{i}(t)\left(f_{target}(t)-w_{i}\left(x(t)\left(g-y_{0}\right)\right)\right)^{2} \]

然后求解的答案为：

\[w_i = \frac{\textbf{s}^T \pmb{\psi}_i \textbf{f}_{target}}{\textbf{s}^T \pmb{\psi}_i \textbf{s}} \]

其中：

\[\textbf{s} = \left( \begin{array}{c}x_{t_0}(g - y_0) \\ \vdots \\ x_{t_N}(g - y_0) \end{array} \right), \;\;\; \pmb{\psi}_i = \left( \begin{array}{ccc} \psi_i(t_0) & \dots & 0 \\ 0 & \ddots & 0 \\ 0 & \dots & \psi_i(t_n) \end{array} \right) \]

对于求\(f_{target}\)的代码：

path = np.zeros((self.n_dmps, self.timesteps))
x = np.linspace(0, self.cs.run_time, y_des.shape[1])
for d in range(self.n_dmps):
    path_gen = scipy.interpolate.interp1d(x, y_des[d])
    for t in range(self.timesteps):
        path[d, t] = path_gen(t * self.dt)
y_des = path

# calculate velocity of y_des with central differences
dy_des = np.gradient(y_des, axis=1) / self.dt

# calculate acceleration of y_des with central differences
ddy_des = np.gradient(dy_des, axis=1) / self.dt

f_target = np.zeros((y_des.shape[1], self.n_dmps))
# find the force required to move along this trajectory
for d in range(self.n_dmps):
    f_target[:, d] = ddy_des[d] - self.ay[d] * (
        self.by[d] * (self.goal[d] - y_des[d]) - dy_des[d]
    )
self.gen_weights(f_target)

求出最佳的权重：

def gen_weights(self, f_target):
        """Generate a set of weights over the basis functions such
        that the target forcing term trajectory is matched.

        f_target np.array: the desired forcing term trajectory
        """

        # calculate x and psi
        x_track = self.cs.rollout()
        psi_track = self.gen_psi(x_track)

        # efficiently calculate BF weights using weighted linear regression
        self.w = np.zeros((self.n_dmps, self.n_bfs))
        for d in range(self.n_dmps):
            # spatial scaling term
            k = self.goal[d] - self.y0[d]
            for b in range(self.n_bfs):
                numer = np.sum(x_track * psi_track[:, b] * f_target[:, d])
                denom = np.sum(x_track ** 2 * psi_track[:, b])
                self.w[d, b] = numer / denom
                if abs(k) > 1e-5:
                    self.w[d, b] /= k

        self.w = np.nan_to_num(self.w)

总结

1. The strength of the DMP framework is that the trajectory is a dynamical system.
2. DMP的作用就是生成路径或控制信号的
3. 遵循基本的运动学规律
4. 那就是采用该系统过程的DMP算法保证了最后必然会收敛到目标点.但是,需要说明的是,我们要求的不仅是能够到达指定的目标点,而且要在整个运动过程中尽可能的模仿原始轨迹的运动.

【自言自语：但是这个很难在无人驾驶的规划控制层用学习来跑，因为你模仿的不是轨迹，而是为什么轨迹是这样的感觉，所以】

---

后续可以关于DMP添加了障碍物的动力学信息以实现避障：

英文博客：https://studywolf.wordpress.com/2016/05/13/dynamic-movement-primitives-part-4-avoiding-obstacles/

原文论文Pdf: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.500.8026&rep=rep1&type=pdf

在(2)式基础上，添加了

\[\ddot{y}=\alpha_y(\beta_y(g-y)-\dot y)+f+p(y,\dot y) \]

其中，\(p(y,\dot y)\)就是用来实现避障的，具体的函数呢通过下面的推导得出：

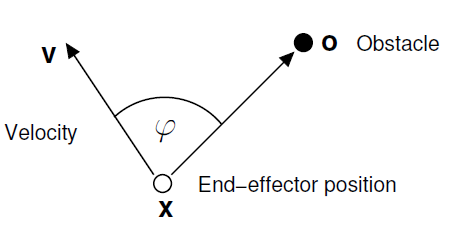
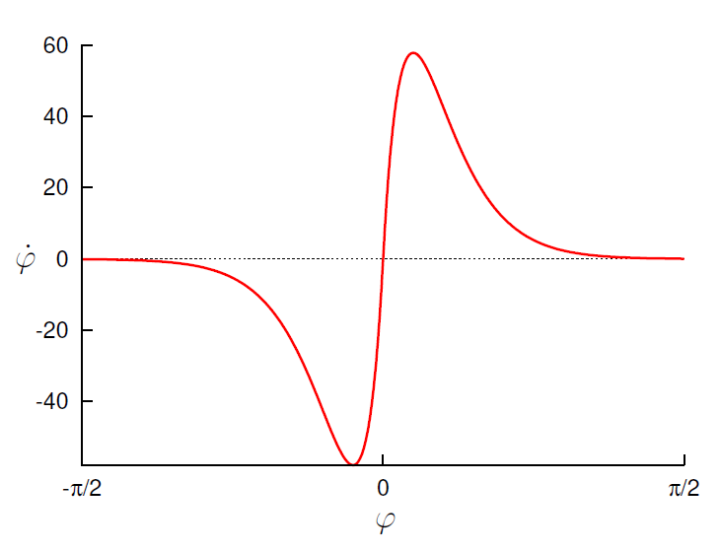
大致想法是当前速度方向与障碍物的夹角\(\varphi\)，当给出夹角时，we want to specify how much to change our steering direction, \(\dot{\varphi}\), as in the figure above

\[\begin{array}{l}\dot{\varphi} = \gamma \;\varphi \;\textrm{exp}(-\beta | \varphi |) \\\\ \textbf{p}(\textbf{y}, \dot{\textbf{y}}) = \textbf{R} \; \dot{\textbf{y}} \; \dot{\varphi} \end{array}\]

其中

• where \(\gamma\) and \(\beta\) are constants, which are specified as 1000 and \(\frac{20}{\pi}\) in the paper, respectively.
• \(\textbf{R}\) is the axis \((\textbf{o} - \textbf{y}) \times \dot{\textbf{y}}\) rotated 90 degrees (the \(\times\) denoting outer product here).