机器学习：7.逻辑回归实践

1.逻辑回归是怎么防止过拟合的？为什么正则化可以防止过拟合？

①逻辑回归是怎么防止过拟合的？

　　1.增加样本量，适用任何模型。

　　2.如果数据稀疏，使用L1正则，其他情况，用L2正则要好点。

　　3.通过特征选择，剔除一些不重要的特征，从而降低模型复杂度。

　　4.如果还过拟合，那就看看是否使用了过度复杂的特征构造工程，比如，某两个特征相乘/除/加等方式构造的特征，不要这样做了，保持原特征

　　5.检查业务逻辑，判断特征有效性，是否在用结果预测结果等。

★逻辑回归特有的防止过拟合方法:进行离散化处理，所有特征都离散化。

②为什么正则化可以防止过拟合？

　　过多的变量（特征），同时只有非常少的训练数据，会导致出现过度拟合的问题。而在正则化中我们将保留所有的特征变量，但是会减小特征变量的数量级。这个方法非常有效，当我们有很多特征变量时，其中每一个变量都能对预测产生一点影响。正如我们在房价预测的例子中看到的那样，我们可以有很多特征变量，其中每一个变量都是有用的，因此我们不希望把它们删掉，这就导致了正则化概念的发生。接下来我们会讨论怎样应用正则化和什么叫做正则化均值，然后将开始讨论怎样使用正则化来使学习算法正常工作，并避免过拟合。

2.用logiftic回归来进行实践操作，数据不限。

★案例1：使用逻辑回归算法预测乳腺癌的数据模型案例

实现代码如下：

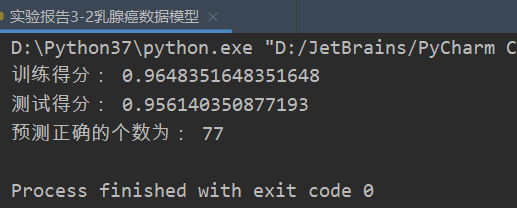
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()  # 加载乳腺癌数据
x = cancer.data  # 加载乳腺癌判别特征
y = cancer.target  # 两个特征，y=0时为阴性，y=1时为阳性
# 划分训练集与测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = \
    train_test_split(x, y, test_size=0.2)
from sklearn.linear_model import LogisticRegression
import numpy as np
model = LogisticRegression(solver='liblinear')  # 逻辑回归模型的建立
model.fit(x_train, y_train)  # 逻辑回归模型的训练
train_score = model.score(x_train, y_train)  # 训练得分
test_score = model.score(x_test, y_test)  # 测试得分
pre = model.predict(x_test)  # 预测模型
print('训练得分：', train_score, '\n测试得分：', test_score)
print('预测正确的个数为：', np.sum(pre == 1))

测试结果如下：

 ★案例2：使用逻辑回归算法预测研究生入学考试是否会被录取

数据来源：

　　链接：https://pan.baidu.com/s/1aKNslJyqozYBzkuFxdjQfw
　　提取码：2gu7

实现代码如下：

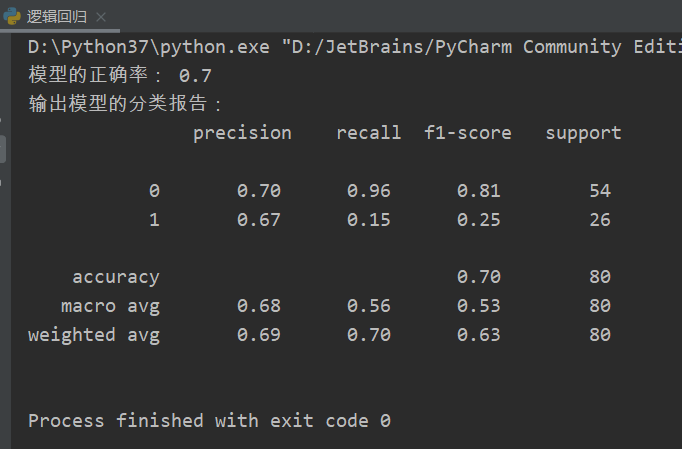
# 案例:使用逻辑回归算法预测研究生入学考试是否会被录取
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
data = pd.read_csv('../data/LogisticRegression.csv')
x = data.iloc[:, 1:]
y = data.iloc[:, 0]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=5)
# (2)构建模型
LR_model = LogisticRegression(solver='liblinear')
# (3)训练模型
LR_model.fit(x_train, y_train)
# (4)预测模型
pre = LR_model.predict(x_test)
print('模型的正确率：', LR_model.score(x_test, y_test))
print('输出模型的分类报告：\n', classification_report(y_test, pre))

测试结果如下：